Koreliacija
Statistikoje ir tikimybių teorijoje koreliacija reiškia, kaip glaudžiai susiję du duomenų rinkiniai.
Koreliacija ne visada reiškia, kad vienas veiksnys lemia kitą. Labai gali būti, kad yra ir trečias veiksnys.
Koreliacija paprastai būna vienos iš dviejų krypčių. Jos būna teigiamos arba neigiamos. Jei ji teigiama, tai du rinkiniai kyla kartu. Jei ji neigiama, tai vienas rinkinys didėja, o kitas mažėja.
Įvairiose situacijose naudojama daug skirtingų koreliacijos matavimų. Pavyzdžiui, sklaidos grafike žmonės brėžia geriausio atitikimo liniją, kad parodytų koreliacijos kryptį.
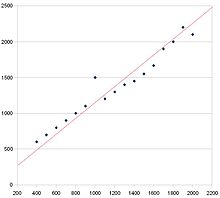
Ši sklaidos diagrama turi teigiamą koreliaciją. Tai matyti iš to, kad tendencija yra į viršų ir į dešinę. Raudona linija yra geriausio atitikimo linija.
Koreliacijos paaiškinimas
Stiprus ir silpnas - tai žodžiai, kuriais apibūdinama koreliacija. Jei koreliacija yra stipri, visi taškai yra arti vienas kito. Jei koreliacija silpna, visi taškai yra išsidėstę vienas nuo kito. Yra būdų, kaip skaičiais parodyti, kokia stipri yra koreliacija. Šie matavimai vadinami koreliacijos koeficientais. Geriausiai žinomas yra Pirsono sandaugos-momentinės koreliacijos koeficientas. Į formulę įrašykite duomenis ir gausite skaičių. Jei šis skaičius yra 1 arba -1, vadinasi, koreliacija yra stipri. Jei atsakymas yra 0, vadinasi, koreliacijos nėra. Kita koreliacijos koeficiento rūšis yra Spearmano ranginės koreliacijos koeficientas.
Koreliacija ir priežastingumas
Sąryšis ne visada reiškia, kad vienas dalykas lemia kitą (priežastinis ryšys), nes kažkas kitas galėjo lemti abu dalykus. Pavyzdžiui, karštomis dienomis žmonės perka ledus, taip pat eina į paplūdimį, kur kai kuriuos jų papjauna rykliai. Tarp ledų pardavimo ir ryklių išpuolių yra ryšys (šiuo atveju temperatūrai pakilus, abu šie rodikliai padidėja). Tačiau tai, kad ledų pardavimas padidėja, nereiškia, kad ledų pardavimas lemia (priežastinis ryšys) daugiau ryklių išpuolių arba atvirkščiai.
Kadangi koreliacija nereiškia priežastinio ryšio, mokslininkai, ekonomistai ir kt. tikrina savo teorijas kurdami izoliuotas aplinkas, kuriose keičiamas tik vienas veiksnys (jei tai įmanoma). Tačiau politikai, prekybininkai, naujienų portalai ir kiti asmenys dažnai teigia, kad tam tikra koreliacija reiškia priežastinį ryšį. Taip gali būti dėl nežinojimo arba noro įtikinti. Taip naujienų reportaže gali būti atkreiptas dėmesys į tai, kad žmonės, kurie dažniau vartoja tam tikrą produktą, turi tam tikrų sveikatos problemų, ir taip užsimenama apie priežastinį ryšį, kuris iš tikrųjų gali būti susijęs su kažkuo kitu.
Susiję puslapiai
- Cohen, J., Cohen P., West, S.G., & Aiken, L.S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences. (3rd ed.) Hillsdale, NJ: Lawrence Erlbaum Associates.
Klausimai ir atsakymai
Klausimas: Kas yra koreliacija?
A: Koreliacija - tai būdas parodyti, kaip glaudžiai susiję du duomenų rinkiniai.
K: Ar koreliacija reiškia, kad vienas duomenų rinkinys lemia kitą?
A: Ne, koreliacija ne visada reiškia, kad vienas duomenų rinkinys lemia kitą. Iš tikrųjų dažnai yra trečiasis veiksnys.
K: Kokios yra dvi koreliacijos kryptys?
A.: Dvi koreliacijos kryptys yra teigiama ir neigiama.
K: Ką reiškia teigiama koreliacija?
A: Teigiama koreliacija reiškia, kad du duomenų rinkiniai kartu didėja.
K: Ką reiškia neigiama koreliacija?
A: Neigiama koreliacija reiškia, kad vienas duomenų rinkinys didėja, o kitas mažėja.
K: Ar yra skirtingų koreliacijos matavimų?
Atsakymas: Taip, skirtingose situacijose naudojama daug skirtingų koreliacijos matavimų.
K: Kaip žmonės dažnai rodo koreliacijos kryptį sklaidos diagramoje?
A.: Norėdami parodyti koreliacijos kryptį sklaidos grafike, žmonės dažnai brėžia geriausio atitikimo liniją.
