Paralaksas
Paralaksas - tai suvokiamas objekto padėties pokytis, kai į jį žiūrima iš dviejų skirtingų vietų.
Astronomijoje metinis paralaksas yra vienintelis tiesioginis būdas išmatuoti atstumą iki žvaigždžių, esančių už Saulės sistemos ribų. Iš esmės paralaksas yra suvokiamas poslinkio reiškinys, kuris atsiranda, kai į objektą žiūrima iš skirtingų padėčių.
Jis matuojamas kampu tarp dviejų stebėjimo linijų. Artimų objektų paralaksas yra didesnis nei tolimesnių objektų, kai jie stebimi iš vienodų pozicijų, todėl paralaksas gali būti naudojamas atstumams nustatyti.
Astronomai naudoja paralakso principą atstumams iki dangaus objektų, įskaitant atstumus iki Mėnulio, Saulės ir už Saulės sistemos ribų esančių žvaigždžių, matuoti. Čia terminas "paralaksas" reiškia kampą tarp dviejų matymo linijų į žvaigždę.
Astronominiai padėties matavimai atliekami įvairiais metų laikais. Kadangi Žemės orbita tiksliai žinoma, galima nustatyti atstumą nuo padėties 1 iki padėties 2. Galima tiksliai išmatuoti kampą nuo horizonto iki objekto. Taip gaunamas trikampis, kurio bazinė linija ir kampai yra tiksliai žinomi. Iš trikampio trigonometrijos metodu apskaičiuojamas atstumas ir išreiškiamas parsekomis.
Šis metodas nepavyksta tik tada, kai objektai yra taip toli, kad Žemės orbita yra per maža, kad būtų galima tiksliai išmatuoti pakankamai didelį paralakso kampą. Toks atstumas yra apie 100 šviesmečių. Astronomai išrado įvairių būdų šiai problemai spręsti, tačiau nė vienas iš jų nėra toks tikslus, kaip paralakso metodas palyginti artimiems objektams. Tai suteikia pagrindą kosminių atstumų kopėčioms - metodams, kuriais galima apskaičiuoti didesnius atstumus.
1989-1993 m. "Hipparcos" palydovas atliko daugiau kaip 100 000 artimųjų žvaigždžių matavimus. "Gaia" (kosminis aparatas) ketina atlikti panašius maždaug milijardo žvaigždžių matavimus.
Daugelis gyvūnų, tarp jų ir žmonės, turi dvi akis, kurios suvokia gylį; tai vadinama stereopsis. Kadangi abi akys yra skirtingose galvos vietose, tai leidžia automatiškai suvokti atstumą. Tai suvokiame kaip įprastą trimatę sceną.
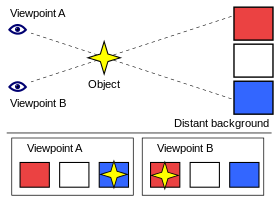
Objekto paralakso pavyzdys tolimame fone dėl vietos pasikeitimo. Žiūrint iš "Žiūrėjimo taško A", objektas atrodo esantis priešais mėlyną kvadratą. Pakeitus žiūrėjimo tašką į "Žiūrėjimo tašką B", atrodo, kad objektas persikėlė priešais raudoną kvadratą.
Klausimai ir atsakymai
K: Kas yra paralaksas?
A: Paralaksas - tai suvokiamas objekto padėties pokytis, kai objektas matomas iš dviejų skirtingų vietų. Jis matuojamas kampu tarp dviejų stebėjimo linijų ir gali būti naudojamas atstumams nustatyti.
K: Kaip paralaxas naudojamas astronomijoje?
A: Astronomijoje metinis paralaksas yra vienintelis tiesioginis būdas išmatuoti atstumą iki žvaigždžių, esančių už Saulės sistemos ribų. Astronomai naudoja paralakso principą atstumams iki dangaus objektų, įskaitant Mėnulį, Saulę ir už Saulės sistemos ribų esančias žvaigždes, matuoti.
Klausimas: Kaip apskaičiuoti atstumą naudojant paralaksą?
Atsakymas: Astronominiai padėties matavimai atliekami skirtingais metų laikais. Kadangi Žemės orbita tiksliai žinoma, galima apskaičiuoti atstumą nuo padėties 1 iki padėties 2. Galima tiksliai išmatuoti kampą nuo horizonto iki objekto, todėl gaunamas trikampis, kurio bazinė linija ir kampai yra tiksliai žinomi. Iš šio trikampio trigonometrija galima apskaičiuoti atstumus, išreikštus parsekomis.
Klausimas: Ar yra kokių nors apribojimų naudojant paralaksą tolimiems objektams matuoti?
Atsakymas: Taip, tai nepavyksta, kai objektai yra taip toli, kad Žemės orbita yra per maža, kad paralakso kampas būtų pakankamai didelis tiksliems matavimams - maždaug už 100 šviesmečių ar daugiau. Buvo išrasti kiti metodai, bet nė vienas jų nėra toks tikslus kaip paralaksas palyginti artimiems objektams matuoti.
Klausimas: Koks palydovas buvo naudojamas 1989-1993 m. artimoms žvaigždėms matuoti?
A: Šiuo laikotarpiu Hipparcos palydovu buvo išmatuota daugiau kaip 100 000 artimųjų žvaigždžių.
K: Koks kosminis aparatas atliks panašius matavimus kaip "Hipparcos"? A: Gaia (kosminis aparatas) atliks panašius maždaug milijardo žvaigždžių matavimus.
