Kreivės pritaikymas
Kreivės priderinimas - tai matematinės funkcijos, geriausiai atitinkančios duomenų taškų rinkinį, sudarymas.
Kreivės pritaikymas gali būti interpoliavimas arba išlyginimas. Naudojant interpoliavimą reikia tiksliai pritaikyti duomenis. Naudojant išlyginimą, sukuriama "lygi" funkcija, kuri apytiksliai atitinka duomenis. Susijusi tema yra regresinė analizė, kurioje daugiau dėmesio skiriama statistinės išvados klausimams, pavyzdžiui, kiek neapibrėžtumo yra kreivėje, kuri tinka duomenims, stebimiems su atsitiktinėmis paklaidomis.
Pritaikytos kreivės gali būti naudojamos duomenims vizualizuoti, funkcijos reikšmėms nuspėti, kai nėra duomenų, ir dviejų ar daugiau kintamųjų ryšiams apibendrinti. Ekstrapoliacija - tai priderintos kreivės naudojimas už stebimų duomenų intervalo ribų. Tai susiję su tam tikru neapibrėžtumu, nes ji gali atspindėti tiek kreivės sudarymo metodą, tiek ir stebimus duomenis.
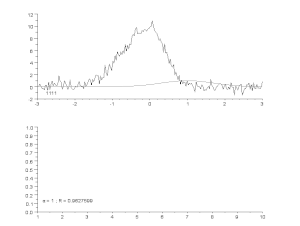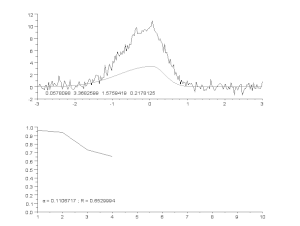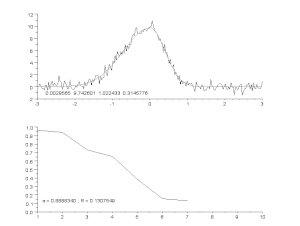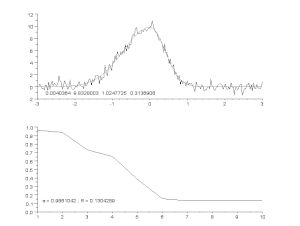
Triukšmingos kreivės pritaikymas pagal asimetrinio smailės modelio modelį, taikant iteracinį procesą (Gauso-Niutono algoritmas su kintamu slopinimo koeficientu α). Viršuje: neapdoroti duomenys ir modelis. Apačioje: normalizuotos paklaidų kvadratų sumos kitimas.
Klausimai ir atsakymai
K: Kas yra kreivės priderinimas?
A: Kreivės priderinimas - tai procesas, kurio metu sukuriama matematinė funkcija, geriausiai atitinkanti duomenų taškų rinkinį.
K.: Kokie yra du kreivių pritaikymo tipai?
A: Du kreivių pritaikymo tipai yra interpoliavimas ir išlyginimas.
K: Kas yra interpoliavimas?
A.: Interpoliavimas yra kreivės pritaikymo tipas, kai reikia tiksliai pritaikyti duomenis.
K: Kas yra išlyginimas?
A. Išlyginimas yra kreivės priderinimo būdas, kai sukuriama "lygi" funkcija, kuri apytiksliai atitinka duomenis.
K: Kas yra regresinė analizė?
A. Regresinė analizė yra susijusi tema, kurioje daugiausia dėmesio skiriama statistinės išvados klausimams, pavyzdžiui, kiek neapibrėžtumo yra kreivėje, kuri tinka duomenims, stebimiems su atsitiktinėmis paklaidomis.
K: Kokie yra kai kurie priderintų kreivių panaudojimo būdai?
A: Pritaikytos kreivės gali būti naudojamos duomenims vizualizuoti, funkcijos reikšmėms spėti, kai nėra duomenų, ir dviejų ar daugiau kintamųjų ryšiams apibendrinti.
K: Kas yra ekstrapoliacija?
A. Ekstrapoliacija - tai priderintos kreivės naudojimas už stebimų duomenų ribų. Tačiau tam tikras neapibrėžtumo laipsnis gali būti tam tikras, nes jis gali atspindėti tiek kreivės sudarymo metodą, tiek ir stebimus duomenis.
