Funkcija (matematika)
Matematikoje funkcija yra matematinis objektas, kuris duoda išvestį, kai jam suteikiama įvestis - tai gali būti skaičius, vektorius arba bet kas, kas gali egzistuoti daiktų rinkinyje.
Taigi funkcija yra tarsi mašina, kuri priima x reikšmes ir grąžina išvestį y. Visų reikšmių, kurias gali turėti x, aibė vadinama sritimi. Aibė, kurioje yra visos reikšmės, kurias gali turėti y, vadinama sritimi.
Jei taip atsitinka, sakome, kad y yra x funkcija, ir rašome y =f(x). f yra funkcijos pavadinimas ir rašome f : X → Y {\displaystyle f:X\to Y} 
(funkcija iš X į Y), norėdami išreikšti tris funkcijos dalis: sritį (x), kodinę sritį (y) ir suporavimo procesą (rodyklė).
Funkcijos pavyzdys yra f(x)=x+1. Įvestyje pateikiamas natūralusis skaičius x {\displaystyle x}
(0,1,2,3...) ir gaunamas natūralusis skaičius y {\displaystyle y} 
kuris yra x {\displaystyle x} +1 (1,2,3,4...) Funkcijos idėja buvo sukurta taip, kad apimtų įvairias galimybes. Funkcija nebūtinai turi būti lygtis. Pagrindinė idėja yra ta, kad įėjimai ir išėjimai kažkaip suporuojami, net jei procesas yra labai sudėtingas.
Metaforos
Lentelės
Įvesties ir išvesties duomenis galima surašyti į lentelę, kaip parodyta paveikslėlyje; tai lengva padaryti, jei duomenų nėra daug.
Grafikai
Paveikslėlyje matyti, kad ir 2, ir 3 buvo suporuoti su c; tai neleidžiama kita kryptimi, 2 negalėjo išvesti c ir d, kiekvienas įėjimas gali turėti tik vieną išėjimą. Visi f ( x ) {\displaystyle f(x)} 
(paveikslėlyje - c ir d) paprastai vadinami f {\displaystyle f}
vaizdų aibe, o vaizdų aibė gali būti visa kodinė sritis arba ne. Galima sakyti, kad kodinės srities A poaibis su atvaizdo aibe yra f(A). Jei įėjimai ir išėjimai turi tvarką, juos lengva nubraižyti grafike: Tokiu 
būdu atvaizdas ateis į aibės A atvaizdą. Tai leis tiek 2, tiek 3 suporuoti su neleidžiama kita kryptimi, net galima padaryti tarp kodinės srities arba ne. Galima daryti išvadą, kad kodinės aibės A poaibis yra atvaizdo aibė yra F(A).
Istorija
1690-aisiais GottfriedasLeibnizas ir Johannas Bernoulli žodį "funkcija" vartojo tarp savęs, taigi šiuolaikinė sąvoka atsirado tuo pačiu metu kaip ir skaičiuotė.
1748 m. Leonhardas Euleris pateikė: 1755 m. Euleras Euleras Euleras rašė: "Kintamojo dydžio funkcija - tai analitinė išraiška, sudaryta bet kokiu būdu iš kintamojo dydžio ir skaičių arba pastovių dydžių.", o 1755 m.: "Jei vieni dydžiai taip priklauso nuo kitų dydžių, kad, pakeitus pastaruosius, pasikeičia ir pirmieji, tai pirmieji dydžiai vadinami antrųjų funkcijomis. Šis apibrėžimas taikomas gana plačiai ir apima visus būdus, kuriais vienas dydis gali būti nulemtas kito. Taigi, jei x reiškia kintamąjį dydį, tai visi dydžiai, kurie kokiu nors būdu priklauso nuo x arba yra jo nulemti, vadinami x funkcijomis." Tai labai šiuolaikiška.
Paprastai Dirichletui priskiriama versija, kuri buvo naudojama mokyklose iki XX a. antrosios pusės: "Taip pat nesvarbu, kokiu būdu šis atitikimas nustatomas."
1939 m. Bourbaki apibendrino Dirichlet apibrėžimą ir pateikė rinkinių teorijos apibrėžimo versiją kaip atitikimą tarp įvesties ir išvesties; maždaug nuo 1960 m. tai buvo naudojama mokyklose.
Galiausiai 1970 m. Burbakis pateikė šiuolaikinį apibrėžimą kaip triple f = ( X , Y , F ) {\displaystyle f=(X,Y,F)} 
F ⊂ X × Y , ( x , f ( x ) ) ∈ F {\displaystyle F\subset X\times Y,(x,f(x))\in F}
(t. y. f : X → Y {\displaystyle f:X\į Y} ir F = { ( x , f ( x ) ) | x ∈ X , f ( x ) ∈ Y } {\displaystyle F=\{{(x,f(x))|x\in X,f(x)\in Y\}} 
).
Funkcijų tipai
- Elementariosios funkcijos - funkcijos, kurių paprastai mokomasi mokykloje: trupmenos, kvadratinės šaknys, sinuso, kosinuso ir tangento funkcijos ir kai kurios kitos funkcijos.
- Neelementinės funkcijos - Daugumoje jų nenaudojamos operacijos, kurių nesimokome mokykloje (pvz., + ar - arba galios). Daugelis integralų yra neelementarūs.
- Atvirkštinės funkcijos - funkcijos, kurios panaikina kitą funkciją. Pavyzdžiui: jei F(x) yra atvirkštinė f(x)=y, tai F(y)=x. Ne visos funkcijos turi atvirkštines funkcijas.
- Specialios funkcijos: Funkcijos, turinčios pavadinimus. Pavyzdžiui: sinusas, kosinusas ir tangentas. Tokios funkcijos kaip f(x)=3x (tris kartus x) nevadinamos specialiosiomis funkcijomis. Jos gali būti elementariosios, neelementariosios arba atvirkštinės.
Klausimai ir atsakymai
K: Kas yra funkcija matematikoje?
A: Matematikoje funkcija yra objektas, kuris, gavęs įvestį, sukuria išvestį, kuri gali būti skaičius, vektorius arba bet kas, kas gali egzistuoti daiktų aibėje.
K: Kokios yra dvi su funkcijomis susijusios aibės?
A: Visų reikšmių, kurias gali turėti x, aibė vadinama sritimi, o aibė, kurioje yra visos reikšmės, kurias gali turėti y, vadinama sritimi.
K: Kaip dažnai žymimos funkcijos?
A: Funkcijos dažnai žymimos pasvirusiomis raidėmis, pavyzdžiui, f, g, h.
K: Kaip pavaizduoti funkciją?
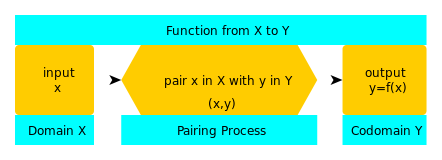
A: Funkciją vaizduojame užrašydami y = f(x), kur f yra funkcijos pavadinimas, o f : X → Y (funkcija iš X į Y) rašome norėdami parodyti tris funkcijos dalis - sritį (X), kodinę sritį (Y) ir poravimo procesą (rodyklė).
Klausimas: Ar galite pateikti funkcijos pavyzdį?
A: Funkcijos pavyzdys yra f(x) = x + 1. Kaip įvestį pateikiame natūralųjį skaičių x ir gauname natūralųjį skaičių y, kuris yra x + 1. Pavyzdžiui, jei f įvesties įrašui duodame 3, išvesties rezultatas yra 4.
K: Ar kiekviena funkcija turi būti lygtis?
Atsakymas: Ne, ne kiekviena funkcija turi būti lygtis. Pagrindinė funkcijų idėja yra ta, kad įėjimai ir išėjimai yra kaip nors suporuojami - net jei tai gali būti labai sudėtinga.
