Kas yra matematika? Apibrėžimas, pagrindinės sritys ir pritaikymas

Sužinokite, kas yra matematika: aiškus apibrėžimas, pagrindinės sritys (aritmetika, algebra, geometrija, analizė) ir praktinis pritaikymas versle, moksle ir kasdieniame gyvenime.

Autorius: Leandro Alegsa

03-02-2026 22:40

Matematika yra skaičių, formų ir modelių tyrimas. Šis žodis kilęs iš graikų kalbos žodžio μάθημα (máthema), reiškiančio "mokslą, žinias, mokymąsi", ir kartais trumpinamas į maths (Anglijoje, Australijoje, Airijoje ir Naujojoje Zelandijoje) arba math (Jungtinėse Amerikos Valstijose ir Kanadoje). Mokiniai ir jų mokyklos šiuos trumpinius dažnai vartoja aritmetikai, geometrijai ar nesudėtingai algebrai įvardyti.

Matematika apima:

Skaičiai: kaip galima suskaičiuoti daiktus.
Struktūra: kaip viskas organizuota. Ši pakraipa paprastai vadinama algebra.
Vieta: kur yra daiktai ir kaip jie išdėstyti. Ši pakraipa paprastai vadinama geometrija.
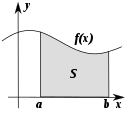
Pokyčiai: kaip dalykai tampa kitokie. Ši pakraipa paprastai vadinama analize.

Matematika yra naudinga sprendžiant realaus pasaulio problemas, todėl daugybė žmonių, be matematikų, studijuoja matematiką ir ja naudojasi. Šiandien matematikos reikia daugelyje darbų. Žmonėms, dirbantiems verslo, mokslo, inžinerijos ir statybos srityse, reikia tam tikrų matematikos žinių.

Pagrindinės matematikos sritys trumpai

Aritmetika – darbo su skaičiais pagrindai: sudėtis, atimtis, daugyba, dalyba.
Algebra – simbolių ir taisyklių sistema, leidžianti spręsti lygtis ir tirti struktūras.
Geometrija – formų, dydžių ir erdvės savybių tyrinėjimas.
Analizė (matematinė analizė) – pokyčių, ribų, funkcijų ir diferencialinių lygčių studija.
Skaičių teorija – natūralių skaičių ir jų savybių tyrimas (pvz., pirminiai skaičiai).
Topologija – erdvės formų globalios savybės, nepriklausančios nuo matmenų ar atstumų.
Matematinė logika ir teorija – formalios prielaidų, įrodymų ir formulių sistemos.
Statistika ir tikimybių teorija – duomenų analizė, neapibrėžtumo ir atsitiktinių reiškinių modeliavimas.
Diskrečioji matematika – skaičiavimai su atskirais (nesu keliamos) elementais: grafai, kombinatorika, algoritmai.
Skaitinė matematika – skaitmeniniai metodai ir kompiuterinės priemonės sprendžiant lygtis ir modelius.

Kaip matematika dirba: metodai ir sampratos

Matematika remiasi aiškiomis taisyklėmis ir loginiais įrodymais. Pagrindiniai darbo būdai yra:

Modeliavimas – realaus pasaulio reiškinių aprašymas lygtimis ir funkcijomis.
Įrodymas – loginis žingsniavimas nuo prielaidų iki išvados, užtikrinant teiginių teisingumą.
Abstrakcija – bendrų savybių išskyrimas, kad būtų galima taikyti sprendimus įvairioms situacijoms.
Skaičiavimai ir skaitmeniniai metodai – sudėtingoms problemoms spręsti naudojami numeriniai algoritmai ir kompiuteriai.

Praktiniai pritaikymai

Matematika yra pagrindas daugeliui šiuolaikinių technologijų ir mokslų. Pavyzdžiai:

Inžinerija: projektavimas, struktūrų analizė, optimizavimas.
Kompiuterių mokslas: algoritmai, kriptografija, duomenų struktūros ir mašininis mokymasis.
Finansai: rizikos vertinimas, portfelių optimizavimas, aktuariniai skaičiavimai.
Mokslas ir medicina: statistinė analizė, biostatistika, modeliavimas (pvz., ligų plitimas).
Kasdienis gyvenimas: duomenų interpretavimas, telefono navigacija, baldų išmatavimai, remontas.

Matematika mokykloje ir karjera

Mokykloje matematika moko problemų sprendimo, loginio mąstymo ir tikslumo. Šios kompetencijos yra vertingos daugelyje profesijų. Galimos karjeros kryptys, kuriose stipri matematikos bazė ypač reikalinga:

matematikas ar mokslininkas;
inžinierius;
duomenų analitikas, duomenų mokslininkas;
aktuaras;
kryptografas ar saugumo specialistas;
programuotojas ir algoritmų kūrėjas;
mokytojas ar dėstytojas.

Kodėl verta mokytis matematikos?

Matematika lavina gebėjimą mąstyti logiškai, analitiškai ir struktūriškai. Ji padeda suprasti sudėtingus reiškinius ir priimti pagrįstus sprendimus. Be to, matematika suteikia įrankius, kurie yra plačiai pritaikomi tiek kasdieniame gyvenime, tiek pažangiausiose technologijose.

Trumpa istorija ir plėtra

Matematikos ištakos siejamos su senovės civilizacijomis (pvz., Mesopotamija, Egiptas, Graikija), o vėliau ji sparčiai išsiplėtė per viduramžius ir naujųjų laikų mokslo revoliuciją. Pastaraisiais šimtmečiais matematika tapo vis labiau abstrakti, tačiau kartu ir galingesnė — atsirado naujos sritys, tokios kaip statistika, topologija ir kompiuterinė matematika.

Apibendrinant: matematika yra universali kalba, kuria aprašomi skaičiai, formos, struktūros ir pokyčiai. Ji tiek teorinė (abstrakti), tiek taikomoji (sprendžianti konkrečias problemas) — todėl yra viena pagrindinių žmogaus žinojimo sričių.

Problemų sprendimas matematikoje

Matematikoje problemos sprendžiamos pasitelkiant logiką. Vienas iš pagrindinių matematikų naudojamų logikos įrankių yra dedukcija. Dedukcija - tai specialus mąstymo būdas, kuriuo, remiantis senomis tiesomis, atrandamos ir įrodomos naujos tiesos. Matematikui priežastis, kodėl kažkas yra teisinga (vadinama įrodymu), yra tokia pat svarbi kaip ir pats faktas, kad tai yra teisinga, o ši priežastis dažnai randama naudojant dedukciją. Būtent dedukcijos naudojimas matematinį mąstymą skiria nuo kitų rūšių mokslinio mąstymo, kuris gali remtis eksperimentais arba apklausomis.

Logika ir samprotavimais matematikai naudojasi kurdami bendrąsias taisykles, kurios yra svarbi matematikos dalis. Šiose taisyklėse praleidžiama nesvarbi informacija, todėl viena taisyklė gali būti taikoma daugeliui situacijų. Ieškodama bendrųjų taisyklių, matematika vienu metu išsprendžia daugelį problemų, nes šios taisyklės gali būti panaudotos sprendžiant kitas problemas. Šios taisyklės gali būti vadinamos teoremomis (jei jos įrodytos) arba spėjimais (jei dar nežinoma, ar jos teisingos). Dauguma matematikų, norėdami rasti loginį įrodymą, naudoja neloginius ir kūrybinius samprotavimus.

Kartais matematika randa ir tiria taisykles ar idėjas, kurių dar nesuprantame. Dažnai matematikoje idėjos ir taisyklės pasirenkamos todėl, kad jos laikomos paprastomis arba tvarkingomis. Kita vertus, kartais šios idėjos ir taisyklės aptinkamos realiame pasaulyje po to, kai jos išstudijuojamos matematikoje; praeityje taip yra nutikę daugybę kartų. Apskritai matematikos taisyklių ir idėjų studijavimas gali padėti mums geriau suprasti pasaulį. Keletas matematikos uždavinių pavyzdžių: sudėties, atimties, daugybos, dalybos, skaičiavimo, trupmenų ir dešimtainių skaičių. Algebros uždaviniai sprendžiami įvertinant tam tikrus kintamuosius. Skaičiuotuvas atsako į kiekvieną matematikos uždavinį atlikdamas keturis pagrindinius aritmetinius veiksmus.

Matematikos studijų sritys

Numeris

Matematika apima skaičių ir kiekių mokslą.Tai mokslo šaka, nagrinėjanti formos, kiekio ir išdėstymo logiką. Dauguma toliau išvardytų sričių yra nagrinėjamos daugelyje skirtingų matematikos sričių, įskaitant aibių teoriją ir matematinę logiką. Skaičių teorijos studijos paprastai daugiau dėmesio skiria sveikųjų skaičių struktūrai ir elgsenai, o ne faktiniams pačių skaičių pagrindams, todėl šiame poskyryje jos nėra išvardytos.

0 , 1 , 2 , 3 , ... {\displaystyle 0,1,2,3,\ldots } $0,1,2,3,\ldots$	... , - 1 , 0 , 1 , ... {\displaystyle \ldots , -1,0,1,\ldots } $\ldots ,-1,0,1,\ldots$	1 2 , 2 3 , 0,125 , ... {\displaystyle {\frac {1}{2}},{\frac {2}{3}},0,125,\ldots } ${\frac {1}{2}},{\frac {2}{3}},0.125,\ldots$	π , e , 2 , ... {\displaystyle \pi , e,{\sqrt {2}},\ldots } $\pi ,e,{\sqrt {2}},\ldots$	1 + i , 2 e i π / 3 , ... {\displaystyle 1+i,2e^{i\pi /3},\ldots } $1+i,2e^{i\pi /3},\ldots$
Natūralūs skaičiai	Integriniai skaičiai	Racionalieji skaičiai	Realieji skaičiai	Kompleksiniai skaičiai
0 , 1 , ... , ω , ω + 1 , ... , 2 ω , ... {\displaystyle 0,1,\ldots ,\omega ,\omega ,\omega +1 ,\ldots ,2\omega ,\ldots } $0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots$	ℵ 0 , ℵ 1 , ... {\displaystyle \aleph _{0},\aleph _{1},\ldots } $\aleph _{0},\aleph _{1},\ldots$	+ , - , × , ÷ {\displaystyle +,-,\times ,\div } $+,-,\times ,\div$	> , ≥ , = , ≤ , < {\displaystyle >,\geq ,=,\leq ,< } $>,\geq ,=,\leq ,<$	f ( x ) = x {\displaystyle f(x)={\sqrt {x}}} $f(x)={\sqrt {x}}$
Eilės numeriai	Kardinalūs skaičiai	Aritmetinės operacijos	Aritmetiniai santykiai	Funkcijos

Struktūra

Daugelyje matematikos sričių nagrinėjama objekto struktūra. Dauguma šių sričių yra algebros mokslo dalis.


Skaičių teorija	Abstrakčioji algebra	Tiesinė algebra	Tvarkos teorija	Grafų teorija

Forma

Kai kuriose matematikos srityse tiriamos daiktų formos. Dauguma šių sričių yra geometrijos mokslo dalis.


Topologija	Geometrija	Trigonometrija	Diferencinė geometrija	Fraktalinė geometrija

Keisti

Kai kurios matematikos sritys tiria daiktų kaitą. Dauguma šių sričių yra analizės mokslo dalis.


Calculus	Vektorinis skaičiavimas	Analizė

Diferencialinės lygtys	Dinaminės sistemos	Chaoso teorija

Taikomoji matematika

Taikomoji matematika naudoja matematiką kitų sričių, pavyzdžiui, inžinerijos, fizikos ir kompiuterijos, problemoms spręsti.

Skaitmeninė analizė - Optimizavimas - Tikimybių teorija - Statistika - Matematiniai finansai - Žaidimų teorija - Matematinė fizika - Skysčių dinamika - Skaičiavimo algoritmai

Įžymios teoremos

Šios teoremos sudomino matematikus ir žmones, kurie nėra matematikai.

Pitagoro teorema - Paskutinioji Fermos teorema - Goldbacho spėjimas - Dvynių pirminių skaičių spėjimas - Gėdelio neužbaigtumo teoremos - Poincaré spėjimas - Kantoro įstrižainės argumentas - Keturių spalvų teorema - Zorno lema - Eulerio tapatybė - Čerčo-Turingo tezė

Tai teoremos ir spėjimai, kurie labai pakeitė matematiką.

Rymanno hipotezė - Kontinuumo hipotezė - P versus NP - Pitagoro teorema - Centrinė ribos teorema - Pagrindinė skaičiavimo teorema - Pagrindinė algebros teorema - Pagrindinė aritmetikos teorema - Pagrindinė projekcinės geometrijos teorema - Paviršių klasifikacijos teoremos - Gauso-Boneto teorema - Paskutinė Fermat teorema - Kantorovičiaus teorema

Pagrindai ir metodai

Pažanga, padaryta siekiant suprasti matematikos prigimtį, taip pat daro įtaką matematikų mokymosi būdui.

Matematikos filosofija - Matematinis intuicionizmas - Matematinis konstruktyvizmas - Matematikos pagrindai - Rinkinių teorija - Simbolinė logika - Modelių teorija - Kategorijų teorija - Logika - Atvirkštinė matematika - Matematinių simbolių lentelė

Istorija ir matematikų pasaulis

Matematika istorijoje ir matematikos istorija.

Matematikos istorija - Matematikos laiko juosta - Matematikai - Fieldso medalis - Abelio premija - Tūkstantmečio premijos uždaviniai (Clay MathPrize) - Tarptautinė matematikų sąjunga - Matematikos konkursai - Šoninis mąstymas - Matematika ir lytis

Apdovanojimai matematikos srityje

Matematikos srityje Nobelio premijos nėra. Už svarbius darbus matematikai gali gauti Abelio premiją ir Fieldso medalį.

Molio matematikos institutas pareiškė, kad kiekvienam, išsprendusiam vieną iš Tūkstantmečio premijos uždavinių, skirs milijoną dolerių.

Matematiniai įrankiai

Yra daugybė priemonių, kurios naudojamos matematikos darbams atlikti arba atsakymams į matematikos uždavinius rasti.

Senesni įrankiai

Abacus
Napiero kaulai, slankmatis
Liniuotė ir kompasas
Protinis skaičiavimas

Naujesni įrankiai

Skaičiuotuvai ir kompiuteriai
Programavimo kalbos
Kompiuterinės algebros sistemos (sąrašas)
Interneto trumpasis užrašas
statistinės analizės programinė įranga (pvz., SPSS).
SAS programavimo kalba
R programavimo kalba

Taip pat žr.

Moterų matematikos srityje laiko juosta
Amerikos matematikų draugija
Pramoninės ir taikomosios matematikos draugija
Matematikos genealogijos projektas
Matematikos dalyko klasifikacija

Klausimai ir atsakymai

K: Kas yra matematika?

A: Matematika - tai skaičių, formų ir modelių tyrinėjimas. Šis žodis kilęs iš graikų kalbos žodžio μάθημα (máthema), kuris reiškia "mokslas, žinios, mokymas".

K: Kokios yra pagrindinės matematikos sritys?

A: Pagrindinės matematikos sritys yra skaičiai, struktūra (algebra), vieta (geometrija) ir pokyčiai (analizė).

K: Kaip matematika naudojama realiame pasaulyje?

A: Taikomoji matematika naudinga sprendžiant realaus pasaulio problemas. Verslo, mokslo, inžinerijos ir statybos srityse dirbantys žmonės naudoja matematiką.

Klausimas: Ar yra sutrumpintas "matematikos" variantas?

Atsakymas: Taip - Britų Sandraugos šalyse jis gali būti sutrumpintas iki "maths", o Šiaurės Amerikoje - iki "math".

K: Ką reiškia žodis "matematika"?

Atsakymas: Žodis "matematika" kilęs iš graikiško žodžio μάθημα (máthema), kuris reiškia "mokslas, žinios arba mokymas".

Klausimas: Kokio pobūdžio problemų sprendimas susijęs su taikomąja matematika?

A: Taikomoji matematika apima realių problemų, su kuriomis susiduria versle, moksle, inžinerijoje ir statyboje dirbantys žmonės, sprendimą.

Ieškoti