Keturių spalvų teorema
Keturių spalvų teorema yra matematikos teorema. Ji teigia, kad bet kuriame plokščiame paviršiuje, kuriame yra regionų (žmonės juos laiko žemėlapiais), regionus galima nuspalvinti ne daugiau kaip keturiomis spalvomis. Du regionai, turintys bendrą ribą, negali būti nuspalvinti ta pačia spalva. Jie vadinami gretimais (esančiais vienas šalia kito), jei turi bendrą sienos atkarpą, o ne tik tašką.
Tai buvo pirmoji teorema, kurią įrodė kompiuteris, atlikdamas įrodymą išsekimo būdu. Įrodinėjant išbaigtumo būdu išvada nustatoma suskirsčius ją į atvejus ir kiekvieną iš jų įrodinėjant atskirai. Atvejų gali būti daug. Pavyzdžiui, pirmasis keturių spalvų teoremos įrodymas buvo įrodymas išsekimo būdu su 1 936 atvejais. Šis įrodymas buvo prieštaringai vertinamas, nes dauguma atvejų buvo tikrinami kompiuterine programa, o ne ranka. Trumpiausias šiandien žinomas keturių spalvų teoremos įrodymas vis dar turi daugiau kaip 600 atvejų.
Nors ši problema pirmą kartą buvo pateikta kaip šalių politinių žemėlapių spalvinimo problema, žemėlapių kūrėjai ja nelabai domisi. Kaip rašoma matematikos istoriko Kennetho May'aus straipsnyje (Wilson 2002, 2), "žemėlapiai, kuriuose naudojamos tik keturios spalvos, pasitaiko retai, o tuose, kuriuose jos naudojamos, paprastai reikia tik trijų. Knygose apie kartografiją ir žemėlapių kūrimo istoriją keturių spalvų savybė neminima".
Daugelį paprastesnių žemėlapių galima nuspalvinti trimis spalvomis. Ketvirtosios spalvos reikia kai kuriems žemėlapiams, pavyzdžiui, tokiems, kuriuose vieną regioną supa nelyginis skaičius kitų, kurie liečiasi vienas su kitu cikliškai. Vienas iš tokių pavyzdžių pateiktas paveikslėlyje. Penkių spalvų teorema teigia, kad žemėlapiui nuspalvinti pakanka penkių spalvų. Ji turi trumpą, elementarų įrodymą ir buvo įrodyta XIX a. pabaigoje. (Heawood 1890) Įrodyti, kad užtenka keturių spalvų, pasirodė daug sunkiau. Nuo 1852 m., kai pirmą kartą buvo iškelta keturių spalvų teorema, atsirado daug klaidingų įrodymų ir klaidingų priešpriešų.
Šiam žemėlapiui nuspalvinti nepakanka trijų spalvų.
Keturių spalvų žemėlapio pavyzdys
Tiksli problemos formuluotė
Intuityviai keturių spalvų teoremą galima suformuluoti taip: "esant bet kokiam plokštumos suskirstymui į gretimus regionus, vadinamam žemėlapiu, regionus galima nuspalvinti ne daugiau kaip keturiomis spalvomis taip, kad nė vienas iš dviejų gretimų regionų nebūtų tos pačios spalvos". Kad būtų galima teisingai išspręsti uždavinį, būtina išsiaiškinti kai kuriuos aspektus: Pirma, reikia ignoruoti visus taškus, kurie priklauso trims ar daugiau šalių. Antra, keistiems žemėlapiams su baigtinio ploto ir begalinio perimetro regionais gali prireikti daugiau nei keturių spalvų.
Teoremoje kiekviena "šalis" turi būti paprasčiausiai sujungtas regionas arba gretimas regionas. Realiame pasaulyje taip nėra: Aliaska, kaip JAV dalis, Nachičevanas, kaip Azerbaidžano dalis, ir Kaliningradas, kaip Rusijos dalis, nėra gretimos. Kadangi tam tikros šalies teritorija turi būti tos pačios spalvos, keturių spalvų gali nepakakti. Pavyzdžiui, panagrinėkite supaprastintą žemėlapį, pavyzdžiui, tokį, koks parodytas kairėje: Šiame žemėlapyje du A pažymėti regionai priklauso tai pačiai šaliai ir turi būti tos pačios spalvos. Tada šiam žemėlapiui reikia penkių spalvų, nes du A regionai kartu ribojasi su keturiais kitais regionais, kurių kiekvienas ribojasi su visais kitais. Jei A turėtų tik tris regionus, gali prireikti šešių ar daugiau spalvų. Tokiu būdu galima sudaryti žemėlapius, kuriems reikia savavališkai didelio spalvų skaičiaus. Panaši konstrukcija taikoma ir tuo atveju, jei visiems vandens telkiniams, kaip įprasta tikruose žemėlapiuose, naudojama viena spalva.
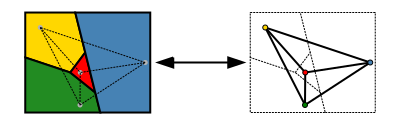
Lengviau suformuluotai teoremos versijai pasitelkiama grafų teorija. Žemėlapio regionų aibę galima abstrakčiau pavaizduoti kaip nenukreiptą grafą, kuriame yra viršūnė kiekvienam regionui ir briauna kiekvienai regionų porai, turinčiai bendrą ribinį segmentą. Šis grafas yra plokštuminis: jį galima nubrėžti plokštumoje be susikirtimų, kiekvieną viršūnę patalpinant į savavališkai pasirinktą vietą regione, kurį ji atitinka, o briaunas brėžiant kaip kreives, kurios be susikirtimų veda kiekviename regione iš viršūnės vietos į kiekvieną bendrą regiono ribos tašką. Ir atvirkščiai, tokiu būdu iš žemėlapio galima sudaryti bet kokį plokštuminį grafą. Grafų teorijos terminijoje keturių spalvų teorema teigia, kad kiekvieno planarinio grafo viršūnes galima nuspalvinti ne daugiau kaip keturiomis spalvomis taip, kad nė viena iš dviejų gretimų viršūnių nebūtų tos pačios spalvos, arba trumpai tariant, "kiekvienas planarinis grafas yra keturių spalvų" (Thomas 1998, p. 849; Wilson 2002).
Azerbaidžano žemėlapio su nesusijungiančiais regionais pavyzdys
Šio žemėlapio negalima nuspalvinti keturiomis spalvomis
Istorija
Pirmasis šią problemą 1852 m. įvardijo Francis Guthrie. Tuo metu jis studijavo teisę Anglijoje. Jis nustatė, kad Anglijos grafysčių žemėlapiui nuspalvinti reikia mažiausiai keturių spalvų. Pirmasis šią problemą aptarė Augustas de Morganas 1852 m. rugpjūčio mėn. laiške, kurį parašė Rovanui Hamlitonui. Laiške de Morganas klausia, ar tikrai pakanka keturių spalvų žemėlapiui nuspalvinti taip, kad greta esančios šalys būtų nuspalvintos skirtingomis spalvomis.
1878 m. anglų matematikas Arthuras Cayley'us šią problemą pristatė Londono matematikų draugijai. Po metų Alfredas Kempe rado tai, kas atrodė panašu į problemos įrodymą. Po vienuolikos metų, 1890 m., Percy Heawoodas įrodė, kad Alfredo įrodymas buvo klaidingas. 1880 m. Peteris Guthrie Taitas pateikė dar vieną įrodymą. Prireikė vienuolikos metų, kad būtų įrodyta, jog Taito įrodymas taip pat nepasiteisino. 1891 m. Julius Petersenas galėjo tai įrodyti. Falsifikuodamas Keilio įrodymą, Kempė taip pat parodė įrodymą uždaviniui, kurį pavadino Penkių spalvų teorema. Teorema teigia, kad bet kurį tokį žemėlapį galima nuspalvinti ne daugiau kaip penkiomis spalvomis. Egzistuoja du apribojimai: Pirma, bet kuri šalis yra gretima, nėra jokių eksklavų. Antrasis apribojimas yra tas, kad šalys turi turėti bendrą sieną; jei jos liečiasi tik taške, jas galima nuspalvinti ta pačia spalva. Nors Kempe's įrodymas buvo klaidingas, jis panaudojo kai kurias idėjas, kurios vėliau leido sukurti teisingą įrodymą.
XX a. septintajame ir aštuntajame dešimtmetyje Heinrichas Heeschas sukūrė pirmąjį kompiuterinio įrodymo eskizą. Kennethas Appelis ir Wolfgangas Hakenas šį eskizą patobulino 1976 m. (Robertson et al. 1996). Jiems pavyko sumažinti atvejų, kuriuos reikėtų patikrinti, skaičių iki 1936; vėliau buvo sukurta versija, kuri rėmėsi tik 1476 atvejų patikrinimu. Kiekvieną atvejį reikėjo išbandyti kompiuteriu (Appel ir Haken 1977).
1996 m. Neilas Robertsonas, Danielis Sandersas, Paulas Seymouras ir Robinas Thomasas patobulino metodą ir sumažino tiriamų atvejų skaičių iki 663. Vėlgi kiekvieną atvejį reikėjo patikrinti kompiuteriu.
2005 m. Georgesas Gonthier ir Benjaminas Werneris sukūrė formalų įrodymą. Tai buvo patobulinimas, nes pirmą kartą leido naudoti teoremų įrodymo programinę įrangą. Naudota programinė įranga vadinama Coq.
Keturių spalvų teorema yra pirmoji didelė matematinė problema, kuri buvo įrodyta kompiuteriu. Kadangi šio įrodymo negali atlikti žmogus, kai kurie matematikai nepripažino jo teisingu. Norint patikrinti įrodymą, reikia remtis teisingai veikiančia programine ir technine įranga, kad įrodymas būtų patvirtintas. Kadangi įrodymas buvo atliktas kompiuteriu, jis taip pat nėra labai elegantiškas.
Bandymai, kurie pasirodė klaidingi
Keturių spalvų teorema per savo ilgą istoriją buvo pagarsėjusi tuo, kad sulaukė daugybės klaidingų įrodymų ir paneigimų. Iš pradžių laikraštis "The New York Times" atsisakė pranešti apie Appelio-Hakeno įrodymą. Laikraštis taip pasielgė dėl savo politikos; jis baiminosi, kad įrodymas bus įrodytas kaip ir ankstesni klaidingi (Wilson 2002, p. 209). Kai kuriems įrodymams prireikė daug laiko, kol juos pavyko suklastoti: Kempės ir Taito įrodymų falsifikavimas užtruko daugiau nei dešimtmetį.
Paprasčiausiais pavyzdžiais paprastai stengiamasi sukurti vieną regioną, kuris liečia visus kitus. Tai priverčia likusius regionus nuspalvinti tik trimis spalvomis. Kadangi keturių spalvų teorema yra teisinga, tai visada įmanoma, tačiau žemėlapį braižantis asmuo, sutelkęs dėmesį į vieną didelį regioną, nepastebi, kad likusius regionus iš tikrųjų galima nuspalvinti trimis spalvomis.
Šį triuką galima apibendrinti: Jei kai kurių žemėlapio regionų spalvos pasirenkamos iš anksto, likusių regionų neįmanoma nuspalvinti taip, kad iš viso būtų naudojamos tik keturios spalvos. Kas nors, tikrinantis priešpriešą, gali nepagalvoti, kad gali prireikti pakeisti šių regionų spalvą. Dėl to priešpriežastis atrodys teisinga, nors taip nėra.
Galbūt vienas iš šio paplitusio klaidingo supratimo pagrindų yra tai, kad spalvos apribojimas nėra tranzityvus: regionas turi būti nuspalvintas kitaip tik nuo regionų, kuriuos jis tiesiogiai liečia, o ne nuo regionų, kurie liečia regionus, su kuriais jis liečiasi. Jei tai būtų toks apribojimas, plokštuminiams grafams reikėtų savavališkai didelio spalvų skaičiaus.
Kiti klaidingi įrodymai pažeidžia teoremos prielaidas netikėtais būdais, pavyzdžiui, naudojant regioną, kuris turi kelias nesujungtas dalis, arba neleidžiant tos pačios spalvos regionams liestis taške.
|
|
| |
| Žemėlapis (kairėje) buvo nuspalvintas penkiomis spalvomis, o norint nuspalvinti žemėlapį tik keturiomis spalvomis, reikia pakeisti bent keturis iš dešimties regionų (dešinėje). | ||
Politinių žemėlapių spalvinimas
Realiame gyvenime daugelis šalių turi eksklavų arba kolonijų. Kadangi jos priklauso šaliai, jas reikia nuspalvinti ta pačia spalva kaip ir pagrindinę šalį. Tai reiškia, kad paprastai tokiam žemėlapiui nuspalvinti reikia daugiau nei keturių spalvų. Kai matematikai kalba apie su uždaviniu susijusį grafiką, jie sako, kad jis nėra plokštuminis. Nors patikrinti, ar grafas yra plokštuminis, nesunku, rasti mažiausią skaičių spalvų, reikalingų jam nuspalvinti, yra labai sunku. Tai NP-užbaigta problema, kuri yra viena sudėtingiausių egzistuojančių problemų. Mažiausias spalvų skaičius, reikalingas grafui nuspalvinti, vadinamas jo chromatiniu skaičiumi. Daugelis problemų, kylančių bandant išspręsti keturių spalvų teoremą, yra susijusios su diskrečiąja matematika. Dėl šios priežasties dažnai naudojami algebrinės topologijos metodai.
Išplėtimas į "ne plokščius" žemėlapius
Keturių spalvų teorema reikalauja, kad "žemėlapis" būtų ant lygaus paviršiaus, kurį matematikai vadina plokštuma. 1890 m. Percy Johnas Heawoodas sukūrė tai, kas šiandien vadinama Heawoodo hipoteze: Joje keliamas tas pats klausimas, kaip ir keturių spalvų teoremoje, tačiau bet kokiam topologiniam objektui. Pavyzdžiui, torą galima nuspalvinti ne daugiau kaip septyniomis spalvomis. Heawoodo hipotezė pateikia formulę, kuri tinka visiems tokiems objektams, išskyrus Kleino butelį.
Klausimai ir atsakymai
Klausimas: Kas yra keturių spalvų teorema?
A: Keturių spalvų teorema yra matematinė teorema, teigianti, kad bet kuriame plokščiame paviršiuje, turinčiame sričių, sritis galima nuspalvinti ne daugiau kaip keturiomis spalvomis. Gretimi regionai negali būti tos pačios spalvos.
K: Kaip buvo sukurtas pirmasis keturių spalvų teoremos įrodymas?
A: Pirmasis keturių spalvų teoremos įrodymas buvo įrodymas išsekimo būdu su 1936 atvejais. Tai reiškia, kad ji buvo nustatyta padalijus ją į atvejus ir kiekvieną iš jų įrodžius atskirai.
K: Ar žemėlapių kūrėjai domisi šia problema?
Atsakymas: Ne, žemėlapių kūrėjai šia problema nelabai domisi, nes žemėlapiai, kuriuose naudojamos tik keturios spalvos, pasitaiko retai ir paprastai jiems reikia tik trijų spalvų. Knygose apie kartografiją ir žemėlapių kūrimo istoriją keturių spalvų savybė neminima.
K: Kas yra penkių spalvų teorema?
A: Penkių spalvų teorema teigia, kad žemėlapiui nuspalvinti užtenka penkių spalvų, ir turi trumpą, elementarų įrodymą, kuris buvo įrodytas XIX a. pabaigoje.
K: Kaip sunku buvo įrodyti, kad žemėlapiams nuspalvinti reikia tik 4 spalvų?
A: Įrodyti, kad žemėlapiams spalvinti reikia tik 4 spalvų, pasirodė daug sunkiau, nei tikėtasi, nes nuo pirmojo teiginio 1852 m. pasirodė daug klaidingų įrodymų ir klaidingų priešpriešų.
Klausimas: Ar yra žemėlapio pavyzdys, kuriame, norint tinkamai nuspalvinti visus regionus, reikėtų 5 ar daugiau spalvų?
Atsakymas: Taip, vienas iš tokių pavyzdžių - kai vieną regioną supa nelyginis skaičius kitų regionų, kurie liečiasi tarpusavyje cikliškai - šiuo atveju gali prireikti 5 ar daugiau spalvų, kad būtų tinkamai nuspalvinti visi regionai.
