Pitagoro teorema (a²+b²=c²): stačiojo trikampio formulė ir įrodymai

Pitagoro teorema (a²+b²=c²) — aiškiai paaiškinta stačiojo trikampio formulė, vizualūs įrodymai, pavyzdžiai ir praktiniai uždaviniai supratimui bei taikymui.

Autorius: Leandro Alegsa

05-02-2026 22:54

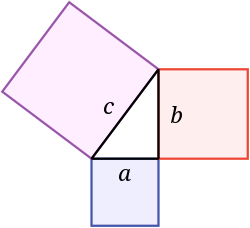
Matematikoje Pitagoro teorema arba Pitagoro teorema yra teiginys apie stačiojo trikampio kraštines.

Vienas iš stačiojo trikampio kampų visada lygus 90 laipsnių. Šis kampas yra stačiasis kampas. Dvi šalia stačiojo kampo esančios kraštinės vadinamos kojomis, o kita kraštinė - hipotenzėmis. Hipotenzė yra kraštinė, priešinga stačiajam kampui, ir ji visada yra ilgiausia kraštinė.

Pitagoro teorema teigia, kad kvadrato, esančio ant hipotenzės, plotas lygus kojų kvadratų plotų sumai. Šiame paveikslėlyje mėlynojo kvadrato plotas, pridėtas prie raudonojo kvadrato ploto, sudaro violetinio kvadrato plotą. Jis buvo pavadintas graikų matematiko Pitagoro vardu:

Jei kojų ilgiai yra a ir b, o hipotenzės ilgis yra c, tai a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} $a^{2}+b^{2}=c^{2}$ .

Yra daug įvairių šios teoremos įrodymų. Jie skirstomi į keturias kategorijas:

Trumpas paaiškinimas

Paprastai Pitagoro teorema skaitoma ir taip: stačiojo trikampio kraštinių ilgių kvadratų suma, esančių prie stačiojo kampo, lygi ilgiausios kraštinės (hipotenzės) ilgio kvadratui. Teorema galioja tik stačiąjam trikampiui.

Įrodymų kategorijos ir pavyzdžiai

Geometriniai įrodymai – naudoja plotus, panašius trikampius ar pertvarkymus. Vienas žinomiausių geometrijos įrodymų yra Euklido iš „Elementų“: jis parodo, kaip suskaidžius kvadratus ir panaudojus panašius trikampius gaunama reikiama lygybė.
Pertvarkymo (rearrangement) įrodymai – sudėjus ar perrikiavus figūras galima parodyti, kad dviejų mažesnių kvadratų plotų suma sudaro didesnio kvadrato plotą. Žymus pavyzdys – Bhaskara arba „keturi trikampukai kvadrate“ įrodymas.
Algebriniai įrodymai – veda per koordinatės, trigonometrines tapatybes arba tiesiog lygties manipuliacijas (pvz., panaudojant panašumą arba Pitagoro išvestis iš trikampio kraštinių išraiškų).
Analitiniai ir vektoriniai įrodymai – naudoja Euklido normą, skaliarinį sandaugą arba koordinatų geometriją; šie metodai ypač patogūs generalizuojant teoremą į daugiau matavų arba kitus kontekstus.

Keletas konkrečių įrodymų santraukų

Panašumų įrodymas: pažymėjus stačiojo trikampio aukštinę į hipotenzę gaunami du mažesni trikampiai, kurie abu yra panašūs vienas kitam ir pradiniam trikampiui. Iš panašumo santykių galima užrašyti proporcijas, kurios paverčiamos į a² + b² = c².
Bhaskara (pertvarkymo) pavyzdys: paimama kvadratinė figūra, kurios šone sudedami keturi vienodi stačiojo trikampiai taip, kad centre lieka mažesnis kvadratas. Du būdai išreikšti didžiojo kvadrato plotą (vienas – per visų figūrų sumą, kitas – per visų figūrų pertvarkymą) duoda teoremos formulę.
Koordinačių geometrija: statykite trikampį taip, kad viena koja būtų x ašyje (ilgis a), kita – y ašyje (ilgis b); tada hipotenzės galas turi koordinates (a, b) ir atstumas iki pradžios taško yra sqrt(a² + b²), kas iš karto duoda c = sqrt(a² + b²).

Pasekmės ir pritaikymai

Konversija: Pitagoro teoremos konversija teigia: jei trikampio kraštinių ilgiai a, b, c tenkina a² + b² = c² (su c didžiausiu), tai trikampas yra status. Tai leidžia patikrinti, ar trikampas yra status.
Pitagoro trejetai: natūralūs skaičiai (a, b, c), tenkinantys a² + b² = c², vadinami Pitagoro trejetais. Žymiausias pavyzdys yra (3, 4, 5). Visi pirminiai (primitive) trejetai gali būti išreikšti formulėmis: a = m² − n², b = 2mn, c = m² + n², kur m > n yra sveikieji be bendro daliklio ir ne abu lyginiai.
Praktiniai panaudojimai: matavimai, statyba, navigacija, kompiuterinė grafika (atstumų skaičiavimas), trigonometrinės ir fizikos taikomosios problemos.
Generalizacijos: Kosinuso teorema (lei of cosines) apima netaisyklingus trikampius: c² = a² + b² − 2ab cos(γ). Taip pat teorema generalizuojama į aukštesnes dimensijas (Euclido normos) — atstumo formulė Euklido erdvėje.

Pavyzdys

Tarkime a = 3, b = 4. Tuomet a² + b² = 9 + 16 = 25, todėl c = sqrt(25) = 5. Taigi trikampis su kraštinėmis 3, 4 ir 5 yra status.

Trumpa istorija

Pitagoro teorema žinoma jau seniai ir buvo atrasta arba naudojama įvairiose senovės civilizacijose (Babylonijoje, Indijoje, Kinijoje) dar prieš Pitagorą. Pitagoras ir jo mokiniai priskiriami teoremos sistemingam įrodymui ar populiarinimui graikų matematikoje, todėl ši teorema gavo jo vardą.

Šiame straipsnyje pateikta apžvalga apima pagrindinę teoremą, įrodymų tipus, praktinius panaudojimus ir svarbiausias pasekmes. Jei norite, galiu išsamiau parodyti konkretų įrodymą (pvz., Euklido arba Bhaskara) žingsnis po žingsnio.

Įrodymas

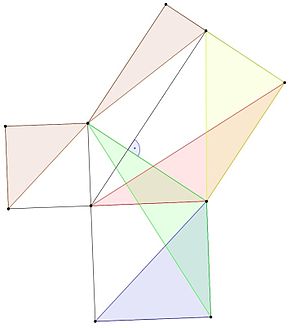
Vieną Pitagoro teoremos įrodymą rado graikų matematikas Eudoksas iš Knido.

Įrodymui naudojamos trys lemos:

Tokio paties pagrindo ir aukščio trikampiai turi tokį patį plotą.
Trikampio, kurio pagrindas ir aukštis yra tokie patys kaip kvadrato kraštinės, plotas yra lygus pusei kvadrato.
Trikampiai, kurių dvi kraštinės ir vienas kampas sutampa, yra gretutiniai ir turi tą patį plotą.

Įrodymas yra:

Mėlynojo trikampio plotas toks pat kaip ir žaliojo trikampio, nes jo pagrindas ir aukštis tokie patys (1 lema).
Žalio ir raudono trikampių dvi kraštinės lygios tų pačių kvadratų kraštinėms, o kampas lygus tiesiam kampui (90 laipsnių kampas) ir trikampio kampui, todėl jie sutampa ir turi tą patį plotą (3 lema).
Raudono ir geltono trikampių plotai yra vienodi, nes jų aukščiai ir pagrindai vienodi (1 lema).
Mėlynojo trikampio plotas lygus geltonojo trikampio plotui, nes

A b l u e = A g r e e e n = A r e d = A y e l o w {\displaystyle {\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}}={\color {yellow}A_{yellow}}}} ${\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}$

Dėl tų pačių priežasčių rudieji trikampiai yra tokio paties ploto.
Mėlyno ir rudo kvadrato plotas sudaro pusę mažesnio kvadrato ploto. Jų plotų suma lygi pusei didesnio kvadrato ploto. Dėl šios priežasties mažųjų kvadratų plotų pusės yra lygios didesniojo kvadrato ploto pusei, todėl jų plotas yra lygus didesniojo kvadrato plotui.

Įrodymas naudojant panašius trikampius

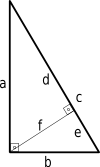
Kitą Pitagoro teoremos įrodymą galime gauti naudodami panašius trikampius.

d a = a c ⇒ d = a 2 c ( 1 ) {\displaystyle {\frac {d}{a}}={\frac {a}{c}}}\kvadratas \Rightarrow \kvadratas d={\frac {a^{2}}{c}}\kvadratas (1)} ${\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)$

e/b = b/c => e = b^2/c (2)

Iš paveikslėlio žinome, kad c = d + e {\displaystyle c=d+e\,\! } $c=d+e\,\!$ . Pakeitę (1) ir (2) lygtis:

c = a 2 c + b 2 c {\displaystyle c={\frac {a^{2}}{c}}+{\frac {b^{2}}}{c}}}} $c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}$

Dauginant iš c:

c 2 = a 2 + b 2 . {\displaystyle c^{2}=a^{2}+b^{2}\,\!. } $c^{2}=a^{2}+b^{2}\,\!.$

Pitagoro trejybės

Pitagoro trejetas arba tripletas - tai trys sveikieji skaičiai, atitinkantys lygtį a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}. $a^{2}+b^{2}=c^{2}$ .

Gerai žinomas pavyzdys - trikampis, kurio kraštinės yra 3, 4 ir 5. Jei a=3 ir b=4, tai 3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2}} $3^{2}+4^{2}=5^{2}$ , nes 9 + 16 = 25 {\displaystyle 9+16=25} $9+16=25$ . Tai taip pat galima parodyti kaip 3 2 + 4 2 = 5. {\displaystyle {\sqrt {3^{2}+4^{2}}}=5.} ${\sqrt {3^{2}+4^{2}}}=5.$

Trikampis "trys-keturi-penki" tinka visiems 3, 4 ir 5 kartotiniams. Kitaip tariant, tokie skaičiai kaip 6, 8, 10 arba 30, 40 ir 50 taip pat yra Pitagoro trikampiai. Kitas trikampio pavyzdys yra 12-5-13 trikampis, nes 12 2 + 5 2 = 13 {\displaystyle {\sqrt {12^{2}+5^{2}}}=13}} ${\sqrt {12^{2}+5^{2}}}=13$ .

Pitagoro trejybė, kuri nėra kitų trejybių kartotinė, vadinama primityviąja Pitagoro trejybe. Bet kurį primityvų Pitagoro trigubą skaičių galima rasti naudojant išraišką ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})} $(2mn,m^{2}-n^{2},m^{2}+n^{2})$ , tačiau turi būti tenkinamos šios sąlygos. Jos apriboja m {\displaystyle m} ir n {\displaystyle n} reikšmes.

m {\displaystyle m} ir n {\displaystyle n} yra teigiami sveikieji skaičiai
m {\displaystyle m} ir n {\displaystyle n} neturi bendrų veiksnių, išskyrus 1
m {\displaystyle m} ir n {\displaystyle n} turi priešingą paritetą. m {\displaystyle m} ir n {\displaystyle n} turi priešingą paritetą, kai m {\displaystyle m} yra lyginis, o n {\displaystyle n} yra nelyginis, arba m {\displaystyle m} yra nelyginis, o n {\displaystyle n} yra lyginis.
m > n {\displaystyle m>n} .

Jei tenkinamos visos keturios sąlygos, tuomet m {\displaystyle m} ir n {\displaystyle n} reikšmės sudaro primityvų Pitagoro trejetą.

m = 2 {\displaystyle m=2} $m=2$ ir n = 1 {\displaystyle n=1} $n=1$ sudaro primityvią Pitagoro trejybę. Reikšmės tenkina visas keturias sąlygas. 2 m n = 2 × 2 × 1 = 4 {\displaystyle 2mn=2\times 2\times 1=4} $2mn=2\times 2\times 1=4$ , m 2 - n 2 = 2 2 - 1 2 = 4 - 1 = 3 {\displaystyle m^{2}-n^{2}=2^{2}-1^{2}=4-1=3} $m^{2}-n^{2}=2^{2}-1^{2}=4-1=3$ ir m 2 + n 2 = 2 2 2 + 1 2 = 4 + 1 = 5 {\displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5} $m^{2}+n^{2}=2^{2}+1^{2}=4+1=5$ , todėl sukuriamas trejetas ( 3 , 4 , 5 ) {\displaystyle (3,4,5) $(3,4,5)$ }.

Klausimai ir atsakymai

K: Kas yra Pitagoro teorema?

A: Pitagoro teorema yra teiginys apie stačiojo trikampio kraštines.

K: Koks kampas stačiakampyje visada lygus 90 laipsnių?

A: Vienas iš stačiojo trikampio kampų visada yra lygus 90 laipsnių ir vadinamas stačiuoju kampu.

K: Kaip vadinamos dvi šalia stačiojo kampo esančios kraštinės?

Atsakymas: Dvi šalia stačiojo kampo esančios kraštinės vadinamos kojomis.

Klausimas: Kaip vadinama kraštinė, esanti priešais statųjį kampą?

A: Priešinga stačiajam kampui kraštinė vadinama hipotenuse ir visada yra ilgiausia kraštinė.

K: Ar yra lygtis šiai teoremai apskaičiuoti?

A: Taip, šiai teoremai apskaičiuoti yra lygtis, kuri teigia, kad "hipotenzės ilgio kvadratas lygus kitų dviejų kraštinių ilgių kvadratų sumai".

K: Ar visi trikampiai, kurių kampai yra 90 laipsnių, laikomi stačiaisiais trikampiais?

Atsakymas: Ne, ne visi trikampiai su 90 laipsnių kampais laikomi stačiaisiais trikampiais; tik tie, kurių viena kraštinė (hipotenzė) yra ilgesnė už kitas dvi kraštines ir savo gale sudaro 90 laipsnių kampą, gali būti laikomi stačiaisiais trikampiais.

Ieškoti