AlegsaOnline.com

Fraktalai: kas tai yra, savęs panašumas, pavyzdžiai ir taikymai

Sužinokite, kas yra fraktalai: savęs panašumo principas, įspūdingi pavyzdžiai ir praktiniai taikymai gamtoje, technologijose bei mene.

Autorius: Leandro Alegsa

03-02-2026

Fraktalas - tai bet koks modelis, kuris, žiūrint į jį kaip į atvaizdą, sukuria paveikslą, kurį priartinus vis dar matomas tas pats paveikslas. Jį galima supjaustyti į dalis, kurios atrodo kaip mažesnė pradinio paveikslėlio versija. Žodį fraktalas 1975 m. sukūrė Benoît Mandelbrot iš lotyniško žodžio fractus, kuris reiškia "sulaužytas" arba "sulaužytas". Paprastas pavyzdys - medis, kuris šakojasi į mažesnes šakas, o šios - į mažesnes ir t. t. Fraktalai yra ne tik gražūs, bet ir turi daug praktinio pritaikymo galimybių.

Savo panašumas (savigalimumas)

Vienas pagrindinių fraktalų bruožų yra savo panašumas (self-similarity) — tai reiškinys, kai visas objektas ir jo dalys turi panašią struktūrą. Savo panašumas būna kelių tipų:

Tikrasis (tikslus) savo panašumas: dalys yra mažesnės originalo kopijos (pavyzdžiai: Sierpińskio trikampis, Cantor'o rinkinys).
Statistinis savo panašumas: struktūra pasikartoja tik apytikriai arba tikimybiškai (gamtoje dažniau sutinkamas tipas — debesys, kranto linijos).
Quasi‑savo panašumas: panašumas pasireiškia tam tikromis mastelio savybėmis, bet formos išsamumas skiriasi.

Matematiniai pagrindai trumpai

Fraktalus galima apibrėžti įvairiais matematiniais būdais. Kai kurie svarbūs terminai ir metodai:

Iteracinės funkcijų sistemos (IFS) — skaičiavimo metodas, kuriuo gaunami daug fraktalinių formų, atliekant pasikartojančias geometrines transformacijas.
Išėjimo laiko (escape-time) fraktalai — pavyzdys: Mandelbroto ir Julia aibės, kur taškai plane klasifikuojami pagal tai, ar jų iteracijos „išsilieja“ į begalybę.
Fraktalinė (ne‑sveikųjų) matmenis — fraktalai dažnai turi ne‑sveiką, tarpinius dimensijų dydžius (pvz., 1.26 ar 1.58), kuriuos aprašo Hausdorff arba box‑counting metodai. Šis matmuo rodo, kiek smulkios struktūros užima erdvę.

Pavyzdžiai gamtoje ir matematikoje

Fraktalų pavyzdžių randame tiek gamtoje, tiek matematiniuose modeliuose:

Gamta: medžių šakos, lapai (ypač paparčio lapai), kraštovaizdžiai, upių tinklai, pakrančių linijos, debesys, romanesco brokoliai, plaučių ir kraujagyslių sistemos.
Matematika ir kompiuterių grafika: Koch‘o sniego gėlė, Sierpińskio trikampis, Cantor'o rinkinys, Mandelbroto aibė ir Julia rinkiniai.

Kaip kuriami fraktalai

Fraktalai dažnai kuriami pasikartojančiais taisyklių taikymo ciklais:

Pradedama nuo paprastos geometrinės figūros.
Taikomos transformacijos (skalavimas, pasukimas, perkėlimas) arba iteracinės taisyklės daugybei taškų.
Procesas kartojamas daug kartų — kuo daugiau iteracijų, tuo detalesnė struktūra.

Praktiniai taikymai

Fraktalai turi daug naudų įvairiose srityse:

Kompiuterinė grafika ir animacija: naudojami gamtos vaizdams (medžiai, kalnai, debesys) generuoti, taip pat kuriant tekstūras ir vizualinius efektus.
Duomenų suspaudimas: fraktaliniai metodai leidžia efektyviai koduoti vaizdus, remiantis pasikartojančiomis struktūromis.
Antennų dizainas: fraktalinės geometrinės formos suteikia plačias dažnių savybes ir kompaktišką dizainą.
Medicinos modeliavimas: kraujagyslių ar plaučių struktūrų modeliavimas, auglio formavimosi analizė.
Geologija ir ekologija: kraštovaizdžių analizė, pakrančių eroziijos ir upių tinklų modeliavimas.
Signalų apdorojimas ir analizė: fraktalinė analizė padeda suprasti sudėtingų laikinių serijų savybes (pvz., finansų rinkų, klimato duomenų).
Menas ir architektūra: fraktalinės struktūros naudojamos vizualiniam efektui ir erdvių kompozicijai kurti.

Kaip pradėti domėtis fraktais

Keletas praktinių žingsnių pradėti:

Išbandykite paprastus geometrinius fraktalus (Koch sniego gėlė, Sierpińskio trikampis) ranka ar pieštuku.
Naudokite programavimo kalbas (Python, JavaScript) su bibliotekomis, kurios leidžia kurti iteracinius fraktalus ar Mandelbroto aibę.
Skaitykite populiarius šaltinius, pvz., Benoît Mandelbrot darbą „The Fractal Geometry of Nature“ ir internetinius mokomuosius leidinius.

Fraktalai jungia matematinį tikslumą ir gamtos chaotiškumą — tai universali idėja, leidžianti paaiškinti ir modeliuoti daugelį sudėtingų formų ir procesų aplink mus.

Mandelbroto aibė yra garsus fraktalo pavyzdys.

Pavyzdžiai

Yra daugybė fraktalų rūšių, sukurtų įvairiais būdais. Vienas iš pavyzdžių yra Sierpinskio trikampis, kuriame didžiojo trikampio viduje yra begalinis skaičius mažų trikampių. Kitas pavyzdys - Mandelbroto aibė, pavadinta Benoît Mandelbrot vardu. Sierpinskio trikampis sudarytas naudojant modelius, o Mandelbroto aibė pagrįsta lygtimi.

Gamtoje taip pat yra daugybė natūralių fraktalų pavyzdžių, įskaitant medžius, snaiges, kai kurias daržoves ir pakrančių linijas.

Kocho kreivė

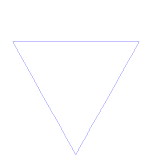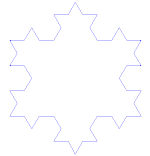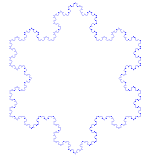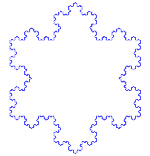
Kocho kreivė yra paprastas fraktalo pavyzdys. Pirmiausia pradėkite nuo tiesės dalies - vadinamosios tiesės atkarpos. Perpjaukite tiesę į 3 vienodo dydžio dalis. Atsikratykite tų gabalėlių vidurio ir į juos įdėkite viršutinę trikampio dalį, kurios kraštinės yra tokio pat ilgio kaip iškirpto gabalėlio. Dabar turime 4 tiesės atkarpas, kurių galai liečiasi. Tai, ką ką tik padarėme su pirmąja atkarpa, dabar galime padaryti su kiekviena iš 4 atkarpų. Dabar tą patį galime pakartoti su visomis gautomis atkarpomis. Dabar tai darysime amžinai ir pažiūrėsime, ką gausime.

Kocho kreivės ilgis yra begalybė, o Kocho kreivės plotas lygus nuliui. Tai gana keista. Tiesės atkarpos (kurios matmuo 1) ilgis gali būti 1, bet jos plotas lygus 0. Kvadrato, kurio ilgis 1, o plotis 1 (kurio matmuo 2), plotas bus 1, o ilgis - begalybė.

Panašumo matmuo

Taigi, atrodo, kad Kocho kreivė yra didesnė už kažką, kas yra 1 matmens, ir mažesnė už kažką, kas yra 2 matmens. Panašumo matmens idėja - suteikti matmenį, kuris geriau atspindėtų fraktalų ilgį arba plotą. Taigi Kocho kreivei norime dimensijos tarp 1 ir 2.

Kocho kreivę galima supjaustyti į keturias dalis, kurių kiekviena yra 1 3 {\displaystyle {\frac {1}{3}}} ${\frac {1}{3}}$ originalo dydžio. Kūrinių, į kuriuos galima supjaustyti fraktalą, skaičių vadiname N {\displaystyle N} $N$ , o dydžių skirtumą - B {\displaystyle B} $B$ . Šiuos dydžius įrašome į lygtį:

log N - log B {\displaystyle {\frac {\log N}{-\log B}}} ${\frac {\log N}{-\log B}}$

Kur log {\displaystyle \log } $\log$ yra skaičiaus logaritmas. Šis skaičius yra fraktalo Hausdorfo matmuo. Kocho kreivėje tai yra log 4 - log 1 3 = 1,2619... {\displaystyle {\frac {\log 4}{-\log {\frac {1}{3}}}}=1,2619... } ${\frac {\log 4}{-\log {\frac {1}{3}}}}=1.2619...$ , kaip ir norėjome.

Kocho kreivė yra viena paprasčiausių fraktalinių figūrų, todėl jos matmenis lengva nustatyti. Jos panašumo matmuo ir Hausdorfo matmuo yra vienodi. Tai negalioja sudėtingesniems fraktalams.

Kocho snaigė

Kocho snaigė (arba Kocho žvaigždė) yra tokia pati kaip Kocho kreivė, tik ji prasideda nuo lygiakraščio trikampio, o ne nuo tiesės atkarpos.

Naudoja

Fraktalai plačiai taikomi, pavyzdžiui, biologijoje (plaučiai, inkstai, širdies ritmo kintamumas ir t. t.), žemės drebėjimuose, finansuose, kur jie susiję su vadinamaisiais "sunkiosios uodegos" pasiskirstymais, ir fizikoje. Tai rodo, kad fraktalai turėtų būti tiriami siekiant suprasti, kodėl gamtoje fraktalai tokie dažni.

Kai kurie fraktalai egzistuoja tik meniniais sumetimais, tačiau kiti yra labai naudingi. Fraktalai yra labai efektyvios radijo antenų formos, jie naudojami kompiuterių mikroschemose, kad efektyviai sujungtų visus komponentus. Be to, pakrančių linijas galima laikyti fraktalais.

Klausimai ir atsakymai

K: Kas yra fraktalas?

A: Fraktalas - tai bet koks modelis, kuris, žiūrint į jį kaip į atvaizdą, sukuria vaizdą, kurį priartinus vaizdas išliks toks pat.

K: Kas yra atsakingas už termino "fraktalas" sukūrimą?

A: Benoît Mandelbrot 1975 m. sukūrė terminą "fraktalas".

K: Kokia yra žodžio "fraktalas" etimologija?

A: Žodis "fraktalas" kilo iš lotyniško žodžio "fractus", kuris reiškia "sulaužytas" arba "suskilęs".

K.: Ar fraktalus galima supjaustyti į dalis?

A: Taip, fraktalus galima supjaustyti į dalis, kurios atrodo kaip mažesnė pradinio paveikslo versija.

K: Ar galite pateikti fraktalo pavyzdį?

A: Paprastas fraktalo pavyzdys yra medis, kuris šakojasi į mažesnes šakas, o šios šakojasi į mažesnes šakas ir t. t.

K: Kokių praktinių pritaikymų turi fraktalai?

A.: Fraktalai turi daug praktinių pritaikymų, pavyzdžiui, kompiuterinėje grafikoje, medicinoje, fizikoje ir finansuose.

K: Kodėl fraktalai yra svarbūs?

A: Fraktalai svarbūs, nes jie gali padėti suprasti sudėtingus gamtos reiškinius ir sukurti tikslesnius modelius bei simuliacijas.