AlegsaOnline.com

Logaritmas: apibrėžimas, formulė, tipai (natūralus ir dekadinis)

Logaritmas paaiškintas aiškiai: apibrėžimas, formulės, pavyzdžiai ir skirtumai tarp natūralio (e) ir dekadinio (10) logaritmo.

Autorius: Leandro Alegsa

28-08-2025

Logaritmai arba logaritmai yra matematikos dalis. Jie susiję su eksponentinėmis funkcijomis. Logaritmas parodo, kokio eksponento (arba galios) reikia tam tikram skaičiui sudaryti, todėl logaritmai yra atvirkštinis (priešingas) eksponentiškumo principas. Istoriškai jie buvo naudingi dauginant arba dalijant didelius skaičius.

Logaritmo pavyzdys yra log 2 ( 8 ) = 3 {\displaystyle \log _{2}(8)=3\ } $\log _{2}(8)=3\$ . Šio logaritmo pagrindas yra 2, argumentas - 8, o atsakymas - 3.

Dažniausiai pasitaikantys logaritmų tipai yra paprastieji logaritmai, kurių pagrindas yra 10, ir natūralieji logaritmai, kurių pagrindas yra e ≈ 2,71828.

Apibrėžimas ir sąlygos

Matematiškai logaritmas apibrėžiamas taip: log_a(b) = c reiškia, kad a^c = b. Čia galioja svarbios sąlygos:

a > 0 (pagrindas turi būti teigiamas);
a ≠ 1 (jeigu a=1, funkcija nebūtų apibrėžta kaip įprasta);
b > 0 (argumentas turi būti teigiamas).

Pagrindinės formulės ir savybės

Atvirkštinė santykiu su laipsniu: log_a(b) = c ⇔ a^c = b.
Sandaugos formulė: log_a(xy) = log_a(x) + log_a(y).
Skirtumo formulė: log_a(x/y) = log_a(x) − log_a(y).
Galios formulė: log_a(x^k) = k · log_a(x).
Keitimosi pagrindu (change of base): log_a(b) = log_c(b) / log_c(a). Ši formulė leidžia skaičiuoti logaritmus naudojant kitą patogų pagrindą (pvz., 10 arba e).
Monotonija: jeigu a > 1, funkcija log_a(x) yra kylančia; jeigu 0 < a < 1, ji yra besileidžianti.

Dažniausiai naudojami tipai

Paprastasis (dekadinis) logaritmas: pagrindas 10, žymimas log arba log10. Pvz., log10(1000) = 3.
Natūralus logaritmas: pagrindas e ≈ 2,71828, žymimas ln. Pvz., ln(e^5) = 5.
Dvejetainis logaritmas: pagrindas 2, žymimas log2, dažnai naudojamas informatikos skaičiavimuose (bitai).

Pritaikymas ir pavyzdžiai

Logaritmai vartojami labai plačiai:

Fizikoje ir inžinerijoje — decibelų skalė (garsumo matavimas), kur svarbūs logaritminiai santykiai.
Geologijoje — Richterio skalė žemės drebėjimų stipriumui.
Kinetikoje ir chemijoje — pH skalė (hidrionų koncentracija).
Finansuose — nuolatinio augimo modeliai ir palūkanų apskaičiavimas.
Informatikoje — algoritmo sudėtingumo įvertinimai (pvz., logaritminės funkcijos).

Kelios konkrečios užduotys ir pavyzdžiai:

Jeigu turime lygtį 2^x = 10, sprendimas yra x = log_2(10) arba naudojant keitimosi pagrindu x = log10(10) / log10(2) ≈ 1 / 0,3010 ≈ 3,3219.
log10(100) = 2, nes 10^2 = 100.
ln(e^3) = 3, nes e^3 = e^3.

Skaičiavimas ir skaitmeniniai įrankiai

Anksčiau logaritmai buvo labai svarbūs rankiniams skaičiavimams ir prietaisams, kaip slankioji lentelė (slide rule). Šiandien logaritmai lengvai skaičiuojami skaičiuotuvais ir kompiuterinėmis bibliotekomis. Jeigu skaičiuotuvas turi tik ln ir log10 mygtukus, bet reikia log_a(b), galima panaudoti keitimosi pagrindu formulę:

log_a(b) = ln(b) / ln(a) = log10(b) / log10(a).

Diferencijavimas ir integravimas (trumpai)

Natūraliojo logaritmo išvestinė: d/dx[ln x] = 1/x (x>0). Tai svarbi savybė matematinėse analizėse. Integralas: ∫ ln x dx = x ln x − x + C.

Istorinė pastaba

Logaritmus XVII amžiuje išvystė John Napier kaip būdą palengvinti dauginimą ir dalijimą, vėliau juos tobulino ir plėtojo Henry Briggs (dekadinio logaritmo idėja). Logaritmai buvo esminė priemonė inžinerijoje iki skaitmeninių skaičiuotuvų eroos.

Santrauka

Logaritmai yra naudinga ir plačiai taikoma matematinė priemonė, leidžianti konvertuoti eksponentines lygtis į linijines, supaprastinti skaičiavimus ir modeliuoti reiškinius, kurie turi logaritminį pobūdį. Svarbu atsiminti pagrindines taisykles: pagrindas turi būti teigiamas ir skirtingas nuo 1, o argumentas turi būti teigiamas.

Atidarytas "Nautilus" apvalkalas. Jo kameros sudaro logaritminę spiralę

Istorija

Logaritmai pirmą kartą buvo panaudoti Indijoje II a. pr. m. e. Pirmasis naujaisiais laikais logaritmus panaudojo vokiečių matematikas Michaelis Stifelis (apie 1487-1567 m.). 1544 m. jis užrašė šias lygtis: q m q n = q m + n {\displaystyle q^{m}q^{n}=q^{m+n}} $q^{m}q^{n}=q^{m+n}$ ir q m q n = q m - n {\displaystyle {\tfrac {q^{m}}}{q^{n}}}=q^{m-n}}}. ${\tfrac {q^{m}}{q^{n}}}=q^{m-n}$ Tai yra logaritmų supratimo pagrindas. Stifeliui m {\displaystyle m} ir n {\displaystyle n} turėjo būti sveikieji skaičiai. Džonas Napjeras (1550-1617) nenorėjo šio apribojimo ir norėjo, kad eksponentams būtų nustatytas intervalas.

Pasak Napier, logaritmai išreiškia santykius: a {\displaystyle a} turi tokį patį santykį su b {\displaystyle b} $b$ , kaip ir c {\displaystyle c} $c$ su d {\displaystyle d} , $d$ jei jų logaritmų skirtumas sutampa. Matematiškai: log ( a ) - log ( b ) = log ( c ) - log ( d ) {\displaystyle \log(a)-\log(b)=\log(c)-\log(d)} $\log(a)-\log(b)=\log(c)-\log(d)$ . Iš pradžių buvo naudojamas e pagrindas (nors šis skaičius dar nebuvo pavadintas). Henris Briggsas pasiūlė logaritmų pagrindu naudoti 10, nes tokie logaritmai labai naudingi astronomijoje.

Ryšys su eksponentinėmis funkcijomis

Logaritmas parodo, kokio eksponento (arba galios) reikia tam tikram skaičiui sudaryti, todėl logaritmai yra atvirkštinis (priešingas) eksponentizavimas.

Kaip eksponentinę funkciją sudaro trys dalys, taip ir logaritmą sudaro trys dalys. Trys logaritmo dalys yra pagrindas, argumentas ir atsakymas (dar vadinamas galia).

Tai eksponentinė funkcija:

2 3 = 8 {\displaystyle 2^{3}=8\ } $2^{3}=8\$

Šioje funkcijoje pagrindas yra 2, argumentas - 3, o atsakymas - 8.

Ši eksponentinė funkcija turi atvirkštinę funkciją - logaritmą:

log 2 ( 8 ) = 3 {\displaystyle \log _{2}(8)=3\ } $\log _{2}(8)=3\$

Šio logaritmo pagrindas yra 2, argumentas - 8, o atsakymas - 3.

Skirtumas nuo šaknų

Sudėtis turi vieną atvirkštinį veiksmą - atimtį. Taip pat ir daugyba turi vieną atvirkštinį veiksmą - dalybą. Todėl gali būti sunku suprasti, kodėl daugyba iš tikrųjų turi dvi atvirkštines operacijas: Kodėl mums reikia logaritmo, jei jau yra šaknis? Taip yra todėl, kad eksponentavimas nėra komutacinis.

Tai iliustruoja šis pavyzdys:

Jei x+2=3, atimties metodu galite sužinoti, kad x=3-2. Tas pats pasakytina ir apie 2+x=3: taip pat gausite x=3-2. Taip yra todėl, kad x+2 yra tas pats, kas 2+x.
Jei turite x - 2=3, tai dalybos metodu galite sužinoti, kad x= 3 2 {\textstyle {\frac {3}{2}}} ${\textstyle {\frac {3}{2}}}$ . Tas pats yra, jei 2 - x=3: taip pat gausite x= 3 2 {\textstyle {\frac {3}{2}}} ${\textstyle {\frac {3}{2}}}$ . Taip yra todėl, kad x - 2 yra tas pats, kas 2 - x.
Jei turite x²=3, tada, norėdami sužinoti x, naudokite (kvadratinę) šaknį: Gausite rezultatą x = 3 {\textstyle {\sqrt {3}}} ${\textstyle {\sqrt {3}}}$ . Tačiau jei 2^x =3, tada šaknies šaknies naudoti negalite, kad sužinotumėte x. Veikiau turite naudoti (dvejetainį) logaritmą, kad sužinotumėte x: Gaunamas rezultatas x=log₂(3).
Taip yra todėl, kad 2 ^xpaprastai nėra tas pats, kas x ²(pavyzdžiui, 2 ⁵=32, bet 5²=25).

Naudoja

Logaritmais galima lengviau dauginti ir dalyti didelius skaičius, nes sudėti logaritmus yra tas pats, kas dauginti, o atimti logaritmus - tas pats, kas dalyti.

Prieš išpopuliarėjant ir paplitus skaičiuotuvams, žmonės daugindami ir dalydami naudojosi knygose esančiomis logaritmų lentelėmis. Tą pačią informaciją, pateiktą logaritmų lentelėje, buvo galima rasti ir slankmačiuose - įrankyje su užrašytais logaritmais.

Gamtoje dažnai pasitaiko logaritminės spiralės. Pavyzdžiai - nautilio kiautas arba saulėgrąžų sėklų išsidėstymas.
Chemijoje hidronio jonų (H₃O ⁺, H formos, kurią H ⁺įgauna vandenyje) aktyvumo logaritmo, išreikšto baziniu 10 logaritmu, neigiama reikšmė vadinama pH. Neutraliame vandenyje hidronio jonų aktyvumas yra 10 ⁻⁷mol/l, esant 25 °C temperatūrai, taigi pH yra 7. (Taip yra todėl, kad pusiausvyros konstanta, hidronio jonų ir hidroksilo jonų koncentracijos sandauga, vandens tirpaluose yra 10 ⁻¹⁴M².)
Pagal Richterio skalę žemės drebėjimo stiprumas matuojamas 10 bazių logaritminėje skalėje.
Astronomijoje regimasis dydis logaritmiškai matuoja žvaigždžių ryškumą, nes akis taip pat logaritmiškai reaguoja į ryškumą.
Muzikiniai intervalai matuojami logaritminiu būdu kaip pustoniai. Intervalas tarp dviejų natų, išreikštas semitonais, yra dažnio santykio bazės-2^1/12 logaritmas (arba 12 kartų bazės-2 logaritmas). Daliniai pustoniai naudojami nelygioms temperacijoms. Ypač nukrypimams nuo lygių temperacijų skalės matuoti intervalai taip pat išreiškiami centais (šimtosiomis lygių temperacijų pustonio dalimis). Intervalas tarp dviejų natų centais yra dažnio santykio bazės-2^1/1200 logaritmas (arba 1200 kartų bazės-2 logaritmas). MIDI sistemoje natos numeruojamos pagal pustonių skalę (logaritminis absoliutus nominalus aukštis, kai vidurinis C yra 60). Mikrotuningui su kitomis derinimo sistemomis apibrėžiama logaritminė skalė, suderinamai užpildanti intervalus tarp lygiavertės temperuotos skalės pustonių. Ši skalė atitinka natų numerius sveikiems pustoniams. (žr. mikrotuningavimą MIDI).

Bendrieji logaritmai

Logaritmai iki 10 pagrindo vadinami bendraisiais logaritmais. Jie paprastai rašomi be bazės. Pavyzdžiui:

log ( 100 ) = 2 {\displaystyle \log(100)=2\ } $\log(100)=2\$

Tai reiškia, kad:

10 2 = 100 {\displaystyle 10^{2}=100\ } $10^{2}=100\$

Natūralieji logaritmai

Logaritmai iki bazės e vadinami natūraliosiomis logaritminėmis vertėmis. Skaičius e yra beveik 2,71828, jis taip pat vadinamas Eulerio konstanta matematiko Leonardo Eulerio garbei.

Natūralieji logaritmai gali turėti simbolius log e ( x ) {\displaystyle \log _{e}(x)\,} $\log _{e}(x)\,$ arba ln ( x ) {\displaystyle \ln(x)\,} $\ln(x)\,$

Kai kurie autoriai mieliau naudoja natūraliuosius logaritmus kaip log ( x ) {\displaystyle \log(x)}, $\log(x)$ bet paprastai tai pamini įžanginiuose puslapiuose.

Bendrieji logaritmų pagrindai

bazė	santrumpa	Komentarai
2	ld {\displaystyle \operatorname {ld} } $\operatorname {ld}$	Labai paplitęs informatikos srityje (dvejetainis)
e	ln {\displaystyle \ln } $\ln$ arba tiesiog log {\displaystyle \log } $\log$	Jo pagrindas yra Eulerio konstanta e. Tai dažniausiai grynojoje matematikoje naudojamas logaritmas.
10	log 10 {\displaystyle \log _{10}} $\log _{10}$ arba log {\displaystyle \log } $\log$ (kartais taip pat rašomas kaip lg {\displaystyle \lg } $\lg$ )	Naudojamas kai kuriuose moksluose, pavyzdžiui, chemijoje ir biologijoje.
bet koks skaičius, n	log n {\displaystyle \log _{n}} $\log _{n}$	Tai yra bendras logaritmų rašymo būdas

Logaritmų savybės

Logaritmai pasižymi daugeliu savybių. Pavyzdžiui:

Savybės iš logaritmo apibrėžimo

Ši savybė tiesiogiai išplaukia iš logaritmo apibrėžimo:

log n ( n a ) = a {\displaystyle \log _{n}(n^{a})=a} $\log _{n}(n^{a})=a$ Pavyzdžiui

log 2 ( 2 3 ) = 3 {\displaystyle \log _{2}(2^{3})=3} $\log _{2}(2^{3})=3$ ir

log 2 ( 1 2 ) = - 1 {\displaystyle \log _{2}{\bigg (}{\frac {1}{2}}}{\bigg )}=-1} $\log _{2}{\bigg (}{\frac {1}{2}}{\bigg )}=-1$ , nes 1 2 = 2 - 1 {\displaystyle {\frac {1}{2}}=2^{-1}} ${\frac {1}{2}}=2^{-1}$ .

Skaičiaus a
logaritmas iki bazės b yra tas pats, kaip a logaritmas, padalytas iš b logaritmo,

log b ( a ) = log ( a ) log ( b ) {\displaystyle \log _{b}(a)={\frac {\log(a)}{\log(b)}}}} $\log _{b}(a)={\frac {\log(a)}{\log(b)}}$

Pavyzdžiui, tegul a yra 6, o b - 2. Naudodamiesi skaičiuotuvais galime parodyti, kad tai tiesa arba bent jau labai artima:

log 2 ( 6 ) = log ( 6 ) log ( 2 ) {\displaystyle \log _{2}(6)={\frac {\log(6)}{\log(2)}}}} $\log _{2}(6)={\frac {\log(6)}{\log(2)}}$

log 2 ( 6 ) ≈ 2,584962 {\displaystyle \log _{2}(6)\aprox 2,584962} $\log _{2}(6)\approx 2.584962$

2,584962 ≈ 0,778151 0,301029 ≈ 2,584970 {\displaystyle 2,584962\aprox {\frac {0,778151}{0,301029}}\aprox 2,584970} $2.584962\approx {\frac {0.778151}{0.301029}}\approx 2.584970$

Mūsų rezultatuose buvo nedidelė paklaida, tačiau ji atsirado dėl skaičių apvalinimo.

Kadangi natūralųjį logaritmą sunku įsivaizduoti, nustatome, kad, kalbant apie dešimtąjį logaritmą:

ln ( x ) = log ( x ) log ( e ) ≈ log ( x ) 0,434294 {\displaystyle \ln(x)={\frac {\log(x)}{\log(e)}}}\approx {\frac {\log(x)}{0,434294}}}}} $\ln(x)={\frac {\log(x)}{\log(e)}}\approx {\frac {\log(x)}{0.434294}}$ Kur 0,434294 yra apytikslė e logaritmo reikšmė.

Operacijos su logaritmo argumentais

Logaritmus, kurie dauginasi savo argumento viduje, galima keisti taip:

log ( a b ) = log ( a ) + log ( b ) {\displaystyle \log(ab)=\log(a)+\log(b)} $\log(ab)=\log(a)+\log(b)$

Pavyzdžiui,

log ( 1000 ) = log ( 10 ⋅ 10 ⋅ 10 ) = log ( 10 ) + log ( 10 ) + log ( 10 ) + log ( 10 ) = 1 + 1 + 1 + 1 = 3 {\displaystyle \log(1000)=\log(10\cdot 10\cdot 10)=\log(10)+\log(10)+\log(10)=1+1+1+1=3} $\log(1000)=\log(10\cdot 10\cdot 10)=\log(10)+\log(10)+\log(10)=1+1+1=3$

Tas pats galioja ir dalijimui, tačiau vietoj sudėties atliekama atimtis, nes ji yra atvirkštinis daugybos veiksmas:

log ( a b ) = log ( a ) - log ( b ) {\displaystyle \log {\bigg (}{\frac {a}{b}}{\bigg )}=\log(a)-\log(b)} $\log {\bigg (}{\frac {a}{b}}{\bigg )}=\log(a)-\log(b)$

Logaritmų lentelės, slankmačiai ir istorinės programos

Iki elektroninių kompiuterių mokslininkai kasdien naudojo logaritmus. Logaritmai padėjo mokslininkams ir inžinieriams daugelyje sričių, pavyzdžiui, astronomijoje.

Prieš kompiuterius logaritmų lentelė buvo svarbus įrankis. 1617 m. Henris Briggsas išspausdino pirmąją logaritmų lentelę. Tai buvo netrukus po pagrindinio Napiero išradimo. Vėliau žmonės kūrė geresnės apimties ir tikslumo lenteles. Šiose lentelėse buvo surašytos log_b(x) ir b reikšmės ^xbet kokiam skaičiui x tam tikrame intervale, tam tikru tikslumu, esant tam tikram pagrindui b (paprastai b = 10). Pavyzdžiui, pirmojoje Brigso lentelėje buvo pateikti visų sveikųjų skaičių iš intervalo 1-1000 bendrieji logaritmai 8 skaitmenų tikslumu. Kadangi funkcija f(x) = b ^xyra atvirkštinė log _b(x) funkcija, ji vadinama antilogaritmu. Šias lenteles žmonės naudojo skaičiams dauginti ir dalyti. Pavyzdžiui, naudotojas lentelėje ieškodavo kiekvieno iš dviejų teigiamų skaičių logaritmo. Sudėjus skaičius iš lentelės, gaudavo sandaugos logaritmą. Tada lentelės antilogaritmo funkcija rastų sandaugą pagal jos logaritmą.

Atliekant rankinius skaičiavimus, kuriems reikia tikslumo, atlikti dviejų logaritmų paiešką, apskaičiuoti jų sumą arba skirtumą ir rasti antilogaritmą yra daug greičiau nei dauginti ankstesniais būdais.

Daugelyje logaritmų lentelių logaritmai pateikiami atskirai nurodant x charakteristiką ir mantisą, t. y. log₁₀ (x) sveikąją dalį ir trupmeninę dalį. 10 - x charakteristika yra vienas plius x charakteristika, o jų reikšmės yra vienodos. Tai išplečia logaritmų lentelių taikymo sritį: turint lentelę, kurioje išvardyti log ₁₀(x) visiems sveikiesiems skaičiams x nuo 1 iki 1000, logaritmas 3542 aproksimuojamas taip

log 10 ( 3542 ) = log 10 ( 10 ⋅ 354,2 ) = 1 + log 10 ( 354,2 ) ≈ 1 + log 10 ( 354 ) . {\displaystyle \log _{10}(3542)=\log _{10}(10\cdot 354.2)=1+\log _{10}(354.2)\aprox 1+\log _{10}(354).\,} $\log _{10}(3542)=\log _{10}(10\cdot 354.2)=1+\log _{10}(354.2)\approx 1+\log _{10}(354).\,$

Dar vienas labai svarbus prietaisas buvo slankmatis - logaritmiškai padalytų skalių pora, naudojama skaičiavimams, kaip parodyta šiame paveikslėlyje:

Skaičiai žymimi slankiosiose skalėse atstumais, proporcingais jų logaritmų skirtumams. Atitinkamas viršutinės skalės slinkimas prilygsta mechaniniam logaritmų sudėjimui. Pavyzdžiui, sudėjus atstumą nuo 1 iki 2 apatinėje skalėje su atstumu nuo 1 iki 3 viršutinėje skalėje, gaunama sandauga 6, kuri nuskaitoma apatinėje dalyje. Daugelis inžinierių ir mokslininkų iki XX a. septintojo dešimtmečio naudojo slankmačius. Mokslininkai, naudodamiesi slankmačiu, gali dirbti greičiau nei naudodamiesi logaritmų lentele.

Schematiškai pavaizduota slankmačio taisyklė. Pradėdami nuo 2 apatinėje skalėje, pridėkite atstumą iki 3 viršutinėje skalėje ir gaukite sandaugą 6. Slankioji taisyklė veikia, nes ji pažymėta taip, kad atstumas nuo 1 iki x yra proporcingas x logaritmui.

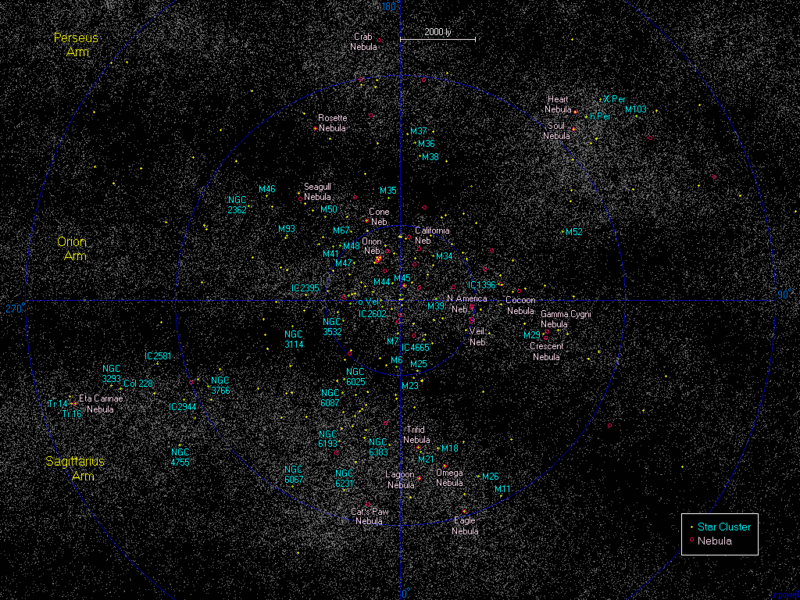
Artimiausios miglų ir žvaigždžių spiečiai (spustelėjamas žemėlapis)

Klausimai ir atsakymai

K: Kas yra logaritmai?

A: Logaritmai yra matematikos dalis, susijusi su eksponentinėmis funkcijomis. Jie nurodo, kokio eksponento reikia tam tikram skaičiui sudaryti, ir yra atvirkštiniai eksponentiškumui.

K: Kaip logaritmai buvo naudojami istoriškai?

A: Logaritmai istoriškai buvo naudingi dauginant arba dalijant didelius skaičius.

K: Koks yra logaritmo pavyzdys?

A: Logaritmo pavyzdys yra log₂(8)=3, kur pagrindas yra 2, argumentas - 8, o atsakymas - 3.

K: Ką reiškia šis pavyzdys?

A: Šis pavyzdys reiškia, kad du, pakelti iki trijų galybės (2³), yra lygūs aštuoniems (2x2x2=8).

K: Kokie yra kai kurie įprasti logaritmų tipai?

Atsakymas: Kai kurie įprasti logaritmų tipai yra 10 pagrindo paprastieji logaritmai, 2 pagrindo dvejetainiai logaritmai ir natūriniai logaritmai, kurių pagrindas e ≈ 2,71828.