AlegsaOnline.com

Slankioji liniuotė (logaritminė liniuotė) – mechaninis analoginis kompiuteris

Atraskite slankiąją liniuotę — mechaninį analoginį kompiuterį: istorija, veikimas, skalės ir praktinis panaudojimas aviacijoje, inžinerijoje bei kasdieniuose skaičiavimuose.

Autorius: Leandro Alegsa

10-12-2025

Slankioji liniuotė, dar vadinama slipstick arba logaritmine liniute, yra mechaninis analoginis kompiuteris, sukurtas spartinti skaičiavimus be elektronikos pagalbos. Ji daugiausia naudojama daugybai ir dalybai, taip pat „mokslinėms“ funkcijoms, tokioms kaip šaknys, logaritmai ir trigonometrija, tačiau paprastai nenaudojama sudėčiai ir atimčiai. Slankioji liniuotė yra patikimas ir greitas įrankis atliekant daugkartinius, daugeliui skaičių reikalingus skaičiavimus ir suteikia praktišką supratimą apie logaritminius santykius.

Sandara ir pagrindiniai elementai

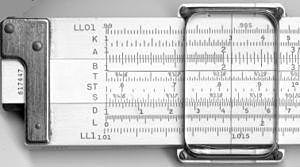
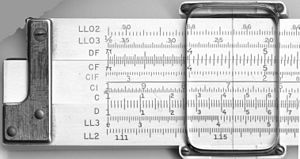
Tipinė slankioji liniuotė susideda iš trijų pagrindinių dalių: fiksuotos pagrindo dalies (statinio arba „statoriaus“), slankiklio (stumdomos plokštelės) ir žymeklio (plonyčio stikliniu ar metalo siūleliu pažymėto indikatorius). Ant jų išgraviruotos standartizuotos žymos (vadinamos skalėmis), kurios atitinka įvairias matematines funkcijas. Dažniausiai pasitaikančios skalės yra D ir C (pagrindinės daugybos/dalijimos skalės), A ir B (kvadratams ir kvadratinėms šaknims), S, T ir ST (trigonometrijai), taip pat LL skalės eksponentams ir logaritmams.

Kaip tai veikia

Slankioji liniuotė veikia naudodama idėją, kad atstumas nuo nulio iki tam tikros reikšmės skalėje proporcingas tos reikšmės logaritmui. Šią idėją pirmasis praktiškai pritaikė Džonas Napjeras, o į pirmuosius slankiojos liniuotės modelius reikšmingai prisidėjo XVI a. Viljamas Oughtredas. Pagrindinė operacija – daugyba – atliekama atitinkamai sudedant logaritmus: ant vienos skalės sukeliamas vienas veiksnys, o ant kitos – kitas, tada atitinkamu stumdu laikydamiesi žymeklio gaunate rezultatą.

Paprastas daugybos pavyzdys: norint padauginti 2 × 3, nustatykite slankiklį taip, kad 1 ant C skalės būtų virš 2 ant D skalės; tada 3 ant C skalės žemiau atitiks rezultatą 6 ant D skalės. Dalyba atliekama atvirkštine tvarka. Tam tikros skalės ir žymeklio plonumas leidžia pasiekti didelį greitį, nors su apribotu tikslumu.

Tipai ir specialios paskirties liniuotės

Yra daug slankiojų liniuočių tipų:

linijinės (tiesinės) — dažniausiai paplitusi forma, patogi rankiniam naudojimui;
apskritiminės — turi skales išdėstytas apskritime ir leidžia sutalpinti ilgesnes skalės atkarpas mažesniame plote;
cilindrinės (pvz., Fuller tipo) — skalė suvyniota ant cilindro, suteikianti labai didelę skalių ilgį ir aukštą tikslumą;
specializuotos – skirtos aviacijoje, finansų srityje ar kitoms sritims, turinčios papildomas skales konkretiems skaičiavimams.

Istorija ir plėtra

Slankioji liniuotė remiasi Džono Napjero logaritmų idėjomis. XVI–XVII a. idėją mechaniniu pavidalu tobulino Viljamas Oughtredas ir kiti matematikai bei konstruktorai. Prieš elektroninių skaičiuotuvų išplitimą slankioji liniuotė buvo pagrindinis technikų, mokslininkų ir inžinierių darbo įrankis – plačiai naudota mokslo ir inžinerijos srityse.

XX a. viduryje, ypač skaitmeninių skaičiavimo prietaisų atsiradimo metu, slankmačių populiarumas trumpam dar augo technologijų ir pramonės poreikiams. Tačiau nuo 1970-ųjų pradžios, o ypač apie 1974 m., dėl prieinamų ir nebrangių kišeninių skaičiuotuvų slankioji liniuotė palaipsniui ėmė nykti kaip kasdienis darbo įrankis ir daug gamintojų pasitraukė iš rinkos.

Tikslumas, ribotumai ir skaitymas

Tikslumas paprastai ribojamas skalės ilgio ir žmogaus gebėjimo tiksliai sustatyti žymeklį; daugumai komercinių slankmačių pasiekiamas tikslumas yra apie 3 reikšmingus skaičius (kartais 4). Viena iš svarbių savybių — dešimtainio kablelio vieta nėra pažymėta skalėje, todėl vartotojas turi nustatyti dešimtainį mastelį pagal kontekstą ar apytikslį dydį.

Ribotumai:

nepatogios ar neįmanomos tiesioginės sudėties ir atimties operacijos;
ribotas skaičių reikšmių intervalas ant vienos skalės ir susijęs tikslumo apribojimas;
reikalingas vartotojo įgūdis ir supratimas, kaip interpretuoti rezultatus ir dešimtainį kablelį.

Priežiūra ir medžiagos

Slankiojimas turi būti laisvas, bet ne per laisvas. Tradiciškai liniuotės gamintos iš medžio (pvz., bambuko), dažnai padengto celuloidine plėvele, arba iš metalo (aliuminio). Reikėtų vengti riebalų ir tirpiklių — valyti sausa arba šiek tiek drėgna šluoste; jei reikalinga, galima naudoti labai mažai specialaus silikoninio tepalo slankiklio vidinėms dalims, bet geriausia laikyti liniuotę sausoje vietoje ir vengti ekstremalių temperatūrų, kad nesideformuotų medinės dalys.

Gamyba, modeliai ir kolekcionavimas

Per kelis šimtmečius susiformavo daugybė modelių ir gamintojų (pvz., stoiškos linijos, Mannheim stiliaus modeliai, profesionalios inžinerinės liniuotės). Nors komercinė paklausa sumažėjo, slankiosios liniuotės išlieka kolekcionavimo objektu, o kai kurie entuziastai ir muziejai saugo istoriškai vertingus egzempliorius. Taip pat egzistuoja atgaivinimo judėjimai, kai liniuotės naudojamos mokymuose, siekiant iliustruoti logaritmų prasmę ir gerinti skaičiavimo intuiciją.

Šiuolaikinė reikšmė

Nors dabar daug kas atlieka skaičiavimus elektroniniais prietaisais, slankioji liniuotė išlieka svarbi kaip istorinis ir mokomasis įrankis. Ji padeda suprasti logaritmų ir santykių sąvokas, moko darbo su masteliais ir apytiksliu skaičiavimu. Kolekcionieriai vertina retus ir aukštos kokybės modeliust, o specializuoti modeliai vis dar naudojami tam tikrose srityse, kur reikia greito apytikslio rezultato be energijos šaltinio.

Tipiška dešimties colių studentų slankmačio taisyklė (Pickett N902-T simplex trig)

Lygiagretė, padėta taip, kad būtų dauginama iš 2. Kiekvienas skaičius D (apatinėje) skalėje yra dvigubas skaičiui, esančiam virš jo C (vidurinėje) skalėje.

Pagrindinės sąvokos

Pačios paprasčiausios formos slankmačiai naudoja dvi logaritmines skales, kad būtų galima greitai dauginti ir dalyti skaičius. Atliekant šiuos įprastus veiksmus popieriuje, gali prireikti daug laiko ir klaidų. Sudėtingesnės slankmačio taisyklės leidžia atlikti kitus skaičiavimus, pavyzdžiui, kvadratinių šaknų, eksponentų, logaritmų ir trigonometrinių funkcijų skaičiavimus.

Matematiniai skaičiavimai atliekami slankiojančioje centrinėje juostelėje esantį ženklą sulygiuojant su ženklu vienoje iš fiksuotų juostelių. Tuomet galima stebėti santykinę kitų ženklų padėtį. Su ženklais sulygiuoti skaičiai parodo apytikslę sandaugos, koeficiento ar kito apskaičiuoto rezultato vertę.

Naudotojas, remdamasis protiniu vertinimu, nustato dešimtainio taško vietą rezultate. Atliekant oficialesnius skaičiavimus, dešimtainio taško vieta nustatoma moksliniu užrašu. Skaičiavimo sudėties ir atimties veiksmai paprastai atliekami mintyse arba popieriuje, o ne slankmačiu.

Dauguma slankmačių turi tris vienodo ilgio linijines juostas. Juostelės yra lygiagrečios ir tarpusavyje sujungtos taip, kad centrinę juostelę būtų galima judinti išilgai kitų dviejų juostų atžvilgiu. Dvi išorinės juostelės yra fiksuotos, todėl jų santykinė padėtis nesikeičia.

Kai kurių slankmačių (dvipusių modelių) skalės yra abiejose skalės ir slankmačio juostelės pusėse, kitų - vienoje išorinių juostelių pusėje ir abiejose slankmačio juostelės pusėse, dar kitų - tik vienoje pusėje (simpleksinės taisyklės). Slankiojančiuoju žymekliu su vertikalia išlyginimo linija galima rasti atitinkamus taškus ant skalių, kurios nėra viena šalia kitos arba, jei tai dvipusiai modeliai, yra kitoje taisyklės pusėje. Žymekliu taip pat galima įrašyti tarpinį rezultatą bet kurioje iš skalių.

Skaičiavimams naudojant slankmatį

Daugyba

Logaritmas daugybos ir dalybos veiksmus paverčia sudėties ir atimties veiksmais pagal taisykles log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} $\log(xy)=\log(x)+\log(y)$ ir log ( x / y ) = log ( x ) - log ( y ) {\displaystyle \log(x/y)=\log(x)-\log(y)} $\log(x/y)=\log(x)-\log(y)$ . Perkėlus viršutinę skalę į dešinę log ( x ) {\displaystyle \log(x)} atstumu. $\log(x)$ Sulyginus viršutinės skalės pradžią su apačioje esančia etikete x {\displaystyle x}, kiekvienas skaičius y {\displaystyle y} sulygiuojamas su kiekvienu skaičiumi y {\displaystyle y}. log ( y ) {\displaystyle \log(y)} $\log(y)$ viršutinėje skalėje su skaičiumi, esančiu log ( x ) + log ( y ) {\displaystyle \log(x)+\log(y)} $\log(x)+\log(y)$ apatinėje skalėje. Kadangi log ( x ) + log ( y ) = log ( x y ) {\displaystyle \log(x)+\log(y)=\log(xy)} $\log(x)+\log(y)=\log(xy)$ , ši padėtis apatinėje skalėje duoda x y {\displaystyle xy} $xy$ x {\displaystyle x} ir y {\displaystyle y} sandauga. Pavyzdžiui, norint apskaičiuoti 3*2, 1 viršutinėje skalėje perkeliamas į 2 apatinėje skalėje. Atsakymas, 6, nuskaitomas iš apatinės skalės, kur 3 yra viršutinėje skalėje. Apskritai viršuje esantis 1 perkeliamas į apačioje esantį veiksnį, o atsakymas nuskaitomas iš apačios, kur kitas veiksnys yra viršuje.

A slide rule, aligned to calculate 2×x

Veiksmai gali būti atliekami "ne pagal skalę", pavyzdžiui, pirmiau pateiktoje diagramoje matyti, kad viršutinėje skalėje esantis skaičius 7 nėra aukščiau už bet kurį skaičių apatinėje skalėje, todėl ji neduoda jokio atsakymo į 2×7. Tokiais atvejais naudotojas gali pastumti viršutinę skalę į kairę, kol jos dešinysis indeksas susilygins su skaičiumi 2, ir dauginti ne iš 2, o iš 0,2, kaip parodyta toliau pateiktoje iliustracijoje:

Šiuo atveju slankmačio naudotojas turi nepamiršti tinkamai pakoreguoti dešimtainį tašką, kad ištaisytų galutinį atsakymą. Norėjome rasti 2×7, bet vietoj to apskaičiavome 0,2×7=1,4. Taigi tikrasis atsakymas yra ne 1,4, o 14. Skaičiuoklės iš naujo nustatymas nėra vienintelis būdas spręsti daugybos, dėl kurios gautume ne pagal skalę rezultatus, pavyzdžiui, 2×7; yra ir kitų būdų:

(1) Naudokite dvigubo dešimtmečio A ir B skales.
(2) Naudokite sulankstytas svarstykles. Šiame pavyzdyje kairįjį C 1 nustatykite priešais D 2. CF žymeklį perkelkite į 7 ir rezultatą perskaitykite iš DF.
(3) Naudokite apverstą CI skalę. CI skalėje 7 padėkite virš 2 D skalėje, o tada rezultatą nuskaitykite iš D skalės, žemiau 1 CI skalėje. Kadangi 1 yra dviejose CI skalės vietose, viena iš jų visada bus skalėje.
(4) Naudokite CI apverstą skalę ir C skalę. CI 2 sulygiuokite su D 1 ir rezultatą skaitykite iš D, žemiau C skalės 7.

1 metodą lengva suprasti, tačiau dėl jo prarandamas tikslumas. 3 metodo privalumas yra tas, kad jį taikant naudojamos tik dvi skalės.

Skyrius

Toliau pateiktoje iliustracijoje parodyta, kaip apskaičiuoti 5,5/2. Viršutinėje skalėje esantis skaičius 2 uždėtas ant apatinėje skalėje esančio skaičiaus 5,5. Viršutinėje skalėje esantis 1 yra virš kvanto 2,75. Yra daugiau nei vienas dalijimo būdas, tačiau čia pateiktas būdas turi pranašumą, nes galutinis rezultatas negali būti ne pagal skalę, nes galima pasirinkti, ar naudoti 1 abiejuose galuose.

A slide rule, aligned to calculate x÷5.5

Kitos operacijos

Be logaritminės skalės, kai kuriose slankmačiuose yra ir kitų matematinių funkcijų, užkoduotų kitose pagalbinėse skalėse. Populiariausios buvo trigonometrinės, paprastai sinuso ir tangento, bendrojo logaritmo (log10) (reikšmės logaritmui daugiklio skalėje priimti), natūraliojo logaritmo (ln) ir eksponentinės (e^x ) skalės. Kai kurios taisyklės apima Pitagoro skalę, skirtą trikampių kraštinėms apskaičiuoti, ir skalę apskritimams apskaičiuoti. Kitose taisyklėse yra skalės hiperbolinėms funkcijoms skaičiuoti. Linijinėse taisyklėse skalės ir jų žymėjimas yra labai standartizuoti, paprastai skiriasi tik tai, kurios skalės yra įtrauktos ir kokia tvarka:

A, B	dviejų dekadų logaritminės skalės, naudojamos skaičių kvadratinėms šaknims ir kvadratams rasti.
C, D	vieno dešimtmečio logaritminės skalės
K	trijų dekadų logaritminė skalė, naudojama kubo šaknims ir skaičių kubams rasti
CF, DF	"sulankstytos" C ir D skalių versijos, kurios prasideda nuo π, o ne nuo vieneto; tai patogu dviem atvejais. Pirma, kai naudotojas spėja, kad produktas bus artimas 10, bet nėra tikras, ar jis bus šiek tiek mažesnis, ar šiek tiek didesnis už 10, sulankstytos skalės leidžia išvengti galimybės nukrypti nuo skalės. Antra, kadangi pradžia yra π, o ne kvadratinė šaknis iš 10, supaprastėja dauginimas arba dalijimas iš π (kaip įprasta mokslo ir inžinerijos formulėse).
CI, DI, DIF	"apverstos" skalės, einančios iš dešinės į kairę, naudojamos 1/x žingsniams supaprastinti.
S	naudojamas sinusams ir kosinusams D skalėje rasti
T	naudojamas tangentams ir katangentams D ir DI skalėse rasti
ST, SRT	naudojamas mažų kampų sinusams ir tangentams bei laipsnių ir radianų konvertavimui
L	linijinė skalė, naudojama kartu su C ir D skalėmis 10 bazės logaritmams ir 10 galybėms rasti.
LLn	logaritminės-logaritminės skalės, naudojamos skaičių logaritmams ir eksponentams rasti.
Ln	tiesinė skalė, naudojama kartu su C ir D skalėmis natūraliesiems (e pagrindo) logaritmams ir e x {\displaystyle e^{x}} rasti. $e^{x}$

A slide rule designed to calculate 2 x X

A slide rule designed to calculate 0.2 x X

K&E 4081-3 slankmačio skalės priekyje ir gale.

1931 m. "Gilson" pagaminta dvejetainė slankmačio taisyklė atliko tik trupmenų sudėties ir atimties funkciją.

Šaknys ir galios

Skiriamos vienos dekados (C ir D), dviejų dekadų (A ir B) ir trijų dekadų (K) skalės. Norint apskaičiuoti x 2 {\displaystyle x^{2}} $x^{2}$ pavyzdžiui, raskite x D skalėje ir nuskaitykite jo kvadratą A skalėje. Apvertus šį procesą, galima rasti kvadratines šaknis, panašiai galima rasti 3, 1/3, 2/3 ir 3/2 galybes. Reikia būti atsargiems, kai pagrindas x randamas daugiau nei vienoje skalės vietoje. Pavyzdžiui, A skalėje yra du devynetai; norėdami rasti kvadratinę šaknį iš devynių, pasinaudokite pirmuoju; antrasis duoda kvadratinę šaknį iš 90.

Spręsdami x y {\displaystyle x^{y}} $x^{y}$ uždavinius, naudokite LL skales. Kai yra kelios LL skalės, naudokite tą, kurioje yra x. Pirmiausia sulygiuokite kraštinį kairįjį 1 C skalėje su x LL skalėje. Tada suraskite y C skalėje ir pereikite prie LL skalės, kurioje yra x. Ši skalė nurodys atsakymą. Jei y yra "ne pagal skalę", raskite x y / 2 {\displaystyle x^{y/2}} $x^{y/2}$ ir išlyginkite jį naudodami A ir B skales, kaip aprašyta pirmiau.

Trigonometrija

S, T ir ST skalės naudojamos trigonometrinėms funkcijoms ir trigonometrinių funkcijų daugikliams, kampams laipsniais. Daugelio slankmačių S, T ir ST skalės pažymėtos laipsniais ir minutėmis. Vadinamuosiuose decitriginiuose modeliuose vietoj laipsnių naudojamos dešimtainės laipsnių trupmenos.

Logaritmai ir eksponentai

Baziniai 10 logaritmai ir eksponentai randami naudojant L skalę, kuri yra tiesinė. Kai kurios slankmačiai turi Ln skalę, kuri skirta e pagrindui.

Ln skalę 1958 m. išrado 11 klasės mokinys Stephenas B. Cohenas. Iš pradžių buvo siekiama, kad naudotojas Ln skalėje galėtų pasirinkti eksponentą x (nuo 0 iki 2,3) ir C (arba D) skalėje perskaityti e^x, o CI (arba DI) skalėje - e.^–x Pickett, Inc. buvo suteiktos išskirtinės skalės teisės. Vėliau išradėjas sukūrė Ln skalės "ženklų" rinkinį, kad būtų galima išplėsti diapazoną už 2,3 ribos, tačiau "Pickett" šių ženklų niekada neįdiegė į jokias savo slankmačio taisykles. ^[]

Sudėtis ir atimtis

Sklandymo taisyklės paprastai nenaudojamos sudėčiai ir atimčiai, tačiau vis dėlto tai galima padaryti naudojant du skirtingus metodus.

Norint atlikti sudėties ir atimties veiksmus C ir D (arba bet kurioje kitoje panašioje skalėje), pirmiausia reikia pakeisti uždavinį į dalybos uždavinį. Sudedant du kintamuosius ir daliklį padauginus iš dviejų kintamųjų ir padauginus iš vieno, jų suma lygi jų sumai:

x + y = ( x y + 1 ) y {\displaystyle x+y=\left({\frac {x}{y}}+1\right)y} $x+y=\left({\frac {x}{y}}+1\right)y$

Atimant dviejų kintamųjų santykis, iš dviejų kintamųjų atėmus daliklį ir padauginus jį iš vieno, yra lygus jų skirtumui:

x - y = ( x y - 1 ) y {\displaystyle x-y=\left({\frac {x}{y}}-1\right)y} $x-y=\left({\frac {x}{y}}-1\right)y$

Šis metodas panašus į sudėties ir atimties metodą, naudojamą didelės spartos elektroninėse grandinėse su logaritmine skaičių sistema specializuotose kompiuterių programose, pavyzdžiui, superkompiuteryje "Gravity Pipe" (GRAPE) ir paslėptuose Markovo modeliuose.

Antruoju metodu naudojama slankioji linijinė L skalė, kurią galima naudoti kai kuriuose modeliuose. Sudėtis ir atimtis atliekama stumdant žymeklį į kairę (atimčiai) arba į dešinę (sudėčiai) ir grąžinant slankiklį į 0, kad būtų perskaitytas rezultatas.

Fizinis dizainas

Standartinės linijinės taisyklės

Slankmačio ilgis nurodomas kaip nominalus skalių ilgis. Dažniausiai naudojamų "10 colių" modelių skalės iš tikrųjų yra 25 cm ilgio, nes jos buvo pagamintos pagal metrinius standartus, nors kai kuriose taisyklėse skalės yra šiek tiek ilgesnės, kad būtų paprasčiau manipuliuoti, kai rezultatas perpildytas. Kišeninės taisyklės paprastai yra 5 colių. Buvo parduodami poros metrų ilgio modeliai, kurie buvo kabinami klasėse mokymo tikslais. [1]

Paprastai padalomis skalė žymima dviejų reikšminių skaičių tikslumu, o naudotojas įvertina trečiąjį skaičių. Kai kurios aukštos klasės slankmačiai turi didinamuosius žymeklius, kad žymes būtų lengviau įžiūrėti. Tokie žymekliai gali padvigubinti rodmenų tikslumą, todėl 10 colių slankmatis gali tarnauti taip pat gerai kaip 20 colių.

Sukurta įvairių kitų patogumų. Trigonometrinės skalės kartais žymimos dviem ženklais - juodai ir raudonai, nurodant vienas kitą papildančius kampus (vadinamasis "Darmštato" stilius). Dvigubos slankmačių taisyklės dažnai dubliuoja kai kurias skales kitoje pusėje. Siekiant didesnio tikslumo, skalės dažnai "dalijamos".

Įvairioms inžinerijos, verslo ir bankininkystės sritims buvo išrastos specializuotos slankmačių taisyklės. Dažnai jose bendri skaičiavimai buvo tiesiogiai išreikšti specialiomis skalėmis, pavyzdžiui, paskolų skaičiavimai, optimalūs pirkimo kiekiai arba tam tikros inžinerinės lygtys. Pavyzdžiui, bendrovė "Fisher Controls" platino specialiai pritaikytą slankmatį, pritaikytą lygtims, naudojamoms tinkamam pramoninių srauto reguliavimo vožtuvų dydžiui parinkti, spręsti. ^[]

Apskritosios slankmačių taisyklės

Skritulinės slankmačio taisyklės būna dviejų pagrindinių tipų: vienos su dviem žymekliais (kairėje), kitos su judančiu disku ir vienu žymekliu (dešinėje). Dviejų žymeklių versijos daugybą ir dalybą atlieka išlaikydamos fiksuotą kampą tarp žymeklių, kai jie sukami aplink diską. Vieno kursoriaus versija veikia panašiau į standartinę slankmačio skalę, nes skalės yra tinkamai suderintos.

Pagrindinis apskritimo slankmačio privalumas yra tas, kad ilgiausias įrankio matmuo sumažintas maždaug 3 kartus (t. y. π). Pavyzdžiui, 10 cm ilgio apskritiminio slankmačio išorinės skalės didžiausias tikslumas būtų lygus 30 cm ilgio įprasto slankmačio tikslumui. Apskritosios slankmačio taisyklės taip pat leidžia išvengti skaičiavimų "ne pagal skalę", nes skalės buvo sukurtos taip, kad jas būtų galima "apvynioti"; jų niekada nereikia perorientuoti, kai rezultatai yra artimi 1,0 - taisyklė visada atitinka skalę. Tačiau naudojant neciklines nespiralines skales, pavyzdžiui, S, T ir LL, skalės ilgis sutrumpėja, kad liktų vietos galiniams kraštams.

Apskritosios slankmačiai yra mechaniškai tvirtesni ir sklandžiau juda, tačiau jų skalės sureguliavimo tikslumas priklauso nuo centrinės ašies centravimo; vos 0,1 mm nukrypimas nuo ašies centro gali lemti 0,2 mm blogiausiu atveju sureguliavimo paklaidą. Tačiau šarnyras neleidžia subraižyti ciferblato ir žymeklių. Didžiausio tikslumo skalės yra ant išorinių žiedų. Aukštos klasės apskritiminėse taisyklėse sudėtingesnėms operacijoms, pavyzdžiui, logaritminėms skalėms, vietoj "padalintų" skalių naudojamos spiralinės skalės. Vienoje aštuonių colių aukščiausios klasės apvaliojoje taisyklėje buvo 50 colių spiralinė logaritminė skalė.

Pagrindiniai diskinių slankmačių trūkumai yra šie: sunku nustatyti figūrų padėtį išilgai besisukančio disko ir ribotas skalių skaičius. Dar vienas apskritiminių slankmačių trūkumas yra tas, kad mažiau svarbios skalės yra arčiau centro ir jų tikslumas yra mažesnis. Dauguma mokinių išmoko naudotis linijinėmis slankmačio taisyklėmis ir nerado priežasčių jas keisti.

Viena iš pasaulyje kasdien naudojamų slankmačių yra E6B. Tai apskrita slankmačio taisyklė, pirmą kartą sukurta 1930 m. lėktuvų pilotams, kad padėtų skaičiuoti mirus. Ant rėmo atspausdintos skalės taip pat padeda atlikti įvairias užduotis, pavyzdžiui, perskaičiuoti laiko, atstumo, greičio ir temperatūros vertes, kompaso paklaidas ir apskaičiuoti sunaudojamų degalų kiekį. Vadinamąjį "maldos ratą" vis dar galima įsigyti skrydžių parduotuvėse ir jis vis dar plačiai naudojamas. Nors GPS sumažino "dead reckoning" naudojimą oro navigacijai, o daugelį jo funkcijų perėmė rankiniai skaičiuotuvai, E6B tebėra plačiai naudojamas kaip pagrindinis arba atsarginis prietaisas, o dauguma skraidymo mokyklų reikalauja, kad jų studentai būtų įgiję tam tikrą jo naudojimo lygį.

1952 m. Šveicarijos laikrodžių bendrovė "Breitling" pristatė piloto rankinį laikrodį su integruota apskrita slankmačio taisykle, skirtą skrydžio skaičiavimams: "Breitling Navitimer". "Navitimer" apvalioji taisyklė, kurią "Breitling" vadino "navigacijos kompiuteriu", turėjo skrydžio greičio, pakilimo ir nusileidimo greičio, skrydžio laiko, atstumo ir degalų sąnaudų funkcijas, taip pat kilometrų ir jūrmylių bei galonų ir litrų degalų kiekio perskaičiavimo funkcijas.

Medžiagos

Tradiciškai slankmačiai buvo gaminami iš kietos medienos, pavyzdžiui, raudonmedžio ar buksmedžio, su stiklo ir metalo kirtikliais. Bent vienas didelio tikslumo instrumentas buvo pagamintas iš plieno.

1895 m. Japonijos įmonė "Hemmi" pradėjo gaminti slankmačius iš bambuko, kuris pasižymėjo matmenų stabilumu, tvirtumu ir savaiminiu tepimu. Šios bambukinės slankmačio taisyklės buvo pristatytos Švedijoje 1933 m. rugsėjį [2], o Vokietijoje tikriausiai tik šiek tiek anksčiau. Skalės buvo gaminamos iš celiuloido arba plastiko. Vėliau slankmačiai buvo gaminami iš plastiko arba aliuminio, nudažyto plastiku. Vėlesni kursoriai buvo akrilo arba polikarbonato, slystantys ant teflono guolių.

Ant visų aukščiausios kokybės slankmačių buvo išgraviruoti skaičiai ir skalės, o paskui užpildyti dažais ar kita derva. Dažytos ar įspaustos slankmačių taisyklės buvo laikomos prastesnėmis, nes ženklai galėjo nusitrinti. Nepaisant to, "Pickett", tikriausiai sėkmingiausia Amerikos skaidrių taisyklų bendrovė, gamino visas atspausdintas skales. Aukščiausios kokybės slankmačiai turėjo įmantrius fiksatorius, kad taisyklė netyčia nesusidėvėtų, ir buferius, apsaugančius skales ir kursorių nuo trinties į stalviršį. Rekomenduojamas graviruotų ženklų valymo būdas - lengvai nušveisti plienine vata. Dažytoms slankmačio taisyklėms ir silpnų nervų žmonėms naudokite atskiestą komercinį langų valymo skystį ir minkštą šluostę.

Piketo apskrita slankmatis su dviem rodyklėmis. (4,25 col. / 10,9 cm skersmens) Reverso pusėje yra papildoma skalė ir vienas žymeklis.

Paprasta apskrita slankmačio skalė, pagaminta Concise Co., Ltd., Tokijas, Japonija, turinti tik atvirkštinę, kvadratinę ir kubinę skales. Kitoje pusėje yra patogus 38 metrinių ir imperinių perskaičiavimo koeficientų sąrašas.

"Breitling Navitimer" rankinis laikrodis su apskrita slankmačio taisykle

Istorija

Lygtis buvo išrasta apie 1620-1630 m., netrukus po to, kai Džonas Napjeras paskelbė logaritmo sąvoką. Edmundas Gunteris iš Oksfordo sukūrė skaičiavimo prietaisą su viena logaritmine skale, kurį, pasitelkus papildomus matavimo įrankius, buvo galima naudoti dauginti ir dalyti. Pirmąjį šios skalės aprašymą 1624 m. Paryžiuje išspausdino anglų matematikas Edmundas Vingatas (Edmund Wingate, apie 1593-1656) knygoje "L'usage de la reigle de proportion en l'arithmetique & geometrie". Knygoje pateikta dviguba skalė, kurios vienoje pusėje yra logaritminė skalė, o kitoje - lentelių skalė. 1630 m. Viljamas Oughtredas iš Kembridžo išrado apskritą slankmačio taisyklę, o 1632 m. jis sujungė dvi Gunterio taisykles, laikytas kartu rankomis, ir sukūrė prietaisą, kuris yra atpažįstamas kaip šiuolaikinė slankmatis. Kaip ir jo amžininkas Kembridže Izaokas Niutonas, Oughtredas privačiai dėstė savo idėjas studentams, bet delsė jas paskelbti, ir, kaip ir Niutonas, įsitraukė į įnirtingą ginčą dėl pirmumo su savo vienmečiu mokiniu Ričardu Delamainu ir ankstesnėmis Wingate'o pretenzijomis. Oughtredo idėjos buvo paviešintos tik jo mokinio Viljamo Forsterio 1632 ir 1653 m. publikacijose.

1677 m. Henris Coggeshalas sukūrė dviejų pėdų sulankstomą taisyklę medienai matuoti, vadinamą Coggeshalo slankmačiu. Dėl jo sukurto įrankio konstrukcijos ir panaudojimo slankmačio taisyklė tapo ne tik matematinio tyrimo priemone.

1722 m. Warneris įvedė dviejų ir trijų dekadų skales, o 1755 m. Everardas įtraukė apverstą skalę; slankmatis su visomis šiomis skalėmis paprastai vadinamas "daugiafaziu" slankmačiu.

1815 m. Peteris Rogetas išrado logaritmo logaritmo slankmatį, kuriame buvo logaritmo logaritmo logaritmą rodanti skalė. Tai leido naudotojui tiesiogiai atlikti skaičiavimus, susijusius su šaknimis ir eksponentais. Tai buvo ypač naudinga trupmeninėms galioms skaičiuoti.

Šiuolaikinė forma

Modernesnę formą 1859 m. sukūrė prancūzų artilerijos leitenantas Amédée Mannheimas, "kuriam pasisekė, kad jo taisyklę pagamino nacionalinės reputacijos įmonė ir kad ją priėmė Prancūzijos artilerija". Maždaug tuo metu, kai inžinerija tapo pripažinta profesine veikla, Europoje plačiai pradėtos naudoti slankmačio taisyklės. Jungtinėse Valstijose jos paplito tik 1881 m., kai Edvinas Tačeris (Edwin Thacher) pristatė cilindrinę taisyklę. Dvipusę taisyklę 1891 m. išrado Viljamas Koksas (William Cox), ją gamino Niujorko bendrovė "Keuffel and Esser Co.".

Astronominiams darbams taip pat reikėjo tikslių skaičiavimų, todėl XIX a. Vokietijoje vienoje observatorijoje buvo naudojama maždaug 2 metrų ilgio plieninė slankmačio taisyklė. Prie jos buvo pritvirtintas mikroskopas, todėl ji buvo tiksli šešių skaičių po kablelio tikslumu.

Antrojo pasaulinio karo metais bombonešiai ir navigatoriai, kuriems reikėjo greitai atlikti skaičiavimus, dažnai naudojo specialias slankmačio taisykles. Vienas JAV karinio jūrų laivyno biuras iš tikrųjų suprojektavo bendrą skaidrių taisyklių "važiuoklę" su aliumininiu korpusu ir plastikiniu valdikliu, į kurį buvo galima įdėti celiulioidines korteles (atspausdintas iš abiejų pusių) specialiems skaičiavimams atlikti. Šis procesas buvo išrastas lėktuvų nuotoliui, degalų sąnaudoms ir aukščiui apskaičiuoti, o vėliau pritaikytas daugeliui kitų tikslų.

Šeštajame ir septintajame dešimtmetyje slankmatis buvo inžinieriaus profesijos simbolis (panašiai kaip stetoskopas simbolizuoja mediko profesiją).^[] Vokiečių raketų mokslininkas Wernheris von Braunas, po Antrojo pasaulinio karo persikėlęs į JAV dirbti su Amerikos kosmoso programa, atsivežė dvi 1930 m. senovines Nestlerio slankmačio taisykles. Visą gyvenimą jis niekada nenaudojo jokių kitų kišeninių skaičiavimo prietaisų; slankmačiai jam puikiai pasitarnavo greitai apskaičiuojant raketų konstrukcijos parametrus ir kitus skaičius. Kaip teigiama ant Pickett's N600 skaidrių taisyklių dėžučių esančioje reklamoje [3], aliumininės Pickett's N600 skaidrių taisyklių dėžutės buvo gabenamos penkiose "Apollo" kosminėse misijose, taip pat ir į Mėnulį.

Kai kurie inžinerijos studentai ir inžinieriai nešiojosi dešimties colių slankmačio taisykles diržo dėkluose, ir net iki aštuntojo dešimtmečio vidurio tai buvo įprastas vaizdas universitetų miesteliuose. Studentai taip pat galėjo turėti dešimties ar dvidešimties colių slankmatį, skirtą tiksliam darbui namuose ar biure, o su savimi nešiotis kišeninį penkių colių slankmatį.

2004 m. švietimo tyrėjai Davidas B. Sheris ir Deanas C. Nataro sugalvojo naujo tipo slankmačio taisyklę, pagrįstą prosthafaerezės principu - greito produktų skaičiavimo algoritmu, kuris buvo sukurtas anksčiau nei logaritmai. Tačiau praktinio susidomėjimo konstruoti tokią skaičiavimo taisyklę, išskyrus pradinį prototipą, buvo nedaug. [4]

Sumažėjimas

Skaičiuoklės svarba ėmė mažėti, kai šeštajame dešimtmetyje elektroniniai kompiuteriai - nauja, bet labai reta priemonė - tapo plačiai prieinami technikos darbuotojams. 1957 m. pradėjus naudoti Fortraną, kompiuteriai tapo praktiški sprendžiant nedidelius matematinius uždavinius. IBM pristatė nebrangesnių kompiuterių seriją: IBM 650 (1954 m.), IBM 1620 (1959 m.), IBM 1130 (1965 m.), skirtą mokslo ir inžinerijos rinkai. Johno Kemeny'o BASIC programavimo kalba (1964 m.) palengvino studentams naudotis kompiuteriais. 1965 m. buvo pristatytas DEC PDP-8 minikompiuteris.

Kompiuteriai taip pat pakeitė skaičiavimo pobūdį. Naudojant slankmačius, daug dėmesio buvo skiriama algebrai, kad išraiškos būtų kuo lengviau apskaičiuojamos. Skaičiavimo taisyklių naudotojai paprasčiausiai aproksimuodavo arba atsisakydavo mažų terminų, kad skaičiavimas būtų paprastesnis. Fortranas leido įvesti sudėtingas formules iš vadovėlių be pastangų jas performuluoti. Skaitmeninis integravimas dažnai būdavo paprastesnis nei bandymas rasti sudėtingų uždavinių uždarosios formos sprendinius. Jaunas inžinierius, prašantis kompiuterio laiko išspręsti uždavinį, kurį buvo galima išspręsti keliais brūkštelėjimais slankmačiu, tapo humoristine kliše. Daugelyje kompiuterių centrų ant sienos kabojo įrėminta skaidrių taisyklė su užrašu "Avarijos atveju išdaužkite stiklą".

Dar vienas žingsnis, siekiant pakeisti slankmačius elektroninėmis priemonėmis, buvo elektroninių skaičiuotuvų, skirtų moksliniam ir inžineriniam naudojimui, kūrimas. Pirmieji iš jų buvo 1965 m. pristatytas "Wang Laboratories LOCI-2", kuriame daugybai ir dalybai buvo naudojami logaritmai, ir 1968 m. pristatytas "Hewlett-Packard HP-9100". Be eksponentų ir logaritmų, HP-9100 turėjo trigonometrines funkcijas (sin, cos, tan). Jame buvo naudojamas CORDIC (koordinačių sukimo skaitmeninis kompiuteris) algoritmas, leidžiantis trigonometrines funkcijas apskaičiuoti naudojant tik poslinkio ir sudėties operacijas. Šis metodas palengvino vis mažesnių mokslinių skaičiuotuvų kūrimą.

Paskutinė vinis į slankmačio karstą buvo pradėti gaminti kišeniniai moksliniai skaičiuotuvai, iš kurių pirmasis 1972 m. buvo "Hewlett-Packard HP-35". Tokie skaičiuotuvai buvo vadinami "skaidrių taisyklių" skaičiuotuvais, nes jie galėjo atlikti daugumą arba visas skaidrių taisyklių funkcijas. Kelių šimtų dolerių kaina daugumai studentų buvo brangi. Nors profesionalios slankmačiai taip pat galėjo būti gana brangūs, vaistinėse dažnai būdavo parduodami pagrindiniai plastikiniai modeliai už mažiau nei 20 JAV dolerių. Tačiau 1975 m. pagrindinius keturių funkcijų elektroninius skaičiuotuvus buvo galima įsigyti už mažiau nei 50 JAV dolerių. 1976 m. TI-30 mokslinį skaičiuotuvą buvo galima įsigyti už mažiau nei 25 JAV dolerius. Po šio laikotarpio skaidrių taisyklių rinka greitai išseko, nes maži moksliniai skaičiuotuvai tapo įperkami.

Viljamas Oughtredas (1575-1660), apskritosios slankmačio skalės išradėjas

Inžinierius naudoja slankmatį. Fone atkreipkite dėmesį į mechaninį skaičiuotuvą.

Privalumai

Sklandymo taisyklė yra linkusi sušvelninti "klaidingo tikslumo" ir reikšmingumo klaidą. Įprastas tikslumas, kuriuo gali naudotis slankmačio taisyklė, yra maždaug trys tikslumo vietos. Tai gerai atitinka daugumą duomenų, kuriuos galima įvesti į inžinerines formules. Naudojant šiuolaikinį kišeninį skaičiuotuvą, tikslumas gali būti rodomas iki septynių ar daugiau ženklų po kablelio, nors iš tikrųjų rezultatai niekada nebus tikslesni už turimus įvesties duomenis.
Naudojant slankmačio taisyklę reikia nuolat vertinti rezultatų eiliškumą. Naudojant slankmačio taisyklę 1,5 × 30 (kuris lygus 45) rodys tą patį rezultatą kaip 1 500 000 × 0,03 (kuris lygus 45 000). Inžinierius turi nuolat nustatinėti rezultatų pagrįstumą, o tai gali būti prarasta, kai skaičiai neatsargiai įvedami į kompiuterio programą arba skaičiuotuvą.
Atliekant daugybos ar dalybos iš to paties skaičiaus seką, atsakymą dažnai galima nustatyti tiesiog žvilgtelėjus į slankmatį ir nieko nedarant. Tai gali būti ypač naudinga skaičiuojant procentus, pvz., testų rezultatus, arba lyginant kainas, pvz., doleriais už kilogramą. Daugybę greičio, laiko ir atstumo skaičiavimų su slankmačiu galima atlikti vos žvilgtelėjus į jį rankomis.
Skaičiuoklė nepriklauso nuo elektros energijos.
Lygiagretainis yra lengvai atkartojama technologija. Iš pateikto slankmačio pavyzdžio kompetentingas amatininkas gali pagaminti daugiau iš elementarių medžiagų, naudodamas nepramoninius procesus.
Skaidrių taisyklės yra labai standartizuotos, todėl pereinant prie kitos taisyklės nereikia nieko iš naujo mokytis.
Stumdomosios taisyklės yra universalios, jomis galima naudotis tokiose situacijose ir aplinkoje, kur naudotojo vikrumas gali būti ribotas (pvz., dėl apsauginių pirštinių reikalingumo). Priešingai, tokiose situacijose gali būti sunku naudotis skaičiuotuvu - mažai tikėtina, kad naudojant slankmačio taisyklę bus padaryta klaida, panaši į tą, kuri atsiranda per klaidą paspaudus ne tą skaičiuotuvo mygtuką.
Sklandymo taisykles galima pasigaminti iš kartono arba popieriaus. Daugelis nemokamų diagramų ar specializuotų skaičiavimo prietaisų, pagamintų iš kartono, iš tikrųjų yra specializuotos linijinės ar apskritiminės slankmačio taisyklės.

Naudojant slankmatį kartu su elektroniniu skaičiuotuvu vienas iš privalumų yra tas, kad svarbų skaičiavimą galima patikrinti abiem prietaisais; kadangi abu prietaisai labai skirtingi, yra maža tikimybė padaryti tą pačią klaidą du kartus.

Trūkumai

Klaidos gali atsirasti dėl mechaninio netikslumo.
Skaičiavimai naudojant slankmatį yra riboto tikslumo dėl jų analoginių įėjimų ir išėjimų. Ir atvirkščiai, dėl diskrečių skaitinių įvesties ir elektroninių operacijų su slankiuoju kableliu net ir kuklių šiuolaikinių skaičiuotuvų išvesties skiriamoji geba yra bent šeši reikšminiai skaičiai.

Susiję puslapiai

Klausimai ir atsakymai

K: Kas yra slankmatis?

A.: Lygiagretė yra mechaninis analoginis kompiuteris, dažniausiai naudojamas daugybai ir dalybai, taip pat mokslinėms funkcijoms, tokioms kaip šaknų, logaritmų ir trigonometrijos, atlikti.

K: Kokios yra skirtingos skaidrių taisyklių rūšys?

A: Skaidulinės taisyklės gali būti linijinės arba apskritos ir turėti standartizuotą ženklų arba skalių rinkinį, naudojamą matematiniams skaičiavimams atlikti. Kai kurios specialios paskirties slankmačiai buvo pagaminti aviacijai ar finansams su specialiomis skalėmis.

Klausimas: Kas išrado slankmačio taisyklę?

A: Slankiąją taisyklę išrado Viljamas Oughtredas (William Oughtred), remdamasis Džono Napjero (John Napier) logaritmų darbu.

K: Kada buvo sukurti elektroniniai skaičiuotuvai?

A.: Elektroniniai skaičiuotuvai buvo sukurti iki 1970 m., tačiau apie 1974 m. kišeninis skaičiuotuvas iš esmės pavertė slankmatį pasenusiu.

K: Ką žmonės dažniausiai naudojo gamtos ir technikos moksluose prieš sukuriant elektroninius skaičiuotuvus?

A.: Prieš sukuriant elektroninius skaičiuotuvus, mokslo ir technikos srityje žmonės dažniausiai naudojo slankmačius.

K: Kiek laiko žmonės naudojo slankmatį po to, kai buvo pradėti naudoti skaitmeniniai skaičiavimo prietaisai?

A.: Žmonės ir toliau naudojo slankmatį šeštajame ir septintajame dešimtmetyje, net ir tada, kai pamažu buvo pradėti naudoti skaitmeniniai skaičiavimo prietaisai.