Daugyba apibrėžimas, savybės ir pavyzdžiai
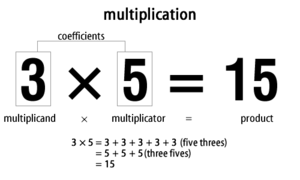
Daugyba – tai aritmetinis veiksmas, kuriuo nustatoma dviejų skaičių sandauga. Daugyba yra vienas iš pagrindinių aritmetikos veiksmų, kartu su sudėtimi, atimtimi ir dalyba.
Apibrėžimas ir interpretacijos
Naudojant natūraliuosius skaičius, daugybą galima suprasti kaip kartotinę sudėtį: a × b reiškia a kartų b arba b kartų a. Geometrinė interpretacija – skaičiuoti plyteles stačiakampyje: vienas skaičius nurodo plytelių skaičių vienoje kraštinėje, kitas – kitoje kraštinėje; bendras plytelių skaičius yra sandauga (stačiakampyje, pavyzdžiui 3 × 5 = 15).
Naudojant realiuosius skaičius, daugyba atitinka ilginių skalavimą ir leidžia apskaičiuoti stačiakampio, kurio pirmasis skaičius yra lygus vienos kraštinės dydžiui, o antrasis – kitos kraštinės dydžiui, plotą. Taip pat daugyba interpretuojama kaip mastelio keitimas: vienas iš dydžių padidintas (ar sumažintas) kitokiu mastu.
Galima pateikti ir aibes bei kardinalumo interpretacijas: apibrėžus daugybą kaip kartotinę sudėtį, gaunama aibių teorinė kardinalių skaičių daugybos prasmė.
Pagrindinės savybės
- Komutatyvumas: a × b = b × a. Tai galioja daugeliui skaičių sistemų, pavyzdžiui sveikuosiems skaičiams, racionaliesiems skaičiams, visiems realiems skaičiams ir kompleksiniams skaičiams.
- Asociatyvumas: (a × b) × c = a × (b × c). Tai leidžia daugybą rašyti be skliaustų, kai dauginama daugiau nei du skaičiai.
- Distributyvumas: a × (b + c) = a×b + a×c. Daugyba paskirstoma per sudėtį.
- Tapatybės elementas: 1 yra neutri daugikliui: 1 × a = a × 1 = a.
- Nulio savybė: 0 × a = a × 0 = 0. Bet koks skaičius, padauginus iš nulio, duoda nulį.
- Atvirkštinis elementas: kiekvienas nulis nevienas realus skaičius a turi daugiklį a^(-1), toks, kad a × a^(-1) = 1. Tai susiję su dalijimu – dalyba yra daugybos atvirkštinė operacija (dalinti iš a reiškia dauginti iš a^(-1)).
Svarbu: komutatyvumas ir kitos aukščiau nurodytos savybės galioja daugeliui skaičių rinkinių, tačiau ne visur. Pavyzdžiui, tai negalioja ketvertainiams (skaičiams, kuriuos galima pavaizduoti kaip žiedą keturmatėje erdvėje), vektoriams ir matricoms, kur daugyba gali būti nekooperuojanti (nekomutatyvi).
Simboliai ir užrašai
Daugybai naudojami ženklai ×, · arba paprasčiausiai skaičių kartotinė išdėstymo forma (pvz., 3·5 arba 3(5)). Taip pat dauginti reiškia kelti laipsniu: a^n yra a padaugintas iš savęs n kartų (kai n yra natūralus). Eilės tvarka sprendžiant išraiškas: daugyba atliekama prieš sudėtį ir atimtį (veiksmų prioritetas).
Pavyzdžiai
3 × 5 = 15. Tai reiškia trijų penketų sumą arba penkių trejetų sumą. Matematikai du skaičius, kuriuos daugina, dažnai vadina daugikliais arba faktorais.
Keletas papildomų pavyzdžių:
- (-2) × 4 = -8 (dauginant skaičių su neigiamu gaunamas neigiamas rezultatas).
- 2 × (3 + 4) = 2×3 + 2×4 = 6 + 8 = 14 (distributyvumas).
- (2/3) × (3/4) = 6/12 = 1/2 (daugyba trupmenų: dauginame skaitiklius ir vardiklius).
- 5 × 0 = 0 (bet koks skaičius, daugintas iš nulio, duoda nulį).
Ryšys su dalyba
Daugybos priešingybė yra dalijimas: dalinti iš nenulinio skaičiaus reiškia dauginti iš jo atvirkštinio. Pvz., 15 ÷ 3 = 5 reiškia 15 × (1/3) = 5.
Santrauka
Daugyba yra universali operacija su daugeliu prasmių: kartotinė sudėtis, geometrinis plotas ar mastelio keitimas. Ji turi keliolika svarbių savybių (komutatyvumas, asociatyvumas, distributyvumas, tapatybės elementas, nulio savybė), kurios leidžia atlikti skaičiavimus ir kurti sudėtingesnes matematikos konstrukcijas. Kontekste, pavyzdžiui dirbant su matricomis ar tam tikromis algebrinėmis struktūromis, šių savybių galiojimas turi būti aiškiai patikrintas.
Daugybos lentelė
Mokytojai, mokydami daugybos, paprastai reikalauja, kad mokiniai įsimintų pirmųjų 9 skaičių lentelę.
| 6 lentelė | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Daugybos lentelė | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Susiję puslapiai
- Papildymas
- Kvadratinis skaičius
- Atimtis
Klausimai ir atsakymai
Klausimas: Kas yra daugyba?
Atsakymas: Daugyba yra aritmetinis veiksmas, skirtas dviejų skaičių sandaugai rasti matematikoje. Ji dažnai žymima tokiais simboliais kaip × ir ⋅.
K: Kaip vadinami du dauginami skaičiai?
A: Du dauginami skaičiai vadinami "koeficientais" arba atskirai "daugikliu" ir "daugikliu".
K: Ar daugyba yra komutatyvinė?
A: Taip, sakoma, kad skaičių daugyba yra komutatyvioji - kai skaičių eilės tvarka neturi įtakos sandaugos vertei. Tai pasakytina apie sveikuosius, racionaliuosius, realiuosius ir kompleksinius skaičius. Tačiau tai negalioja ketvertainiams, vektoriams ir matricoms.
Klausimas: Kaip galime aiškinti kardinalių skaičių daugybą?
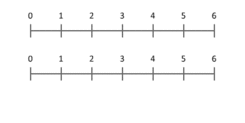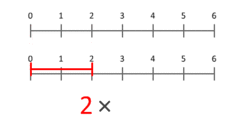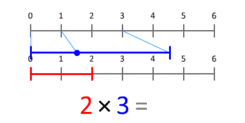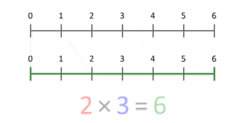
Atsakymas: Kardinaliųjų skaičių daugybą galime aiškinti kaip mastelio dydžius - kai vienas skaičius (daugiklis) masteliu keičiamas taip, kad taškas, padėtas padėtyje 1, atsidurtų tam tikrame taške (daugiklyje).
Klausimas: Kaip pavaizduoti trijų skaičių, padaugintą iš penkių?
A: Trys padauginti iš penkių gali būti užrašyti taip: 3 × 5 = 15, arba "trys kart penki yra penkiolika".
K: Kas yra priešinga daugybai?
A: Daugybos priešingybė yra dalybos.
