Vektorius: apibrėžimas, savybės ir pavyzdžiai matematikoje
Sužinokite, kas yra vektorius: aiškus apibrėžimas, pagrindinės savybės, braižymas ir praktiniai pavyzdžiai matematikoje — nuo skaliarų skirtumo iki vektorių operacijų.
Vektorius - tai matematinis objektas, turintis dydį, vadinamą dydžiu, ir kryptį.
Pavyzdžiui, vektorius naudojamas atstumui ir krypčiai parodyti. Jei paklausėte kelio ir žmogus pasakė: "Eikite vieną kilometrą į šiaurę", tai yra vektorius. Jei jis pasakytų "Eikite vieną kilometrą", nenurodydamas krypties, tai būtų skaliaras.
Vektorius paprastai braižome kaip rodykles. Rodyklės ilgis yra proporcingas vektoriaus dydžiui. Kryptis, į kurią rodo rodyklė, yra vektoriaus kryptis.
Savybės
- Ilgis (modulis): vektoriaus ilgis žymimas |v|. Pavyzdžiui, dvimačiame koordinačių plokštumoje, jei vektorius v = (x, y), jo ilgis yra |v| = sqrt(x^2 + y^2).
- Kryptis: rodo, kur vektorius nukreiptas; vektoriai su ta pačia kryptimi vadinami paraleliniais.
- Nulis (0) vektorius: neturi krypties ir turi nulį modulyje; pažymimas 0.
- Priešininkas: priešingas vektorius −v turi tą patį dydį, bet priešingą kryptį.
- Lygumas: du vektoriai lygūs, jei jie turi tą patį dydį ir tokią pačią kryptį (nepriklausomai nuo pradinio taško).
Matematinės operacijos
- Vektorių sudėtis: grafinė taisyklė — „rodyklių viršų–uodegos“ metodas; koordinatėmis, jei a = (a1, a2) ir b = (b1, b2), tada a + b = (a1 + b1, a2 + b2). Sudėtis yra komutatyvi ir asocijuojama.
- Skaliarinis dauginimas: skaliaru c dauginant vektorių v = (v1, v2) gauname cv = (c v1, c v2). Tai keičia vektoriaus ilgį (ir, jei c<0, ir kryptį).
- Skaliarinė sandauga (dot product): dvimačiame arba trimatiame euklidiniame erdvėje a·b = a1 b1 + a2 b2 (+ a3 b3, jei 3D). Ji duoda skaliarą ir naudojama kampui tarp vektorių rišti: a·b = |a||b|cosθ.
- Kryžminė sandauga (cross product) (tik 3D): a × b yra vektorius, statmenas abiems; jo modulis lygus |a||b|sinθ.
- Normalizacija: vektorių paversti vienetiniais vektoriais: u = v / |v| (jei v ≠ 0).
Pavyzdžiai
- Duomenų vektorius 2D: v = (3, 4). Jo ilgis |v| = sqrt(3^2 + 4^2) = 5. Normalizuotas vektorius u = (3/5, 4/5).
- Sudėtis: (1, 2) + (3, 1) = (4, 3).
- Skaliarinis dauginimas: 2·(1, −2) = (2, −4).
- Dot product kampui rasti: a = (1, 0), b = (0, 1) → a·b = 0 ⇒ kampas 90° (statmenas).
Vektoriai ir vektorinės erdvės
Vektorinė erdvė (pvz., R^n) yra aibė vektorių, kurioje apibrėstos sudėtis ir skaliarinis dauginimas ir kuri uždara toms operacijoms. Svarbios sąvokos:
- Linijinė kombinacija: c1 v1 + c2 v2 + ... + ck vk.
- Linijinė nepriklausomybė: vektoriai nepriklausomi, jei vienintelė linijinė kombinacija, duodanti nulį, yra visi koeficientai lygūs nuliui.
- Basis ir dimensija: bazė yra linijiškai nepriklausomų vektorių rinkinys, kuriuo išreiškiami visi erdvės vektoriai; erdvės dimensija yra bazės elementų skaičius.
Taikymas praktikoje
- Fizika: poslinkiai, greitis, pagreitis, jėgos — visi yra vektoriai.
- Inžinerija ir grafika: objektų padėtys, perstūmimai, rotacijos ir apšvietimo skaičiavimai kompiuterinėje grafikoje.
- Duomenų mokslas: elementai (atributų reikšmės) aprašomi kaip vektoriai, naudojami klasterizavimui ir mašininiam mokymuisi.
- Navigacija ir robotika: maršrutų planavimas, žingsnių vektoriai, judėjimo valdymas.
Pastabos
Vektoriaus sąvoka yra universali ir taikoma įvairiose matematikos šakose: geometrijoje, analizėje, algebroje ir funkcijų erdvėse. Praktikoje svarbu atskirti vektorių nuo skalario: skalarias matuoja tik dydis, vektoriai turi ir dydį, ir kryptį.
Vektorių pavyzdžiai
Skalarų pavyzdžiai
- Atstumas tarp dviejų vietų yra 10 kilometrų. Šis atstumas nėra vektorius, nes jame nėra krypties.
- Vaisių skaičius dėžėje nėra vektorius.
- Rodantis žmogus nėra vektorius, nes yra tik kryptis. Nėra dydžio (pavyzdžiui, atstumo nuo žmogaus piršto iki pastato).
- Objekto ilgis.
- Automobilis važiuoja 100 kilometrų per valandą greičiu. Tai neaprašo vektoriaus, nes yra tik dydis, bet nėra krypties.
Daugiau vektorių pavyzdžių
- Poslinkis yra vektorius. Poslinkis - tai atstumas, kurį kažkas juda tam tikra kryptimi. Vien tik atstumo matas yra skaliaras.
- Jėga, kuri apima kryptį, yra vektorius.
- Greitis yra vektorius, nes tai yra greitis tam tikra kryptimi.
- Pagreitis - tai greičio kitimo greitis. Objektas greitėja, jei keičia greitį arba kryptį.
Kaip pridėti vektorius
Vektorių pridėjimas popieriuje naudojant galvos ir uodegos metodą
Vektorių sudėties metodas "nuo galvos iki uodegos" yra naudingas, jei norite popieriuje apskaičiuoti dviejų vektorių sudėties rezultatą. Kaip tai padaryti:
- Kiekvienas vektorius braižomas kaip rodyklė, už kurios yra tam tikras ilgio vienetas, o kiekvienas ilgio vienetas popieriuje reiškia tam tikrą vektoriaus dydį.
- Nubraižykite kitą vektorių, kurio uodega (galas) yra ties pirmojo vektoriaus galva (priekis).
- Pakartokite tai visiems kitiems vektoriams: Nubraižykite kito vektoriaus uodegą ties ankstesnio vektoriaus galva.
- Nubrėžkite liniją nuo pirmojo vektoriaus uodegos iki paskutiniojo vektoriaus galvos - tai visų vektorių sandauga (suma).
Šis metodas vadinamas "Head to Tail" (nuo galvos iki uodegos), nes kiekviena ankstesnio vektoriaus galva veda į kito vektoriaus uodegą.
Komponentų formos naudojimas
[reikia paaiškinti d]
Komponentės formos naudojimas dviem vektoriams sudėti tiesiogine prasme reiškia, kad sudėjus vektorių komponentes sukuriamas naujas vektorius. Pavyzdžiui, tegul a ir b yra du dvimačiai vektoriai. Šiuos vektorius galima užrašyti jų komponentėmis.
a = ( a x , a y ) {\displaystyle \mathbf {a} =(a_{x},a_{y})} 
b = ( b x , b y ) {\displaystyle \mathbf {b} =(b_{x},b_{y})} 
Tarkime, kad c yra šių dviejų vektorių suma, taigi c = a + b. Tai reiškia, kad c = ( a x + b x , a y + b y ) {\displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} 
.
Pateikiame dviejų vektorių sudėties, naudojant jų sudedamąsias formas, pavyzdį.
a = ( 3 , - 1 ) {\displaystyle \mathbf {a} =(3,-1)} 
b = ( 2 , 2 ) {\displaystyle \mathbf {b} =(2,2)} 
c = a + b {\displaystyle \mathbf {c} =\mathbf {a} +\mathbf {b} } 
= ( a x + b x , a y + b y ) {\displaystyle =(a_{x}+b_{x},a_{y}+b_{y})} 
= ( 3 + 2 , - 1 + 2 ) {\displaystyle =(3+2,-1+2)} 
= ( 5 , 1 ) {\displaystyle =(5,1)} 
Šis metodas tinka visiems vektoriams, ne tik dvimačiams.
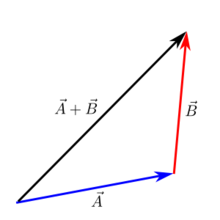
Papildymas "nuo galvos iki uodegos
Kaip dauginti vektorius
Naudojant taškinę sandaugą
Taškinė sandauga yra vienas iš vektorių daugybos būdų. Jos rezultatas yra skaliaras. Naudojama komponentų forma:
a = ( 2 , 3 ) b = ( 1 , 4 ) a ⋅ b = ( 2 , 3 ) ⋅ ( 1 , 4 ) = ( 2 ⋅ 1 ) + ( 3 ⋅ 4 ) = 2 + 12 = 14 {\displaystyle {\begin{aligned}\mathbf {a} =(2,\\\\mathbf {b} =(1,4)\\\mathbf {a} \cdot \mathbf {b} =(2,3)\cdot (1,4)\\=(2\cdot 1)+(3\cdot 4)\\=2+12=14\end{aligned}}} 
Kryžminės sandaugos naudojimas
Kryžminė sandauga yra dar vienas vektorių daugybos būdas. Taip gaunamas kitas vektorius. Naudojant komponentų formą:
a × b = | a | | | b | sin ( θ ) n {\displaystyle \mathbf {a} \ kartus \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\mathbf {n} } 
Čia | a | {\displaystyle |\mathbf {a} |} 
reiškia a {\displaystyle \mathbf {a} ilgį } 
ir n {\displaystyle \mathbf {n} } 
yra vienetinis vektorius, esantis stačiu kampu į a {\displaystyle \mathbf {a} } ir b {\displaystyle \mathbf {b} } 
.
Daugyba iš skaliarinio dydžio
Norėdami padauginti vektorių iš skaliarinio skaičiaus (įprasto skaičiaus), padauginkite skaičių iš kiekvienos vektoriaus sudedamosios dalies:
c x = ( c x 1 , c x 2 , ... , c x n ) {\displaystyle c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})} 
Pavyzdys
c = 5 x = ( 3 , 4 ) c x = ( 5 ⋅ 3 , 5 ⋅ 4 ) = ( 15 , 20 ) {\displaystyle {\begin{aligned}c=5\\\\mathbf {x} =(3,4)\\c\,\mathbf {x} =(5\cdot 3,5\cdot 4)\\=(15,20)\end{aligned}}} 
Susiję puslapiai
- Vektorinė grafika
- Vektorinis laukas
Klausimai ir atsakymai
K: Kas yra vektorius?
A: Vektorius yra matematinis objektas, turintis dydį, vadinamą dydžiu, ir kryptį. Jis dažnai vaizduojamas paryškintomis raidėmis arba kaip tiesės atkarpa iš vieno taško į kitą.
K: Kaip paprastai braižome vektorius?
A: Vektorius paprastai piešiame kaip rodykles. Rodyklės ilgis yra proporcingas vektoriaus dydžiui, o kryptis, į kurią rodo rodyklė, yra vektoriaus kryptis.
K: Ką reiškia, kai kas nors klausia kelio?
Atsakymas: Kai klausiama kelio, jei sakoma "Eikite kilometrą į šiaurę", tai būtų vektorius, bet jei sakoma "Eikite kilometrą", nenurodant krypties, tai būtų skaliaras.
K: Kokie yra keli vektorių naudojimo pavyzdžiai?
A: Vektoriai gali būti naudojami atstumui ir krypčiai parodyti. Juos taip pat galima naudoti klausiant kelio arba orientuojantis vietovėje.
K: Kaip vektoriai vaizduojami matematiškai?
A: Vektoriai dažnai vaizduojami paryškintomis raidėmis (pvz., u, v, w) arba kaip tiesės atkarpa nuo vieno taško iki kito (pvz., A→B).
K: Ką reiškia, kai kas nors vadinama skaliaru?
A: Kai kažkas vadinama skaliariniu, tai reiškia, kad nėra jokios krypties informacijos; tik skaitinės vertės, pavyzdžiui, atstumas ar greitis.
Ieškoti