Pi (π) — matematinis skaičius: apibrėžimas, reikšmė ir savybės
Atraskite Pi (π): apibrėžimas, reikšmė, iracionalumas, begaliniai skaitmenys, pagrindinės savybės, istorija ir praktiniai panaudojimai matematikoje.
Pi (arba π) yra matematinė konstanta. Tai atstumo aplink apskritimą ir apskritimo skersmens santykis. Šis santykis visada lygus tam pačiam skaičiui, nepriklausomai nuo apskritimo dydžio. Skaičius prasideda nuo 3,141592653589793... ir tęsiasi be pabaigos ir be pasikartojančio periodinio modelio — tokie skaičiai vadinami iracionaliaisiais.
Apibrėžimas ir pagrindinė savybė
Formaliai π apibrėžiamas kaip apskritimo ilgis (dar vadinamo apskritimu) padalytas iš to apskritimo skersmens. Kitaip tariant, jei C yra apskritimo ilgis, o d — skersmuo, tai C = πd. Atsižvelgiant į spindulį r (d = 2r), dažnai naudojama formulė apskritimo plotui: A = πr².
Skersmuo ir apskritimo sąvokos
Skersmuo yra didžiausia akordija, kurią galima sutalpinti į apskritimo vidų; ji eina per apskritimo centrą. Atstumas aplink apskritimą vadinamas apskritimu. Nors skirtingų apskritimų skersmuo ir apskritimo ilgis skiriasi, pi reikšmė niekada nekinta, nes apskritimo ir skersmens santykis visada yra tas pats.
Skaičiavimo būdai ir artiniai
Pi skaitmenys apskaičiuoti įvairiais būdais per istoriją. Senovėje Archimedas artino π naudodamas daugiakampius; jis apskaičiavo, kad π yra tarp 3 1/7 ir 3 10/71. Vėliau atsirado begalinės eilutės (pvz., Leibnico formulė), trigonometrijos bei sudėtingesni integralai. Modernūs skaičiavimo algoritmai, pvz., Gauss–Legendre ir Chudnovsky metodai, leidžia surasti milijardus ir trilijonus π skaitmenų.
Praktiniai artiniai: dažnai naudojami trupmenos 22/7 (≈ 3,142857...) arba tiksliau 355/113 (≈ 3,14159292...), tačiau tikslus π nėra racionalus.
Matematinės savybės
- Iracionalumas: π negali būti užrašytas kaip dviejų sveikųjų skaičių santykis; jo dešimtainė išraiška yra begalinė ir neperiodinė.
- Transcendentiškumas: π nėra jokio nenulinio polinomo su racionaliais koeficientais šaknis. Tai įrodė Ferdinand Lindemann 1882 m. Viena svarbi išvada — neįmanoma „nupiešti kvadrato“ su tokiu pačiu plotu kaip duotasis apskritimas naudojant vien tik liniuotę ir kompasą.
- Formulės: π pasirodo daugelyje sričių: geometrijoje (C = πd, A = πr²), sferose (V = 4/3 π r³, S = 4π r²), trigonometrijoje, kompleksinėje analizėje (pvz., gražioji Eulerio formulė e^{iπ} + 1 = 0) ir kt.
Pritaikymas ir kultūra
π naudojamas kasdieninėje inžinerijoje, fizikoje, signalų apdorojime, statistikoje ir daugybėje kitų sričių, kur atsiranda apskritimo ar bangų reiškiniai. Be mokslo, π turi ir populiariąją kultūrinę reikšmę: kasmet minimas Pi diena (kovo 14 d., pažymima kaip 3/14 arba 14.3), vyksta konkursai skaičiuoti π skaitmenis, kuriami meniniai projektai.
Trumpa istorija ir simbolio kilmė
Idėja apie konstantą, susijusią apskritimo ir skersmens santykiu, egzistavo senovėje įvairiose civilizacijose. Simbolį π (graik. „perimetras“ arba „periphery“ pradžioje) 1706 m. pasiūlė Williamas Jonesas, o jį išpopuliarino Leonhardas Euleris.
Pi skaitmenys prasideda: 3,141592653589793... — ir tęsiasi be pabaigos. Dėl savo unikalių savybių π liks vienas iš svarbiausių ir įdomiausių matematikos konstantų.
π = C d {\displaystyle \pi ={\frac {C}{d}}} 
(pi yra lygus apskritimo ilgiui, padalytam iš skersmens).
Pi - tai begalinė skaičių virtinė
Aproksimacija
Pi dažnai oficialiai rašoma kaip π arba graikiška raidė π kaip trumpinys. Pi taip pat yra iracionalusis skaičius, todėl jo negalima užrašyti kaip trupmenos ( a b {\displaystyle a \virš b}
), kur "a" ir "b" yra sveikieji (sveikieji) skaičiai. Tai iš esmės reiškia, kad pi skaitmenys, esantys dešinėje dešimtainio skaičiaus pusėje, amžinai nesikartoja, todėl tikslios pi reikšmės neįmanoma užrašyti kaip skaičiaus. Pi galima tik apytiksliai apskaičiuoti arba išmatuoti vertę, kuri yra pakankamai artima praktiniams tikslams.
Vertė, artima pi, yra 3,141592653589793238462643... Įprasta pi aproksimacija trupmena yra 22 7 {\displaystyle 22 \over 7}. 
, iš kurio gaunama apytiksliai 3,14285714. Ši aproksimacija yra 0,04 % nutolusi nuo tikrosios pi vertės. Nors ši aproksimacija priimtina daugeliu atvejų, kai ji naudojama realiame gyvenime, frakcija 355 113 {\displaystyle 355 \over 113}
yra tikslesnė (duoda apie 3,14159292) ir gali būti naudojama, kai reikia reikšmės, artimesnės pi. Norint gauti geresnį pi apytikslį dydį, galima naudotis kompiuteriais.
2019 m. kovą Emma Haruka Iwao apskaičiavo, kad pi vertė yra 31,4 trilijono skaitmenų.
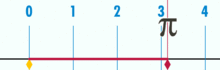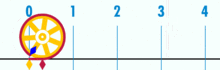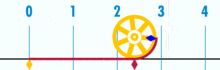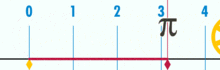
Diagrama, rodanti, kaip π galima rasti naudojant apskritimą, kurio skersmuo lygus vienetui. Šio apskritimo perimetras yra π.
Istorija
Pi reikšmė buvo žinoma senovės Indijos matematikams Bhaskaracharya ir Aryabhatta.
Matematikai jau tūkstančius metų žino apie pi, nes tiek pat laiko dirba su apskritimais. Tokios senos civilizacijos kaip babiloniečių sugebėjo apytiksliai apskaičiuoti pi iki daugelio skaitmenų, pavyzdžiui, iki trupmenos 25/8 ir 256/81. Dauguma istorikų mano, kad senovės egiptiečiai neturėjo π sąvokos ir kad šis atitikimas yra atsitiktinumas.
Pirmą kartą rašytiniuose šaltiniuose pi paminėtas 1900 m. pr. m. e. Apie 1650 m. pr. m. e. egiptietis Ahmesas Rhind papiruse nurodė reikšmę. Babiloniečiai nustatė, kad pi reikšmė yra šiek tiek didesnė už 3, paprasčiausiai padarę didelį apskritimą, prie jo perimetro ir skersmens priklijavę virvės gabalėlį, užrašę jų atstumus ir padaliję perimetrą iš skersmens.
Žinios apie skaičių pi grįžo į Europą ir pateko į hebrajų rankas, kurie šį skaičių paskelbė svarbiu Biblijos skyriuje, vadinamame Senuoju Testamentu. Vėliau dažniausiai pi buvo bandoma rasti nupiešus daug kraštinių turinčią figūrą bet kurio apskritimo viduje ir pagal figūros plotą radus pi. Pavyzdžiui, graikų filosofas Archimedas, norėdamas rasti pi reikšmę, naudojo daugiakampio formą, turinčią 96 kraštines, tačiau kinai 500 m. po Kr. sugebėjo naudoti daugiakampį, turintį 16 384 kraštines, kad rastų pi reikšmę. Graikai, pavyzdžiui, Anaksagoras iš Klazomėnų, taip pat buvo užsiėmę kitų apskritimo savybių nustatymu, pavyzdžiui, kaip iš apskritimų sudaryti kvadratus ir kvadratu apskaičiuoti skaičių pi. Nuo to laiko daugybė žmonių bandė išsiaiškinti vis tikslesnes pi reikšmes.
| Pi istorija | ||
| Filosofas | Data | Aproksimacija |
| apie 150 m. po Kr. | 3.1416 | |
| Zu Chongzhi | 430-501 M. VID. M. E. M. | 3.1415929203 |
| al-Khwarizmi | apie 800 m. po Kr. | 3.1416 |
| al-Kashi | apie 1430 m. | 3.14159265358979 |
| Viète | 1540-1603 | 3.141592654 |
| Roomen | 1561-1615 | 3.14159265358979323 |
| Van Ceulenas | apie 1600 m. | 3.14159265358979323846264338327950288 |
XVI amžiuje atsirado vis geresnių ir geresnių būdų pi rasti, pavyzdžiui, sudėtinga formulė, kurią sukūrė prancūzų teisininkas François Viète'as. Pirmą kartą graikiškas simbolis "π" buvo pavartotas 1706 m. Viljamo Džonso (William Jones) parašytoje esė.
1761 m. matematikas Lambertas taip pat įrodė, kad skaičius pi yra iracionalus, t. y. jo negalima užrašyti kaip trupmenos pagal įprastus standartus. Kitas matematikas, vardu Lindemanas, 1882 m. taip pat įrodė, kad pi priklauso grupei skaičių, vadinamų transcendentiniais skaičiais, t. y. skaičiais, kurie negali būti polinomo lygties sprendinys.
Pi taip pat galima naudoti ne tik apskritimams apskaičiuoti, bet ir daugeliui kitų dalykų. Dėl pi savybių jį galima naudoti ne tik geometrijoje, bet ir daugelyje kitų matematikos sričių, kuriose tiriamos figūros. Kai kurios iš šių sričių yra kompleksinė analizė, trigonometrija ir eilės.
Pi realiame gyvenime
Šiandien yra įvairių būdų, kaip apskaičiuoti daugelį π skaitmenų. Tačiau tai yra riboto naudojimo.
Kartais Pi gali būti naudojamas bet kurio apskritimo plotui arba apskritimo perimetrui apskaičiuoti. Apskritimo perimetrui nustatyti naudokite formulę C (perimetras) = π padauginkite iš skersmens. Norėdami rasti apskritimo plotą, naudokite formulę π (spindulys²). Ši formulė kartais užrašoma taip: A = π r 2 {\displaystyle A=\pi r^{2}}. 
, kur r yra bet kurio apskritimo spindulio kintamasis, o A yra to apskritimo ploto kintamasis.
Apskaičiuoti apskritimo perimetrą su 1 mm paklaida:
- 30 metrų spinduliui reikia 4 skaitmenų
- 10 skaitmenų, kai spindulys lygus Žemės spinduliui
- 15 skaitmenų, kai spindulys lygus atstumui nuo Žemės iki Saulės.
Kovo 14-ąją žmonės paprastai švenčia kaip Pi dieną, nes kovo 14-oji taip pat rašoma kaip 3/14, o tai reiškia pirmuosius tris skaičius 3,14 apytiksliai apskaičiuojant pi. Pi diena pradėta minėti 2001 m.
Susiję puslapiai
Klausimai ir atsakymai
K: Koks yra skaičius ً?
Atsakymas: ً yra matematinė konstanta, kuri yra apskritimo perimetro ir skersmens santykis.
K: Kas iš to gaunama?
Atsakymas: Iš to gaunamas skaičius, kuris visada yra tas pats.
K: Kaip prasideda šis skaičius?
A: Skaičius prasideda nuo 3,141592653589793... ir tęsiasi be pabaigos.
K: Kokio tipo skaičiai yra šie?
Atsakymas: Šie skaičiai vadinami iracionaliaisiais skaičiais.
K: Koks yra apskritimo skersmuo?
Atsakymas: Apskritimo skersmuo yra didžiausia akordija, kurią galima sutalpinti į apskritimą, einančią per jo centrą.
K: Kas yra apskritimo perimetras? A: Atstumas aplink apskritimą vadinamas jo apskritimu.
Klausimas: Ar pi išlieka pastovus nepriklausomai nuo skirtingų apskritimų? Atsakymas: Taip, pi išlieka pastovus nepriklausomai nuo skirtingų apskritimų, nes jų apskritimo ir skersmens santykis visada išlieka toks pat.
Ieškoti