Apskritimas — apibrėžimas, formulės, spindulys, skersmuo, plotas

Sužinokite viską apie apskritimą: aiškios apibrėžtys, formulės, spindulys, skersmuo, perimetras ir plotas su praktiniais pavyzdžiais.

Autorius: Leandro Alegsa

09-11-2025 18:53

Apskritimas yra apvali dvimatė figūra: visi apskritimo krašto taškai yra vienodai nutolę nuo centro. Centro taškas yra figūros geometrinis vidurys ir dažnai žymimas raide O.

Spindulys — tai tiesė, einanti nuo apskritimo centro iki bet kurio taško ant jo krašto. Matematikai spindulio ilgį dažniausiai žymi raide r. Spindulio reikšmė nusako, kiek „didelis“ yra apskritimas.

Skersmuo (d) yra tiesė, einanti per apskritimo centrą ir sujungusi du priešingus krašto taškus — t. y. skersmuo kerta apskritimą „per vidurį“. Skersmuo yra lygus dvigubam spindulio ilgiui:

d = 2 r {\displaystyle d=2\ r} $d=2\ r$

Apskritimo perimetras (dar vadinamas ilgumu arba aplinkos ilgiu) yra kreivė, kuri eina aplink apskritimą. Perimetrui paprastai vartojama raidė C. Svarbios formulės:

C = 2πr — perimetras išreikštas per spindulį;
C = πd — perimetras išreikštas per skersmenį.

Skaičius π (graikiška raide pi) yra konstantas, reiškiantis santykį tarp apskritimo perimetro ir jo skersmens: π = C/d. Šis santykis yra tas pats visiems apskritimams. Apytikriai reikšmės:

kaip trupmena dažnai naudojama ²²/₇ (paprasta aproksimacija);
tikslesnė trupmeninė aproksimacija — 355/113;
dešimtainė reikšmė ~ 3,141592653589793… (begalinė, neverčiama į pasikartojančią trupmeną).

Plotas (a arba dažniau A) apskritimo viduje apskaičiuojamas pagal formulę:

A = π r² — t. y. spindulys padaugintas iš savęs ir dar padaugintas iš π.

Praktinis pavyzdys: jei spindulys r = 3 vienetai, tada

C = 2πr ≈ 2 · 3,1416 · 3 ≈ 18,850 vienetų (perimetras);
A = πr² ≈ 3,1416 · 9 ≈ 28,274 kvadratinių vienetų (plotas).

Kiti svarbūs apskritimo elementai ir sąvokos:

Arka — dalis apskritimo perimetro tarp dviejų taškų.
Chorda — atkarpa, sujungusi du taškus ant apskritimo (skersmuo yra speciali chorda, kertanti centrą).
Sektorius — apskritimo dalis, ribojama dviem spinduliais ir jų tarpine arka; jo plotas lygus proporcijai iš viso apskritimo ploto pagal centrinį kampą.
Segmentas — srities tarp chordos ir atitinkamos arkos sritis.
Radianas — kampo matavimo vienetas: pilnas apskritimas yra 2π radianų, kas atitinka 360 laipsnių.

Trumpai apie formulės kilmę: santykis C/d yra pastovus visiems apskritimams — tai būtent π. Iš ten seka C = πd, o naudojant d = 2r gaunamas C = 2πr. Panašiai plotui naudojama integralinė ar geometrinė motyvacijos, kuri lemia A = πr².

Šios formulės ir sąvokos yra pagrindas analizei ir taikymui geometrijoje, trigonometrijoje, inžinerijoje ir daugelyje kitų sričių.

Ratas

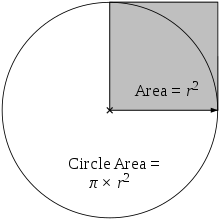
Apskritimo plotas yra lygus π pilko kvadrato ploto.

π skaičiavimas

π galima išmatuoti nubrėžus didelį apskritimą ir išmatavus jo skersmenį (d) bei apskritimą (C). Taip yra todėl, kad apskritimo perimetras visada yra π kartų didesnis už jo skersmenį.

π = C d {\displaystyle \pi ={\frac {C}{d}}} $\pi ={\frac {C}{d}}$

π taip pat galima apskaičiuoti tik matematiniais metodais. Dauguma π vertei apskaičiuoti naudojamų metodų pasižymi pageidautinomis matematinėmis savybėmis. Tačiau juos sunku suprasti nemokant trigonometrijos ir skaičiavimo. Tačiau kai kurie metodai yra gana paprasti, pavyzdžiui, ši Grigorijaus ir Leibnico eilučių forma:

π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ⋯ {\displaystyle \pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}}-{\frac {4}{7}}}+{\frac {4}{9}}-{\frac {4}{11}}}\cdots } $\pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\cdots$

Nors šią eilutę lengva užrašyti ir apskaičiuoti, nelengva suprasti, kodėl ji lygi π. Lengviau suprantamas būdas - nubrėžti įsivaizduojamą apskritimą, kurio spindulys r ir kurio centras yra pradžioje. Tada bet kuris taškas (x, y), kurio atstumas d nuo pradžios yra mažesnis už r, apskaičiuotas pagal Pitagoro teoremą, bus apskritimo viduje:

d = x 2 + y 2 {\displaystyle d={\sqrt {x^{2}+y^{2}}}} $d={\sqrt {x^{2}+y^{2}}}$

Radus apskritimo viduje esančių taškų rinkinį, galima apskaičiuoti apskritimo plotą A. Pavyzdžiui, naudojant sveikųjų skaičių koordinates dideliam r. Kadangi apskritimo plotas A yra π padaugintas iš spindulio kvadratu, π galima aproksimuoti naudojant:

π = A r 2 {\displaystyle \pi ={\frac {A}{r^{2}}}} $\pi ={\frac {A}{r^{2}}}$

Susiję puslapiai

Sfera

Klausimai ir atsakymai

K: Kas yra apskritimas?

A: Apskritimas yra apvali dvimatė figūra. Visi apskritimo krašto taškai yra vienodai nutolę nuo centro.

K: Ką matematikai naudoja apskritimo spindulio ilgiui išreikšti?

A: Matematikai apskritimo spindulio ilgiui žymėti naudoja raidę r.

K: Kas apskritimuose rašoma kaip O?

A: Apskritimo centras dažnai rašomas kaip O.

K: Kokio ilgio yra apskritimo skersmuo?

A: Apskritimo skersmuo (tai reiškia "per visą ilgį") yra tiesė, einanti iš vienos pusės į priešingą ir tiesiai per apskritimo centrą. Jis lygus dvigubam spinduliui (d lygus 2 kartus r).

K: Kokia raide matematikai žymi apskritimą?

A: Matematikai apskritimui žymėti naudoja raidę C, kuri reiškia "aplink".

K: Kaip galime apskaičiuoti apskritimo vidinį plotą?

A: Plotą A apskritimo viduje galima apskaičiuoti jo spindulį padauginus iš jo paties ir tada padauginus iš ً (A lygus ً padauginus iš r padauginus iš r).

Ieškoti