Nelygybė (matematikoje): apibrėžimas, simboliai ir pavyzdžiai
Sužinokite nelygybių apibrėžimą, simbolius (>, <, ≥, ≤) ir praktinius pavyzdžius — aiškus vadovas pradedantiesiems, moksleiviams ir matematikos entuziastams.
Nelygybė matematikoje reiškia, kad dvi reikšmės arba reiškiniai nėra lygūs ir viena iš jų yra didesnė arba mažesnė už kitą. Nelygybė gali būti griežta (kai viena pusė yra tikrai didesnė ar mažesnė) arba negriežta (kai kita reikšmė gali būti lygi arba didesnė/mažesnė).
Pagrindiniai simboliai ir jų reikšmė
- mažiau nei (a < b): a < b
reiškia, kad a yra mažesnis už b.
- daugiau nei (a > b): a > b
reiškia, kad a yra didesnis už b.
- ne mažiau nei / didesnis arba lygus (a ≥ b): a ≥ b
reiškia, kad a yra arba didesnis už, arba lygus b.
- ne daugiau nei / mažesnis arba lygus (a ≤ b): a ≤ b
reiškia, kad a yra arba mažesnis už, arba lygus b.
- nelygu (a ≠ b): reiškia, kad a nėra lygu b (tai dažnai žymi, jog reikšmės skiriasi).
Savybės ir pagrindinės taisyklės
- Transityvumas: jeigu a < b ir b < c, tai a < c. Panašiai, jeigu a ≤ b ir b ≤ c, tai a ≤ c. Jeigu mišrios: a < b ir b ≤ c, tai a < c.
- Pridėjimas/išskaičiavimas: jeigu a < b, tai a + c < b + c (pridėjus tą pačią reikšmę abiejoms pusėms, nelygybės ženklas nesikeičia).
- Dauginimas/išskaičiavimas iš skaičiaus: jeigu dauginate arba dalinate abi nelygybės puses iš teigiamo skaičiaus, ženklas lieka toks pats. Jeigu dauginama arba dalinama iš neigiamo skaičiaus, nelygybės ženklas apsiverčia (pvz., jeigu a < b ir dauginate iš -1, gaunate -a > -b).
- Sandauga su nuliu: jeigu a < b ir abi pusės dauginamos iš 0, gaunate lygybę 0 = 0 (todėl dauginti iš 0 nelygybės reikšmės prasme nėra prasminga).
- Atvirieji ir uždari intervalai: nelygybės ženklai susiję su intervalų užrašu: (a, b) reiškia a <x< b (abi galimos reikšmės atviros), [a, b] reiškia a ≤ x ≤ b (abi uždari).
Kaip sprendžiamos paprastos nelygybės — žingsniai
Bendri žingsniai sprendžiant linijinę nelygybę:
- Atlikite tas pačias aritmetines operacijas abiejose nelygybės pusėse (sudėkite arba atimkite skaičių, kad izoliuotumėte nežinomąją).
- Jeigu reikia, padalinkite arba padauginkite abi puses iš skaičiaus. Atkreipkite dėmesį į ženklą: dalinant arba dauginant iš neigiamo skaičiaus, nelygybės ženklas apsiverčia.
- Patikrinkite sprendinį (įstatykite rasti reikšmes atgal į originalią nelygybę) ir užrašykite sprendinių aibę (intervalo arba nurodydami visus galimus sprendinius).
Pavyzdžiai
- 2x + 3 < 7 → 2x < 4 → x < 2.
- -2x > 4 (dauginome/dalinome iš -1), tad padalinus iš -2 ženklas apsivers: x < -2.
- Jeigu 1 < x ≤ 4, tai x priklauso intervalui (1, 4] — atviras kairėje ir uždaras dešinėje.
- Jeigu turime a < b ir b ≤ c, tai iš transityvumo gauname a < c.
Grafinis vaizdavimas ant skaičių tiesės
Nelygybes grafiškai vaizduojamos ant skaičių tiesės: griežtos nelygybės (< arba >) žymimos tuščiomis (atviromis) žymėmis taško vietoje, o negriežtos (≤ arba ≥) — uždarais (užpildytais) taškais. Intervalai su begalybe žymimi rodyklėmis, pavyzdžiui x > 3 reiškia tašką prie 3 atviros formos ir rodyklę į dešinę.
Kiti pastebėjimai
- Nelygybių sistema: kai vienu metu tenkina keli nelygybių uždaviniai, spręsite sistemą (randama sandauga visų atskirų sprendinių aibių).
- Funkcijų lygtims ir nelygybėms taikomos papildomos technikos (kvadratinės nelygybės sprendžiamos naudojant nulinius taškus, ženklų lenteles, o racionalios nelygybės reikalauja bendrosios vardiklio analizės).
- Atkreipkite dėmesį: operacijos, kurios apima apytikslius skaičius ar srautus (pvz., logaritmai, kvadratiniai šaknys), kartais turi papildomų sąlygų sprendžiant nelygybes — būtina patikrinti, kad abi pusės būtų apibrėžtos.
Apibendrinant: nelygybės leidžia palyginti dydžius ir apibrėžti intervalus. Svarbiausios taisyklės — transityvumas, tai, kad pridedant ar daugindami iš teigiamo skaičiaus ženklas lieka, o dauginant ar dalinant iš neigiamo skaičiaus jis apsiverčia. Praktikoje svarbu rodyti žingsnius aiškiai ir tikrinti sprendinius.
Darbas su nelygybėmis
Nelygybė matematikoje yra tada, kai du sprendiniai arba atsakymai lyginami pagal didesnį nei arba mažesnį nei. Taip yra tada, kai lyginami du arba dar daug sprendinių yra nevienodo dydžio. Išspręsti nelygybę reiškia rasti jos sprendinius. Kai į kintamąjį įrašome skaičių ir teiginys yra teisingas, tai yra sprendinys. Kai į kintamąjį pakeičiate skaičių ir teiginys nėra teisingas, tada šis skaičius nėra teiginio sprendinys.
Nelygybė - tai duotojo kintamojo sprendinio radimas. Tai santykinės aibės tvarkos radimas. Nelygybė turi daug sprendinių, tačiau reikia rasti tikruosius sprendinius. Nelygybė yra realiųjų skaičių sprendiniai. Tinkamas nelygybės skaitymo būdas yra iš kairės į dešinę, kaip ir kitų lygčių, tačiau vienintelis skirtumas yra tas, kad kiekvienai lygčiai jos turi skirtingas taisykles.
Pavyzdžiui, x+4>12, kur x yra realusis skaičius. Pirmiausia reikia rasti x ir sužinoti, ar tai yra sprendinys. Atsakymas bus x>8 ir tai yra teisingas teiginys. Ši išraiška yra apie x vietą realiųjų skaičių aibėje. Vienas iš būdų parodyti vietą visų kitų realiųjų skaičių atžvilgiu yra skaičių tiesė (žr. 1 paveikslą Nelygybė).
.jpg)
1 nelygybė Tai yra lygties x+4>12 sprendinys
Įvairių rūšių nelygybės
Yra penkios skirtingos nelygybės rūšys:
- Pirmoji yra tiesinė nelygybė, kuri yra nelygybė, diferencijuojanti išraiškas mažesnes už arba lygias, mažesnes už arba didesnes už, didesnes už, didesnes už. Tai tokia, kurią pakeitus nelygybe lygybės santykiu, gautas rezultatas bus tiesinė lygtis.
- Antrasis yra nelygybių deriniai, kurie yra patenkinti nelygybės, jūs turite turėti skaičių sprendinių rinkinių taip, kad skaičiai patenkinti nelygybės bus reikšmės dviejų sprendinių rinkinių kryžminimo.
- Trečioji - nelygybės, apimančios absoliučiuosius dydžius, o tai reiškia, kad reikšmes galima performuluoti kaip nelygybių, apimančių absoliučiuosius dydžius, derinius.
- Ketvirtoji vadinama polinomine nelygybe reiškia, kad ji yra tolydi, tai reiškia, kad jų grafai neturi jokių šuolių ar pertraukų.
- Paskutinė, bet ne mažiau svarbi yra racionalioji nelygybė, kuri reiškia, kad tai yra vieno iš daugianariųjų dalijamo daugianario forma. Kitaip tariant, racionaliosios funkcijos grafikai neturi jokių lūžių ir nevaizduoja ties vardiklio nuliais.
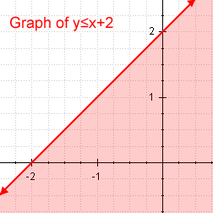
Tiesinė nelygybė Tiesinės nelygybės pavyzdys
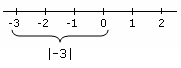
absoliutinė vertė Pavyzdys, rodantis absoliučiąją vertę
Keturi nelygybių sprendimo būdai
Yra keturi būdai kvadratinėms lygtims spręsti:
- Pirmoji taisyklė - abiejose pusėse turite pridėti arba atimti tą patį skaičių.
- Antroji taisyklė yra ta, kad turite perkelti puses ir pakeisti nelygybės ženklo padėtį.
- Trečioji taisyklė - reikia dauginti.
- Ketvirtoji taisyklė - tą patį teigiamą arba neigiamą skaičių padalyti į abi puses. Tačiau jas galima naudoti tik sprendžiant lengvus nelygybės uždavinius.
Be to, nelygybei išspręsti prireiks dviejų žingsnių. Pirmasis - supaprastinimas naudojant sudėjimo arba atimties atvirkštinę reikšmę. Antrasis - supaprastinti dar labiau, naudojant daugybos arba dalybos atvirkštinę reikšmę. Daugindami arba dalydami nelygybę iš neigiamo skaičiaus, nepamirškite pasukti nelygybės simbolio.

Nelygybių pridėjimo pavyzdys.

nelygybės dauginimo pavyzdys
Pavyzdžiai, kaip spręsti nelygybes
Nelygybė - tai matematinis teiginys, paaiškinantis, kad dvi reikšmės nėra lygios ir skirtingos. Lygtis ab reiškia, kad a nelygus b. Nelygybė yra tokia pati kaip ir bet kuri lygtis, tačiau skiriasi tik tuo, kad nelygybėje nenaudojamas lygybės ženklas, o naudojami simboliai. Nelygybė b>a reiškia, kad b yra didesnis už a. Greičio ribojimams, žymėjimui ir kt. išreikšti naudojama nelygybė.
Spręsdamas nelygybę žmogus turi turėti teisingą teiginį. Kai dalijate arba dauginate nelygybę su neigiamu skaičiumi abiejose pusėse, teiginys yra neteisingas. norint, kad teiginys būtų teisingas su neigiamu skaičiumi, reikia pakeisti simbolį, kad tas teiginys būtų teisingas. Kai skaičius yra teigiamas, simbolio apversti nereikia. Nelygybė yra susijusi su teisingo teiginio sudarymu.
Pavyzdžiui, pradėkite nuo teisingo teiginio -6y<-12. Kai abi puses padalysime iš -6, gausime rezultatą y< 2. Šiame teiginyje simbolis turi būti sukeistas vietomis, kad būtų teisingas teiginys, y>2 yra teisingas atsakymas. Skaičių eilutėje (žr. 2 pav. nelygybė) uždaras užbrūkšniuotas apskritimas nurodo, kad jis įtrauktas į sprendinių aibę. Atviras apskritimas rodo, kad jis neįtrauktas į sprendinių aibę.
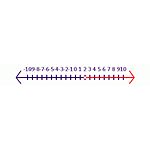
2 nelygybė Lygties -6y<-12 sprendimas
Susiję puslapiai
- Lygybė (matematika)
- Lygtis
Klausimai ir atsakymai
K: Ką reiškia "a < b"?
A: Tai reiškia, kad a yra mažesnis už b.
K: Ką reiškia "a > b"?
A: Tai reiškia, kad a yra didesnis už b.
K: Ką reiškia "a ≥ b"?
A: Tai reiškia, kad a nėra mažesnis už b, t. y. jis yra arba didesnis, arba lygus b.
K: Ką reiškia "a ≤ b"?
A: Tai reiškia, kad a nėra didesnis už b, arba jis yra mažesnis už b, arba jam lygus.
K: Kaip nelygybė gali būti naudojama matematikoje?
Atsakymas: Nelygybė gali būti naudojama teiginiui, kad viena išraiška yra mažesnė, didesnė, ne mažesnė arba ne didesnė už kitą, pavadinti.
Ieškoti