Matmenys -
Matmenys - tai būdas, kuriuo matome, matuojame ir patiriame savo pasaulį. Naudojant aukštyn ir žemyn, iš dešinės į kairę, iš nugaros į priekį, karšta ir šalta, kaip sunkus ir kaip ilgas, taip pat daugiau pažangių sąvokų iš matematikos ir fizikos. Vienas iš būdų apibrėžti matmenį - pažvelgti į laisvės laipsnius arba į tai, kaip objektas gali judėti tam tikroje erdvėje. Yra įvairių sąvokų arba būdų, kuriais vartojama sąvoka matmuo, taip pat yra įvairių apibrėžčių. Nėra apibrėžties, kuri atitiktų visas sąvokas.
Vektorinėje erdvėje (vektorius yra atvira linija) matmuo yra lygus vektorių arba linijų krypčių kardinalumui arba skaičiui. Jis taip pat yra lygus didžiausios tos erdvės tiesių krypčių grupės skaičiui. "Įprasti" kasdienio gyvenimo objektai apibūdinami trimis matmenimis, kurie paprastai vadinami ilgiu, pločiu ir gyliu. Matematikai šią sąvoką vadina euklidine erdve.
Matmenys gali būti naudojami ir padėčiai matuoti. Atstumas iki pozicijos nuo pradinės vietos gali būti matuojamas ilgio, pločio ir aukščio kryptimis. Šie atstumai yra padėties matas.
Kartais įvykio padėčiai laike ir erdvėje parodyti naudojamas ketvirtasis (4D) matmuo - laikas.
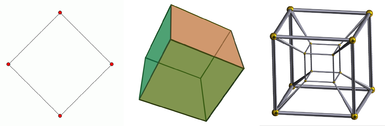
Iš kairės į dešinę: kvadratas, kubas ir teseraktas. Kvadratas yra dvimatis objektas, kubas - trimatis objektas, o teseraktas - keturmatis objektas. Vienmatis objektas yra tik linija. Pateikiama kubo projekcija, nes į jį žiūrima dvimačiame ekrane. Tas pats pasakytina ir apie teseraktą, kuris papildomai gali būti rodomas tik kaip projekcija net ir trimatėje erdvėje.
Pirmųjų keturių erdvinių matmenų schema.
Kiti matmenys
Šiuolaikiniame moksle žmonės naudoja kitus matmenis. Tokie matmenys, kaip temperatūra ir svoris, gali būti naudojami norint parodyti ko nors padėtį ne tokiose paprastose erdvėse. Mokslininkai šiuos matmenis tiria naudodami matmenų analizę.
Matematikai taip pat naudoja matmenis. Matematikoje matmenys yra bendresni. Matematikos matmenys gali nematuoti daiktų pasaulyje. Matematikos aritmetikos su matmenimis taisyklės gali skirtis nuo įprastų aritmetikos taisyklių.
Matmenys ir vektoriai
Vektoriai naudojami atstumams ir kryptims parodyti. Vektoriai dažnai naudojami inžinerijoje ir gamtos moksluose, o kartais ir matematikoje.
Vektorius yra skaičių sąrašas. Kiekvienai dimensijai tenka po vieną skaičių. Vektoriams taikomos aritmetinės taisyklės.
Pavyzdžiui, jei Džeinė nori sužinoti Salės padėtį, Salė gali pateikti Džeinei vektorių, rodantį padėtį. Jei Džeinė ir Salė yra pasaulyje, yra trys matmenys. Todėl Sally pateikia Džeinei trijų skaičių sąrašą, kad parodytų jos padėtį. Trys skaičiai vektoriuje, kurį Sally pateikia Jane, gali būti tokie:
- Sally atstumas į šiaurę nuo Jane
- Sally atstumas į rytus nuo Jane
- Sally ūgis virš Jane
Klausimai ir atsakymai
K: Kas yra dimensija?
A: Matmuo - tai būdas matuoti, matyti ir patirti pasaulį naudojant tokias sąvokas kaip aukštyn ir žemyn, iš dešinės į kairę, iš nugaros į priekį, karšta ir šalta, kaip sunku ir kaip ilgai. Jis taip pat gali būti apibrėžiamas kaip laisvės laipsniai arba būdas, kuriuo objektas gali judėti tam tikroje erdvėje.
Klausimas: Kaip matematikai apibrėžia euklidinę erdvę?
A: Matematikai euklidinę erdvę apibrėžia kaip erdvę, kurią apibūdina trys matmenys, paprastai vadinami ilgiu, pločiu ir gyliu.
K: Koks yra vektorių skaičius vektorinėje erdvėje?
A: Vektorių skaičius vektorinėje erdvėje yra lygus jos bazinės aibės kardinalumui (arba vektorių skaičiui).
K: Kiek matmenų naudojama padėčiai matuoti?
A: Padėčiai matuoti naudojami trys matmenys (ilgis, plotis ir aukštis). Kai kuriais atvejais gali būti naudojamas ketvirtasis (4D) matmuo - laikas - siekiant parodyti įvykio padėtį laike ir erdvėje.
K: Ką reiškia dim(V)?
A: Dim(V) reiškia V matmenį, kuris yra lygus jo bazinės aibės kardinalumui (arba vektorių skaičiui) arba jo tiesių krypčių skaičiui.
K: Ar yra vienas apibrėžimas, kuris atitinka visas su matmenimis susijusias sąvokas?
Atsakymas: Ne, nėra vieno apibrėžimo, kuris atitiktų visas su matmenimis susijusias sąvokas.
