Algebra: apibrėžimas, pagrindai ir taikymai
Algebra: aiškus apibrėžimas, pagrindinės taisyklės ir praktiniai taikymai kasdieniame gyvenime, inžinerijoje bei programavime — suprantamai ir su pavyzdžiais.
Algebra (iš arabų kalbos: الجبر, išvertus „al‑jabr“, reiškianti „suardytų dalių sujungimas“) yra matematikos dalis. Ji nagrinėja skaičių, simbolių ir kintamųjų išraiškas bei taisykles, kuriomis remiantis galima jas manipuliuoti, supaprastinti ir spręsti uždavinius. Jungtinėse Amerikos Valstijose ši sritis dažnai vadinama matematika, Jungtinėje Karalystėje - maths arba numeracy. Algebros simboliai leidžia trumpai ir aiškiai užrašyti santykius, ryšius bei dėsningumus, kurie pasitaiko tiek matematikoje, tiek gyvenime.
Pagrindinės sąvokos
Algebroje dažnai sutinkamos šios sąvokos:
- Kintamieji — simboliai (dažniausiai raidės), kurie žymi nežinomas arba keičiantįs reikšmes (kintamieji).
- Konstantos — fiksuotos reikšmės (pvz., 2, −5, π).
- Išraiškos — kombinacijos iš kintamųjų ir konstantų, pvz., 3x + 2.
- Lygtys — teiginiai, kuriuose dvi išraiškos yra lygios (žymima =); sprendimas yra kintamųjų reikšmės, tenkinančios tą lygybę (lygtis).
- Nelygybės — rodo santykį „mažiau nei“, „daugiau nei“ ar jiems lygius santykius (nelygybės), pvz., x < 5 arba y ≥ 0.
- Funkcijos — taisyklės, kurios kiekvienai įvesties reikšmei priskiria vieną išvesties reikšmę; dėl to jas patogu vaizduoti grafikuose.
Paprastas pavyzdys ir sprendimas
Jei turime paprastą lygtį: 2 + 3 = x. Tuomet sprendimas yra x = 5, kitaip tariant „x lygus penkiems“. Tokia reikšmė vadinama sprendimu.
Algebros taisyklės ir operacijos
Algebroje naudojami skaičių ir simbolių tarpusavio santykiai bei pagrindiniai aritmetiniai veiksmai:
- Skaičių taisyklės ir keturi pagrindiniai veiksmai: sudėtis, atimtis, daugyba ir dalyba.
- Sudėtingesnės operacijos: laipsniai ir eksponentai, pvz., kvadratai ir kvadratinės šaknys.
- Algebros dėsniai: komutatyvumas (a + b = b + a), asociatyvumas ((a + b) + c = a + (b + c)), distributyvumas (a(b + c) = ab + ac) — šie dėsniai leidžia supaprastinti išraiškas ir spręsti lygtis.
- Tvarka atlikti veiksmus (Pirmumas laipsniams, daugybai, dalybai, sudėčiai ir atimčiai) padeda išvengti klaidų skaičiuojant sudėtingesnes išraiškas.
Lygtis ir nelygybės — tipai ir sprendimo metodai
Algebra tradiciškai taikoma lygtims ir nelygybėms spręsti. Dažniausios lygtžių rūšys:
- Tiesinės lygtys — pavyzdžiui, tiesės lygtis y=mx+b; sprendžiamos algebraiškai arba grafikais (tiesinės lygtys).
- Kvadratinės lygtys — turi laipsnį 2 (kintamasis kartojasi dukart), jų sprendimo metodai: faktorizacija, kvadratinės formulės taikymas arba pabaidymas (kvadratinės lygtys).
- Polinominės lygtys — aukštesnių laipsnių lygtys, kuriose gali prireikti faktorizacijos ar skaitinio sprendimo.
- Lygčių sistemos — kelių lygių tūrinės sistemos, sprendžiamos eliminavimo, pakeitimo arba matricų metodais.
Funkcijos ir grafikai
Funkcija f(x) priskiria kiekvienai x reikšmei tam tikrą f(x). Grafikais (pvz., koordinačių plokštumoje) aiškiai matomi ryšiai tarp kintamųjų ir leidžiama analizuoti tokius dalykus kaip nulinės reikšmės, ekstremumai ar asimptotos. Dėl to algebra yra svarbi analizei, geometrijai ir modeliavimo uždaviniams.
Taikymai kasdieniame gyvenime ir moksle
Algebra yra plačiai taikoma praktiškai visuose mokslo ir inžinerijos srityse. Ji naudojama formuluojant ir sprendžiant realius uždavinius, nes skaičiais ir simboliais galima išreikšti realių dalykų kiekius ir santykius. Pavyzdžiai:
- Fizikoje — judėjimo lygtis, energijos ir jėgos skaičiavimai.
- Inžinerijoje — konstrukcijų stiprumas, signalo analizė, sistemos projektavimas.
- Kompiuterių programavime — algoritmų analizė, kriptografija, duomenų modeliavimas.
- Praktinės profesijos: geodezija, statyba, verslas ir ypač buhalterija — visur reikalingas skaičiavimų ir modelių supratimas.
Platesnė perspektyva: nuo simbolinės algebros iki abstrakčiosios algebros
Paprastoji algebra (kartais vadinama elementariąja) sprendžia lygtis ir tvarko simbolius pagal taisykles. Aukštesniame lygyje vystėsi abstrakčioji algebra, kurioje nagrinėjami struktūriniai objektai — grupės, žiedai, laukai ir modulių sistemos. Šios sritys yra pagrindas teorinei matematikai ir turi taikymų kriptografijoje, kodų teorijoje bei kitose disciplinose.
Kaip mokytis algebros efektyviau
- Pradėkite nuo aiškios simbolių reikšmių supratimo ir nuo paprastų išraiškų supaprastinimo.
- Praktikuokite pagrindines taisykles (distributyvumas, komutatyvumas, asociatyvumas) ir tvarką atlikti veiksmus.
- Spręskite pavyzdžius žingsnis po žingsnio: supaprastinimas → pertvarkymas → faktorizacija → sprendimas.
- Naudokite grafikus, kad vizualizuotumėte funkcijų elgseną ir patikrintumėte sprendimus.
Apibendrinant: algebra yra galingas įrankis, leidžiantis abstraktiai apibūdinti skaitinius santykius ir spręsti tiek paprastus, tiek sudėtingus uždavinius įvairiose mokslo ir praktikos srityse.
Istorija
Ankstyvąsias algebros formas sukūrė babiloniečiai ir graikų geometrai, pavyzdžiui, Aleksandrijos Herojus. Tačiau žodis "algebra" yra lotyniška arabiško žodžio Al-Jabr ("liejimas") forma ir kilęs iš matematikos knygos Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah ("Esė apie liejimo ir lygties skaičiavimą"), kurią IX a. parašė persų matematikas Muhammadas ibn Mūsā al-Khwārizmī, musulmonas, gimęs Chvarizme, Uzbekistane. Jis klestėjo pas Al-Ma'mouną Bagdade, Irake, 813-833 m. ir mirė apie 840 m. XII a. knyga buvo atgabenta į Europą ir išversta į lotynų kalbą. Tuomet knyga buvo pavadinta "Algebra". (Matematiko vardo galūnė al-Khwarizmi buvo pakeista į žodį, kurį lengviau ištarti lotyniškai, ir tapo anglišku žodžiu algorithm).
Pavyzdžiai
Pateikiame paprastą algebros uždavinio pavyzdį:
Sue turi 12 saldainių, o Ann - 24 saldainius. Jos nusprendžia pasidalyti, kad turėtų tiek pat saldainių. Kiek saldainių turės kiekviena iš jų?
Šiais veiksmais galite išspręsti šią problemą:
- Norėdama turėti tiek pat saldainių, Ann turi atiduoti dalį jų Sue. Tegul x reiškia saldainių skaičių, kurį Ann duoda Sue.
- Sue saldainiai plius x turi būti tokie patys kaip Ann saldainiai minus x. Tai užrašoma taip: Tai rašoma taip: 12 + x = 24 - x
- Iš abiejų lygties pusių atimkite 12. Gauname: x = 12 - x. (Tai, kas vyksta vienoje lygybės ženklo pusėje, turi vykti ir kitoje pusėje, kad lygtis išliktų teisinga. Taigi šiuo atveju, kai iš abiejų pusių buvo atimta 12, atsirado vidurinis žingsnis 12 + x - 12 = 24 - x - 12. Kai žmogui tai jau patogu, vidurinysis žingsnis nerašomas).
- Prie abiejų lygties pusių pridėkite x. Gauname: 2x = 12
- Abi lygties puses padalykite iš 2. Gauname x = 6. Atsakymas yra šeši. Jei Ann duos Sue 6 saldainius, jos turės tiek pat saldainių.
- Norėdami tai patikrinti, į pradinę lygtį, kurioje buvo x, vėl įrašykite 6: 12 + 6 = 24 - 6
- Gauname 18=18, o tai yra tiesa. Dabar kiekvienas iš jų turi po 18 saldainių.
Pasipraktikavus algebrą galima naudoti, kai susiduriama su problema, kurią per sunku išspręsti kitais būdais. Tokioms problemoms, kaip greitkelio tiesimas, mobiliojo telefono projektavimas ar vaistų nuo ligų paieška, spręsti reikia algebros.
Algebros rašymas
Kaip ir daugelyje matematikos sričių, z pridėjimas prie y (arba y plius z) užrašomas kaip y + z. Z atimtis iš y (arba y minus z) užrašoma kaip y - z. Y dalijimas iš z (arba y per z: y z {\displaystyle y \over z} 
) užrašomas kaip y ÷ z arba y/z. Dažniau vartojama y/z.
Algebroje y padauginus iš z (arba y padauginus iš z) galima užrašyti keturiais būdais: y × z, y * z, y-z arba tiesiog yz. Daugybos simbolis "×" paprastai nenaudojamas, nes jis per daug panašus į raidę x, kuri dažnai naudojama kaip kintamasis. Be to, dauginant didesnę išraišką, galima naudoti skliaustelius: y (z+1).
Kai algebroje dauginame skaičių ir raidę, prieš raidę rašome skaičių: 5 × y = 5y. Kai skaičius yra 1, 1 nerašoma, nes 1 padaugintas iš bet kokio skaičiaus yra tas skaičius (1 × y = y), todėl jo nereikia.
Be to, algebroje nereikia naudoti x arba y raidžių. Kintamieji yra tik simboliai, reiškiantys nežinomą skaičių arba vertę, todėl galite naudoti bet kurį kintamąjį.
Funkcijos ir grafikai
Svarbi algebros dalis yra funkcijų nagrinėjimas, nes funkcijos dažnai atsiranda lygtyse, kurias bandome išspręsti. Funkcija - tai tarsi mašina, į kurią galima įdėti skaičių (ar skaičius) ir gauti tam tikrą skaičių (ar skaičius). Naudojant funkcijas, grafikai gali būti galingi įrankiai, padedantys tirti lygčių sprendinius.
Grafikas - tai paveikslas, kuriame pavaizduotos visos kintamųjų reikšmės, dėl kurių lygtis ar nelygybė yra teisinga. Paprastai tai lengva padaryti, kai yra tik vienas ar du kintamieji. Dažnai grafikas yra tiesė, ir jei ji nėra vingiuota arba neina tiesiai aukštyn-žemyn, ją galima aprašyti pagrindine formule y = mx + b. Kintamasis b yra grafiko y intercepcija (vieta, kur tiesė kerta vertikaliąją ašį), o m - tiesės nuolydis arba statumas. Ši formulė taikoma grafiko koordinatėms, kai kiekvienas tiesės taškas užrašomas (x, y).
Kai kuriuose matematikos uždaviniuose, pvz., tiesės lygtyje, gali būti daugiau nei vienas kintamasis (šiuo atveju x ir y). Norint rasti tiesės taškus, keičiamas vienas kintamasis. Keičiamas kintamasis vadinamas nepriklausomu kintamuoju. Tuomet atliekami matematiniai skaičiavimai, kad gautume skaičių. Gautas skaičius vadinamas priklausomu kintamuoju. Dažniausiai nepriklausomas kintamasis užrašomas kaip x, o priklausomas kintamasis - kaip y, pvz., y = 3x + 1. Tai dažnai vaizduojama grafike, naudojant x ašį (einančią į kairę ir į dešinę) ir y ašį (einančią į viršų ir į apačią). Jį taip pat galima užrašyti funkcijos pavidalu: f(x) = 3x + 1. Taigi šiame pavyzdyje kaip x galime įrašyti 5 ir gauti y = 16. Jei į x įrašytume 2, gautume y = 7. O įrašius 0 už x gautume y=1. Taigi per taškus (5,16), (2,7) ir (0,1) eitų tiesė, kaip parodyta dešinėje esančiame grafike.
Jei x turi galybę 1, tai yra tiesė. Jei ji yra kvadratas arba kita galybė, ji bus kreiva. Jei joje naudojama nelygybė (< arba > ), paprastai dalis grafiko būna šešėliuojama - virš arba po tiesės.
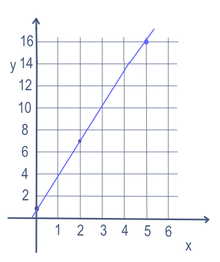
Tiesinė lygtis y=3x+1
Algebros taisyklės
Algebroje yra kelios taisyklės, kuriomis galima vadovautis norint geriau suprasti lygtis. Jos vadinamos algebros taisyklėmis. Nors šios taisyklės gali atrodyti beprasmiškos ar akivaizdžios, pravartu suprasti, kad šios savybės galioja ne visose matematikos šakose. Todėl prieš priimant šias aksiomines taisykles kaip savaime suprantamą dalyką bus naudinga žinoti, kaip jos deklaruojamos. Prieš pereidami prie taisyklių, apmąstykite du apibrėžimus, kurie bus pateikti.
- Priešingas - priešingas {\displaystyle a}
yra - a {\displaystyle -a} 
. - Reciprocal - a {\displaystyle a} abipusė reikšmė yra 1 a {\displaystyle {\frac {1}{a}}}
.
Taisyklės
Komutatyvinė sudėties savybė
"Komutatyvinė" reiškia, kad sukeitus skaičius vietomis gaunamas tas pats rezultatas. Kitaip tariant, lygties narių eiliškumas neturi reikšmės. Kai dviejų narių operatorius yra sudėtis, taikoma "komutatyvinė sudėties savybė". Algebros terminais tai reiškia, kad a + b = b + a {\displaystyle a+b=b+a} 
.
Atkreipkite dėmesį, kad tai netaikoma atimties atveju! (t. y. a - b ≠ b - a {\displaystyle a-b\neq b-a} 
)
Komutatyvinė daugybos savybė
Kai dviejų narių operatorius yra daugyba, taikoma "komutatyvinė daugybos savybė". Algebriškai tai reiškia, kad a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} 
.
Atkreipkite dėmesį, kad tai netaikoma dalijimui! (t. y. a b ≠ b a {\displaystyle {\frac {a}{b}}}neq {\frac {b}{a}}}}). 
kai a ≠ b {\displaystyle a\neq b} 
)
Asociatyvioji sudėties savybė
"Asocijuotas" reiškia skaičių grupavimą. Asociatyvioji sudėties savybė reiškia, kad, sudedant tris ar daugiau narių, nesvarbu, kaip šie nariai sugrupuoti. Algebriškai tai reiškia, kad a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} 
. Atkreipkite dėmesį, kad tai negalioja atimties atveju, pvz., 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1} 
(žr. skirstinio savybę).
Asociatyvioji daugybos savybė
Asociatyvioji daugybos savybė reiškia, kad dauginant tris ar daugiau narių nesvarbu, kaip šie nariai sugrupuoti. Algebriniu požiūriu gauname a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c} 
. Atkreipkite dėmesį, kad tai negalioja dalijimo atveju, pvz., 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2} 
.
Paskirstomoji savybė
Paskirstomoji savybė teigia, kad skaičiaus daugyba iš kito nario gali būti paskirstyta. Pavyzdžiui: a ⋅ ( b + c ) = a b + a c {\displaystyle a\cdot (b+c)=ab+ac} 
. (Nepainiokite to su asociatyviosiomis savybėmis! Pavyzdžiui, a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\displaystyle a\cdot (b+c)\neq (a\cdot b)+c} 
.)
Adityvioji tapatybės savybė
"Tapatumas" reiškia skaičiaus savybę, kad jis yra lygus sau pačiam. Kitaip tariant, egzistuoja tokia dviejų skaičių operacija, kad jis būtų lygus sumos kintamajam. Adityvinė tapatumo savybė teigia, kad bet kurio skaičiaus ir 0 suma yra tas skaičius: a + 0 = a {\displaystyle a+0=a} 
. Tai galioja ir atimant: a - 0 = a {\displaystyle a-0=a} 
.
Daugiamačio tapatumo savybė
Daugiamačio tapatumo savybė teigia, kad bet kurio skaičiaus ir 1 sandauga yra tas skaičius: a ⋅ 1 = a {\displaystyle a\cdot 1=a} 
. Tai taip pat galioja ir dalijimui: a 1 = a {\displaystyle {\frac {a}{1}}=a} 
.
Adityvioji atvirkštinė savybė
Adityvioji atvirkštinė savybė yra tarsi priešinga adityviajai tapatybės savybei. Kai operacija yra skaičiaus ir jam priešingo skaičiaus suma ir ji lygi 0, ši operacija yra galiojanti algebrinė operacija. Algebriniu požiūriu ji teigia: a - a = 0 {\displaystyle a-a=0} 
. Adityvioji atvirkštinė 1 reikšmė yra (-1).
Daugiamačio atvirkštinė savybė
Daugiamačio atvirkštinė savybė reiškia, kad kai operacija yra skaičiaus ir jo atvirkštinio sandauga ir yra lygi 1, ši operacija yra galiojanti algebrinė operacija. Algebriniu požiūriu ji teigia: a a = 1 {\displaystyle {\frac {a}{a}}=1} 
. Daugiamačiai atvirkštinė 2 reikšmė yra 1/2.
Išplėstinė algebra
Be "elementariosios algebros", arba pagrindinės algebros, kolegijose ir universitetuose dėstomos pažangios algebros formos, tokios kaip abstrakčioji algebra, tiesinė algebra ir universalioji algebra. Į jas įeina ir tai, kaip naudoti matricą daugeliui tiesinių lygčių vienu metu spręsti. Abstrakčioji algebra - tai lygtyse esančių dalykų tyrimas, neapsiribojant vien skaičiais, o pereinant prie abstraktesnių dalykų su skaičių grupėmis.
Daugelis matematikos uždavinių yra susiję su fizika ir inžinerija. Daugelyje šių fizikos uždavinių laikas yra kintamasis. Laikas žymimas raide t. Naudojant pagrindines algebros idėjas galima sumažinti matematinį uždavinį iki paprasčiausios formos, todėl lengviau spręsti sudėtingus uždavinius. Energija yra e, jėga - f, masė - m, pagreitis - a, o šviesos greitis kartais yra c. Tai naudojama kai kuriose garsiose lygtyse, pavyzdžiui, f = ma ir e = mc^2 (nors pastarajai lygčiai sudaryti reikėjo sudėtingesnių matematinių skaičiavimų nei algebra).
Susiję puslapiai
- Matematikos temų sąrašas
- Veiksmų eiliškumas
- Parabolė
- Kompiuterinės algebros sistema
Klausimai ir atsakymai
K: Kas yra algebra?
A: Algebra yra matematikos dalis, kurioje kintamieji naudojami dar nežinomai vertei išreikšti.
K: Ką algebroje reiškia lygybės ženklas?
A: Lygybės ženklas (=) algebroje reiškia lygtį.
K: Kas algebroje yra funkcija?
A: Algebroje funkcija yra ypatinga lygties rūšis, kuri visada vieną įvestį paverčia vienu išėjimu.
K: Kaip algebra gali būti naudojama sprendžiant realias problemas?
A: Algebra gali būti naudojama realioms problemoms spręsti, nes algebros taisyklės veikia realiame gyvenime, o skaičiais galima išreikšti realių dalykų vertes. Fizikoje, inžinerijoje ir kompiuterių programavime algebra naudojama nuolat. Ją taip pat naudinga išmanyti geodezijoje, statyboje ir versle, ypač buhalterijoje.
Klausimas: Kokie matematiniai veiksmai su skaičiais naudojami algebroje?
A: Algebroje žmonės naudoja skaičių taisykles ir matematinius veiksmus, tokius kaip skaičių sudėjimas, atimtis, daugyba ir dalyba. Sudėtingesni veiksmai susiję su eksponentais, pradedant kvadratais ir kvadratinėmis šaknimis.
K: Kokie yra algebroje naudojamų lygčių pavyzdžiai?
A: Algebroje naudojamų lygčių pavyzdžiai yra tiesinės lygtys (tiesės lygtis) ir kvadratinės lygtys, kurių kintamieji yra kvadratai (padauginti iš savęs).
Ieškoti