Elementarioji algebra: apibrėžimas, pagrindinės sąvokos ir taikymai

Elementarioji algebra: aiškus apibrėžimas, pagrindinės sąvokos, lygties sprendimas ir praktiniai taikymai moksle, versle bei kasdienėse situacijose.

Autorius: Leandro Alegsa

28-01-2026 23:30

Elementarioji algebra - tai paprasčiausia algebros forma, kurios mokiniai mokomi. Dažnai tai yra viena iš kitų matematikos sričių, kurios mokiniai mokomi po aritmetikos. Aritmetikoje pasitaiko tik skaičiai ir tokie operatoriai kaip +, -, × ir ÷; algebroje kintamieji (pvz., a, x, y) naudojami skaičiams žymėti. Tai naudinga, nes:

Ji leidžia žmonėms spręsti nežinomų skaičių problemas. Tai reiškia, kad reikia mokytis apie lygtis ir kaip jas spręsti (pavyzdžiui, "raskite skaičių x, kai 3 x + 1 = 10 {\displaystyle 3x+1=10} $3x+1=10$ ").
Tai leidžia apibendrinti aritmetikos taisykles. Kai kurie mokiniai supranta, kad 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3}. $3+4=4+3$ , tai padeda įrodyti, kad a + b = b + a {\displaystyle a+b=b+a} visiems a ir b. Dėl to algebra yra geras žingsnis mokantis abstrakcijos (bendrųjų idėjų mokymosi iš daugelio pavyzdžių).
Jis padeda žmonėms suprasti ir kurti funkcinius ryšius (kartais dar vadinamus priežasties ir pasekmės). Pavyzdys: "Jei bus parduota x bilietų, pelnas bus 3 x - 10 {\displaystyle 3x-10} $3x-10$ dolerių".

Šie trys dalykai yra pagrindinės elementariosios algebros kryptys. Elementarioji algebra dažnai naudojama daugelyje kitų dalykų, pavyzdžiui, mokslo, verslo ir statybos. Abstrakčioji algebra, daug sudėtingesnė tema, paprastai dėstoma vėlai kolegijoje.

Pagrindinės sąvokos

Kintamieji – simboliai (dažniausiai raidės), žymintys nežinomus arba kintančius skaičius. Pvz., x, y, a.
Išraiškos – kombinacijos iš skaičių, kintamųjų ir veiksmų (pvz., 2x + 5). Išraiškos nėra lygios niekam kol jų neišsprendžiame ar nenurodome kintamojo reikšmės.
Lygtys – teiginiai, nurodantys, kad dvi išraiškos yra lygios (pvz., 3x + 1 = 10). Sprendžiant lygtį ieškoma tokių kintamųjų reikšmių, kurioms lygtys tampa teisingos.
Nelygybės – reiškia, kad vienas išreiškimas yra didesnis ar mažesnis už kitą (>, <, ≥, ≤). Jas sprendžiant taikomos panašios manipuliacijos kaip ir lygtyse, bet reikia atsižvelgti į ženklų taisykles (pvz., dalinant iš neigiamo skaičiaus sukeičiame nelygybės ženklą).
Funkcijos – taisyklės, susiejančios kiekvieną reikšmę iš vieno rinkinio su vienu (ar daugiau) reikšmių kitu rinkiniu. Dažnai rašomos kaip f(x) = ... . Jos padeda modeliuoti realius ryšius (pelnas, greitis–laikas ir kt.).
Savybės ir taisyklės – komutatyvumas (a + b = b + a), asociatyvumas ((a + b) + c = a + (b + c)), distributyvumas (a(b + c) = ab + ac) ir kt. Šios savybės padeda supaprastinti išraiškas ir spręsti lygtis.

Kaip spręsti paprastą lygti

Tipinis vieno nežinomo linearinės lygtys sprendimo planas:

1) Supaprastinti abi puses (sudėti panašius narius).
2) Atlikti operacijas, kad kintamasis liktų vienoje pusėje (atimti, pridėti, dalyti, dauginti).
3) Gaunant galutinę reikšmę patikrinti ją įstatant į pradinę lygti.

Pavyzdžiui, lygtyje 3x + 1 = 10 (kaip pavaizduota aukščiau) sprendimo žingsniai būtų:

Atimame 1 iš abiejų pusių: 3x = 9.
Daliname abi puses iš 3: x = 3.
Patikriname: 3·3 + 1 = 10 – teisinga.

Kiek sudėtingesni tipai ir metodai

Lygiagretūs skaičiavimai ir sistemų sprendimas – dviejų ar daugiau lygčių sistemos sprendžiamos pakeitimo, sudėjimo (eliminacijos) ar matricų (gaussinės eliminacijos) metodais.
Kvadratinės lygtys – turi formą ax^2 + bx + c = 0; sprendžiamos naudojant faktorizaciją, kvadratinę formulę arba paversiant kvadratu.
Išraiškų supaprastinimas – faktorizacija, trupmenų susilpninimas, laipsnių taisyklių taikymas.
Inequalities and intervals – darbo su nelygybėmis taisyklės, sprendinių aibės vaizdavimas ašyje.

Taikymai kasdienybėje ir profesijose

Elementarioji algebra naudojama daugelyje sričių:

Verslas ir ekonomika: sąnaudų–pajamų modeliai, pelno funkcijos, paskolų palūkanų skaičiavimas.
Mokslas ir inžinerija: fizikinių dydžių ryšiai, cheminės reakcijos tempai, optimizavimo uždaviniai.
Programavimas: algoritmų analizė, kintamųjų valdymas, loginių sąlygų vertinimas.
Kasdieniai sprendimai: biudžeto planavimas, receptų skalavimas, rūšiavimo ir matavimo problemos.

Patarimai mokantis elementariosios algebros

Pradėkite nuo aritmetikos pagrindų – geras skaičių jausmas labai padeda.
Aiškiai žymėkite kintamuosius ir rašykite žingsnius tvarkingai – taip lengviau rasti klaidas.
Praktikuokitės spręsdami daug pavyzdžių: lygtys, nelygybės, faktorizacija.
Nenaudokite skaičių vietoje kintamųjų visur – mokykitės paversti konkretų pavyzdį abstrakčia išraiška.
Jei įmanoma, pieškite grafikus – funkcijų grafikai padeda suprasti priklausomybes.

Ką mokytis toliau

Baigus elementariąją algebrą verta gilintis į:

Vidurinio lygio algebrą: kvadratinės lygtys, polinomai, racionalios išraiškos.
Analizę ir funkcijų teoriją: ribos, diferencialai ir integralai (vėlesnėse matematikos disciplinose).
Abstrakčiąją algebrą: grupės, žiedai, laukai – teorinė matematika, dažniausiai dėstoma aukštesnėse studijose.

Elementarioji algebra yra pagrindas, padedantis pereiti nuo skaičiavimo prie abstraktesnio mąstymo ir praktinių modelių kūrimo. Nuoseklus praktikos ir supratimo augimas leidžia lengviau įsisavinti sudėtingesnes matematikos sritis bei taikyti žinias realiame gyvenime.

Paprasti algebros uždaviniai

Jei lygtyje yra tik vienas nežinomas skaičius, kartais ją lengva išspręsti. Nežinomasis skaičius vadinamas "x":

2 x + 4 = 12. {\displaystyle 2x+4=12.\,} $2x+4=12.\,$

Norėdami išspręsti paprastą lygtį su vienu nežinomuoju, abi lygties puses pridėkite, atimkite, padauginkite arba padalykite iš to paties skaičiaus, kad nežinomasis x būtų vienoje lygties pusėje. Kai x bus vienoje pusėje, naudokite aritmetikos veiksmus, kad nustatytumėte, kokia suma yra kitoje lygties pusėje. Pavyzdžiui, atimdami 4 iš abiejų pirmiau pateiktos lygties pusių:

2 x + 4 - 4 = 12 - 4 {\displaystyle 2x+4-4=12-4\,} $2x+4-4=12-4\,$

gauti:

2 x = 8 {\displaystyle 2x=8\,} $2x=8\,$

Abi puses padalykite iš 2:

2 x 2 = 8 2 {\displaystyle {\frac {2x}{2}}={\frac {8}{2}}},} ${\frac {2x}{2}}={\frac {8}{2}}\,$

gauti:

x = 4. {\displaystyle x=4.\,} $x=4.\,$

Šią lygtį galima įsivaizduoti kaip sūpynes arba balansą: tai, ką darote vienoje pusėje, turite daryti ir kitoje, o pagrindinis jūsų tikslas - gauti x savaime.

Apibrėžtys

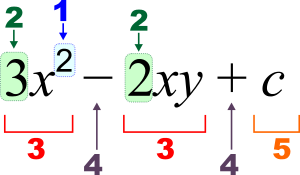
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c} $3x^{2}-2xy+c$ turi šias sudedamąsias dalis:

1 : eksponentas (galia), 2 : koeficientas, 3 : narys, 4 : operatorius, 5 : konstanta, x , y {\displaystyle x,y} : $x,y$ kintamieji

Klausimai ir atsakymai

K: Kas yra elementarioji algebra?

A: Elementarioji algebra - tai pati paprasčiausia algebros forma, kurios mokiniai mokomi. Ji paprastai seka po aritmetikos ir apima kintamųjų (pvz., a, x, y) naudojimą skaičiams lygtyse žymėti.

K: Kokie yra kai kurie elementariosios algebros panaudojimo būdai?

A: Elementarioji algebra gali būti naudojama sprendžiant nežinomų skaičių uždavinius, apibendrinant aritmetikos taisykles, suprantant ir kuriant funkcinius ryšius, taip pat dažnai naudojama daugelyje kitų dalykų, pavyzdžiui, moksle, versle ir statyboje.

K: Kaip elementarioji algebra padeda žmonėms suprasti abstrakčias idėjas?

A: Elementarioji algebra padeda žmonėms išmokti bendrųjų idėjų iš daugelio pavyzdžių, įrodant, kad a+b=b+a visiems a ir b. Tai leidžia geriau suprasti abstrakčias sąvokas.

K: Ar abstrakčioji algebra yra pažangesnė už elementariąją algebrą?

A: Taip, abstrakčioji algebra paprastai dėstoma vėlyvuoju koledžo etapu ir yra daug pažangesnė už elementariąją algebrą.

K: Kokių tipų lygtys sudaro elementariąją algebrą?

A: Elementarioji algebra apima lygtis su kintamaisiais (pvz., a, x, y), reiškiančiais skaičius, taip pat su operatoriais, tokiais kaip +, - , × ir ÷ .
3x+1=10 {\displaystyle 3x+1=10}

K: Kaip elementariosios algebros supratimas gali padėti mokytis kitų dalykų?

A: Elementariosios algebros supratimas gali padėti kituose dalykuose, pavyzdžiui, gamtos moksluose, versle ar statyboje, nes algebra leidžia spręsti nežinomų skaičių uždavinius ir kurti funkcinius ryšius tarp skirtingų kintamųjų.

Ieškoti