Jėgos momentas (momentas) — apibrėžimas, formulė ir pavyzdžiai
Jėgos momentas: aiškus apibrėžimas, formulė ir praktiniai pavyzdžiai — sužinokite, kaip momentas veikia svertus, duris, skriemulius ir inžinerinius sprendimus.
Fizikoje jėgos momentas (dažnai tiesiog momentas) yra jėgos gebėjimo sukelti kūno sukimąsi apie tam tikrą tašką arba ašį matas. Momentas apibūdina, kaip stipriai ir kuriame atstume nuo sukimosi ašies veikianti jėga duoda sukimo efektą.
Apibrėžimas ir paprasta formulė
Paprastai momentą apskaičiuojame kaip jėgos ir jai statmeno atstumo nuo sukimosi taško sandaugą:
Momentas = Jėga × statmenas atstumas {\displaystyle {\text{Momentas}}={\text{Jėgą}}\times {\text{Perpendikuliarų atstumą}}}
Šią formulę galima užrašyti taip: M = F · d⊥, kur F – jėga, o d⊥ – atstumas nuo sukimosi taško iki jėgos veikimo linijos (statmenas atstumas).
Vektorinė forma ir kampas
Vektoriškai momentas (talpinamas kaip sukimosi momentas arba torque) yra vektorinė sandauga:
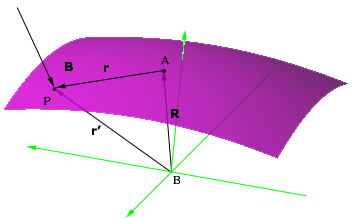
M = r × F,
kur r – vektorius nuo sukimo taško iki jėgos veikimo taško, F – jėgos vektorius. Momentas M turi kryptį, kurią nusako dešinės rankos taisyklė. Jo modulis lygus M = r F sinθ, kur θ – kampas tarp r ir F.
Ženklo konvencija ir pusiausvyra
Momentai gali būti laikomi teigiamais arba neigiamais priklausomai nuo pasirinktos konvencijos (dažniausiai teigiamas — sukimas prieš laikrodžio rodyklę). Bet kuriuo atveju pusiausvyros sąlyga sukantiems momentams yra:
- kai žiūrima pagal sukimosi kryptis: laikrodžio rodyklės (CW) momentų suma lygi prieš laikrodžio rodyklę (CCW) momentų sumai;
- algebrinė forma: ∑M = 0 (visų momentų algebraiška suma lygi nuliui).
Pora (momentas kaip poros efektas)
Jeigu dvi lygiagrečios, priešingos ir nesutampančios jėgos veikia poroje, jos sukuria vadinamąją porą (angl. couple). Poros momentas M = F · s, kur s – atstumas tarp jėgų veikimo linijų. Poros momentas sukelia tik sukimąsi (neturi poslinkio komponentės kūno centro atžvilgiu).
Vienetas ir atskyrimas nuo darbo/energijos
Momentų SI vienetas yra niutono metras (N·m). Taip pat galima išreikšti kaip kg·m²/s² (nes N = kg·m/s²). Svarbu pažymėti, kad nors matavimo vienetas N·m sutampa su J (džauliais) iš vienetinio požiūrio, momentas nėra darbas ar energija — tai skirtingos fizinės reikšmės.
Pavyzdžiai ir taikymas
Momentas pasireiškia daugelyje kasdienių ir inžinerinių situacijų. Keletas pavyzdžių:
- svirtis (svertai), pavyzdžiui, Svaras ar skriemulys ir krumpliaratis, kurios keičia momentinę rankeną ir taip suteikia mechaninį pranašumą;
- sūpuoklė — vaiko svyravimas priklauso nuo svorio ir atstumo nuo atramos;
- durų rankena ar vyriai — jėgos pritaikymas didesniame atstume palengvina atidarymą;
- veržliaraktis — ilgesnis raktas leidžia sukurti didesnį momentą pritaikius tą pačią jėgą;
- konservų atidarytuvai, laužtuvai, uždegimo rakteliai ir kt. paprastos mašinos, kurios veikdamos didina momentą ar pokyčius jame.
Praktiškas pavyzdys
Jeigu prie veržliaraktio, kurio rankena yra 0,20 m ilgio, pritaikome 50 N jėgą statmenai, momento dydis bus M = 50 N × 0,20 m = 10 N·m. Jeigu jėga nebūtų stataus kampo, naudotume M = rF sinθ.
Kiti susiję dalykai
Susijusios sąvokos: momento inercija (kiek masė priešinsis sukimui), sukimo greitis ir kampinis pagreitis (rotacinė dinamika) bei jėgos poros poveikis mechaninėse konstrukcijose. Momentų analizė yra pagrindinė mechanikos dalis konstravime, transporto priemonių, statybos ir daugelyje inžinerinių sričių.
Keletas pavyzdžių, kai taikomi momentai (sukimosi efektas), yra svertai, pavyzdžiui, sūpuoklės, atidaromos ir uždaromos durys, veržliarakčiai, konservų atidarytuvai ir laužtuvai.
Momento istorija
Momentų principas kildinamas iš Archimedo atrasto sverto veikimo principo. Svirte veikia jėga (jo laikais dažniausiai žmogaus raumenys), kuria veikiama ranka, tam tikra sija. Archimedas pastebėjo, kad objektą veikianti jėga, jėgos momentas, apibrėžiama kaip M = rF, kur F - veikianti jėga, o r - atstumas nuo veikiančios jėgos iki objekto.
Klausimai ir atsakymai
K: Kas yra galios momentas?
A: Jėgos momentas, dažnai vadinamas tiesiog sukamuoju momentu, yra jėgos tendencijos priversti objektą suktis apie tam tikrą tašką ar ašį matas.
K.: Kokį vaidmenį šioje koncepcijoje atlieka momentinė ranka?
Atsakymas: Momentinis petys yra atstumas nuo sukimosi ašies ir šioje koncepcijoje atlieka svarbų vaidmenį. Paprastos mašinos, pavyzdžiui, svertai, skriemuliai ir krumpliaračiai, sukuria mechaninį pranašumą keisdami sukimo momento rankeną.
K: Koks yra sukimo momento SI vienetas?
A: SI momentų matavimo vienetas yra niutono metras (kgm²/s²).
K: Kokia yra momentų skaičiavimo formulė?
Atsakymas: Momentų skaičiavimo formulė yra tokia: Momentas = jėga × statmenas atstumas.
Klausimas: Koks principas taikomas, kai svarstomi momentai?
Atsakymas: Momentų principas teigia, kad kai sistema yra pusiausvyroje, momentų pagal laikrodžio rodyklę suma turi būti lygi momentų prieš laikrodžio rodyklę sumai.
Klausimas: Kur yra pavyzdžių, kur taikomi momentai?
A: Momentų (atvirkštinio veikimo) taikymo pavyzdžiai - svirtys, pvz., svirtys, durų atidarymas ir uždarymas, veržliarakčiai, konservų atidarytuvai ir laužtuvai.
Klausimas: Kaip veikia svertai jėgų ir atstumų atžvilgiu?
A: Svaras veikia naudodamas vieną jėgą, vadinamą jėga, kad įveiktų kitą jėgą, vadinamą apkrova. Fizikoje momentas yra ir fizikinis dydis, ir atstumas.
Ieškoti
