Snelio lūžio dėsnis -
Snelio lūžio dėsnis - tai mokslinis šviesos ar kitų bangų lūžio dėsnis. Optikoje Snelio dėsnis susijęs su šviesos greičiu skirtingose terpėse. Šis dėsnis teigia, kad šviesai pereinant per skirtingas medžiagas (pavyzdžiui, iš oro į stiklą) kritimo (įėjimo) kampo ir lūžio (išėjimo) kampo sinusų santykis nesikeičia:
sin θ 1 sin θ 2 = v 1 v 2 = n 2 n 1 {\displaystyle {\frac {\sin \theta _{1}}}{\sin \theta _{2}}}={\frac {v_{1}}{v_{2}}}={\frac {n_{2}}{n_{1}}}} 
Kiekviena θ {\displaystyle \theta }
yra kampas, matuojamas nuo ribos normalės, v {\displaystyle v}
- šviesos greitis atitinkamoje terpėje (SI vienetai yra metrai per sekundę arba m/s). n {\displaystyle n}
- terpės lūžio rodiklis.
Vakuumo lūžio rodiklis yra 1, o šviesos greitis vakuume yra c {\displaystyle c}
. Kai banga praeina pro medžiagą, kurios lūžio rodiklis yra n, bangos greitis tampa c n {\displaystyle {\frac {c}{n}}}. 
.
Snello dėsnį galima įrodyti Fermato principu. Fermato principas teigia, kad šviesa sklinda tuo keliu, kuris užima mažiausiai laiko.
Šviesos spindulys patenka į stiklinę prizmę ir lūžta
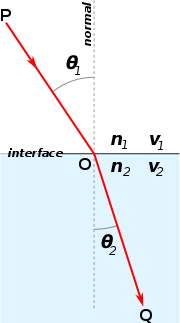
Šviesos lūžis dviejų skirtingų lūžio rodiklių terpių, kurių n2 > n1, sandūroje
Istorija
Ši idėja turi ilgą istoriją. Šia problema domėjosi Aleksandrijos Herojus, Ptolemėjas, Ibn Sahlas ir Hiūgenas. Ibn Sahlas iš tikrųjų atrado lūžio dėsnį. 1678 m. knygoje Traité de la Lumiere Huygensas parodė, kaip Snello sinusoidės dėsnį galima paaiškinti arba išvesti iš banginės šviesos prigimties.
Klausimai ir atsakymai
K: Kas yra Snelio lūžio dėsnis?
A: Snelio lūžio dėsnis yra mokslinis šviesos ar kitų bangų lūžio dėsnis. Optikoje jis teigia, kad šviesai pereinant pro skirtingas medžiagas, kritimo ir lūžio kampų sinusų santykis nesikeičia.
K: Kaip galima įrodyti Snelio dėsnį?
A: Snelio dėsnį galima įrodyti remiantis Fermos principu, kuris teigia, kad šviesa sklinda tuo keliu, kuris užima mažiausiai laiko.
K: Kas yra Fermato principas?
A: Fermato principas teigia, kad šviesa sklinda keliu, kuris užima mažiausiai laiko.
K: Kas yra n ir v Snelio dėsnyje?
Atsakymas: n yra terpės lūžio rodiklis, o v - šviesos greitis toje terpėje (matuojamas metrais per sekundę).
K: Ką reiškia c Snelio dėsnyje?
A: c reiškia šviesos greitį vakuume, kurio lūžio rodiklis lygus 1.
K: Kaip apskaičiuoti greitį, kai banga sklinda per medžiagą, kurios lūžio rodiklis n?
A: Kai banga sklinda per medžiagą, kurios lūžio rodiklis n, greitis tampa c/n.
