Gauso Egregium teorema — paviršiaus kreivumo nepriklausomumas
Gauso Egregium teorema: kaip paviršiaus kreivumas išlieka nepakitęs be įterpimo — supraskite fundamentalią diferencialinės geometrijos paslaptį.
Gauso Egregium teorema (lot. Theorema Egregium) – svarbus diferencialinės geometrijos rezultatas, kurį įrodė Karlas Frydrichas Gausas (Carl Friedrich Gauss). Teorema susijusi su paviršių kreivumu ir teigia, kad tam tikras kreivumo matas — Gauso kreivumas — yra intrinziškas, t. y. jį galima nustatyti vien matuojant kampus, atstumus ir jų pokyčius paviršiuje, nepriklausomai nuo to, kaip tas paviršius yra įterptas į jį supančią trimatę Euklidinę erdvę. Kitaip tariant, paviršiaus Gauso kreivumas nepasikeičia, jei paviršių lenkiame ar sukiame jo netempdami (paliekant vietinį atstumų tarp taškų nepakitusį).
Apibrėžimas ir reikšmė
Gauso kreivumas K taške paprastai išreiškiamas per du pagrindinius kreivumo dydžius — principalinius kreivumus k1 ir k2 — kaip jų sandauga: K = k1 · k2. Pirmai apibrėžčiai buvo svarbu, kaip paviršius guli erdvėje, nes principaliniai kreivumai gaunami iš paviršiaus antrinės fundamentinės formos. Tačiau Gauso Egregium teorema parodo, kad galutinė išraiška K gali būti išreikšta vien per pirmąją fundamentinę formą (metrikinę struktūrą) ir jos pirmųjų bei antrųjų išvestinių komponentes — tai reiškia, kad K priklauso tik nuo paviršiaus metrikos ir jos išvestinių, t. y. nuo intrinziškų duomenų.
Gauso įrodymo idėja ir pasekmės
- Idėja: Gausas parodė, jog Tam tikri išraiškų deriniai, susiję su antrine fundamentine forma, gali būti perrašyti tik per metrines charakteristikas. Kitaip tariant, kreivumo formulė gali būti sukurta taip, kad matyti — K priklauso tik nuo metrikos ir jos išvesčių, o ne nuo išorinio įterpimo.
- Pasekmė: jei du paviršiai yra lokaliai izometriniai (t. y. susieti vietine ilgio ir kampų išsaugojančia žemėlapio transformacija), jie turi tą patį Gauso kreivumą kiekviename atitinkamame taške. Tai reiškia, jog neįmanoma ištempti ir išlyginti sferos į plokštumą be tempimo ar deformacijų, nes sfera turi teigiamą kreivumą, o plokštuma — nulį.
- Praktinis pavyzdys: cilindras yra lokaliai izometriškas plokštumai (galima „apvynioti“ plokštumą į cilindrą be tempimo), todėl cilindro Gauso kreivumas yra lygus nuliui — toks pat kaip plokštumos. Tai paaiškina, kodėl galima atkirpti popieriaus juostą ir nusiųsti ją ant tūbinio vamzdžio be klastočių.
Pavyzdžiai
- Plokštuma: K = 0.
- Sfera radius R: K = 1/R² (teigiamas kreivumas), todėl sferos vietinės geometrijos negalima atvaizduoti plokštumoje be iškraipymų.
- Cilindras: nors jis vizualiai „išlinkęs“ erdvėje, lokaliai jis yra izometriškas plokštumai, todėl K = 0.
Istorinis ir platesnis reikšmės kontekstas
Gausas savo darbą aprašė veikalė "Disquisitiones generales circa superficies curvas" (1827). Teorema buvo vadinama „egregium“ (išskirtine, nuostabia) todėl, kad ji suteikė netikėtą rezultatą: nors kreivumo pradinis apibrėžimas atrodė priklausantis nuo išorinės padėties erdvėje, galutinis kreivumo matas iš tikrųjų yra intrinziškas. Tai turėjo didelę įtaką vėlesnei diferencialinės geometrijos plėtrai ir supratimui apie metrikas, kurias galima apibūdinti be nuorodų į išorinę erdvę.
Ryšiai su modernia matematika ir fizika
Gauso Egregium teorema yra viena iš fundamentalių idėjų, vedančių prie platesnių koncepcijų, kaip Riemanno geometrija, kuri nagrinėja kreivumą ir metrines savybes aukštesnės dimensijos erdvėse. Taip pat jos idėjos yra svarbios fizikoje — pavyzdžiui, bendrojoje reliatyvumo teorijoje erdvė-laikas aprašomas intrinziškais geometriniais dydžiais (krivumo tensoriais), nepriklausomai nuo to, kaip tą erdvę įsivaizduojame įterptą į kokią nors aukštesnę foninę erdvę.
Dėl šios priežasties ankstesniame straipsnyje pateikta formulė pati savaime veda prie nuostabios teoremos. Jei kreivas paviršius išvystomas ant bet kokio kito paviršiaus, kreivumo matas kiekviename taške išlieka nepakitęs.
Apibendrinant: Gauso Egregium rodo, kad Gauso kreivumas yra intrinziška paviršiaus savybė — ją galima nustatyti vien remiantis paviršiaus metrika, todėl lenkimas be tempimo neiškreipia šio kreivumo.
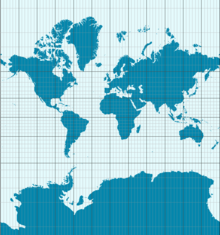
Egregijaus teorijos pasekmė yra ta, kad Žemė negali būti vaizduojama žemėlapyje be iškraipymų. Čia parodyta Merkatoriaus projekcija išsaugo kampus, bet pakeičia plotą. Pavyzdžiui, Antarktida vaizduojama daug didesnė nei yra iš tikrųjų.
Klausimai ir atsakymai
K: Kas yra Gauso "Theorema Egregium"?
A: Gauso Egregium teorema yra pagrindinis diferencialinės geometrijos rezultatas apie paviršių kreivumą, kurį įrodė Karlas Frydrichas Gausas (Carl Friedrich Gauss).
K: Kaip, remiantis Gauso Egregium teorema, galima nustatyti kreivumą?
A: Pagal Gauso Egregium teoremą kreivumą galima nustatyti matuojant tik kampus, atstumus ir jų santykius paviršiuje.
Klausimas: Ar norint nustatyti kreivumą reikia kalbėti apie tai, kaip konkrečiai paviršius įterptas į jį supančią trimatę Euklidinę erdvę?
Atsakymas: Ne, norint nustatyti kreivumą pagal Gauso "Theorema Egregium", nebūtina kalbėti apie tai, kokiu konkrečiu būdu paviršius įterptas į jį supančią trimatę Euklidinę erdvę.
Klausimas: Ar pasikeičia paviršiaus Gauso kreivumas, jei paviršių lenkiame jo netempdami?
Atsakymas: Ne, paviršiaus Gauso kreivumas nesikeičia, jei paviršių lenkiame jo netempdami pagal Gauso Egregium teoremą.
K: Kas taip pateikė šią teoremą?
Atsakymas: Taip teoremą pateikė Gausas.
K: Kuo ši teorema yra žymi?
Atsakymas: Teorema yra "žymi", nes pradiniame Gauso kreivumo apibrėžime tiesiogiai naudojama paviršiaus padėtis erdvėje. Todėl gana netikėta, kad rezultatas nepriklauso nuo jo įterpimo, nepaisant visų patiriamų lenkimo ir sukimo deformacijų.
Klausimas: Kokiu būdu Gausas pateikė teoremą?
Atsakymas: Gausas teoremą pateikė taip, kad jei kreivas paviršius išvystomas bet kuriame kitame paviršiuje, kreivumo matas kiekviename taške išlieka nepakitęs.
Ieškoti