Youngo-Laplace'o lygtis
Fizikoje Youngo-Laplace'o lygtis (/ləˈplɑːs/) yra netiesinė dalinė diferencialinė lygtis, kuri aprašo kapiliarinio slėgio skirtumą dviejų statinių skysčių, pavyzdžiui, vandens ir oro, sąsajoje. Šį skirtumą lemia paviršiaus įtempimo arba sienelės įtempimo reiškinys. Sienelės įtempimą galima taikyti tik labai plonoms sienelėms. Youngo-Laplace'o lygtis sieja slėgių skirtumą su paviršiaus arba sienelės forma. Ji labai svarbi tiriant statinius kapiliarinius paviršius.
Fiziologijoje jis vadinamas Laplaso dėsniu. Jis naudojamas slėgiui tuščiaviduriuose organuose apibūdinti.
Lygtis pavadinta Thomo Youngo, kuris 1805 m. sukūrė kokybinę paviršiaus įtempimo teoriją, ir Pierre'o-Simono Laplace'o, kuris kitais metais užbaigė matematinį aprašymą, vardu. Kartais ji dar vadinama Youngo-Laplace'o-Gauso lygtimi: 1830 m. Karlas Frydrichas Gausas (Carl Friedrich Gauss) suvienodino Youngo ir Laplace'o darbus. Gaussas diferencialinę lygtį ir ribines sąlygas nustatė naudodamasis Johanno Bernoulli virtualaus darbo principais.
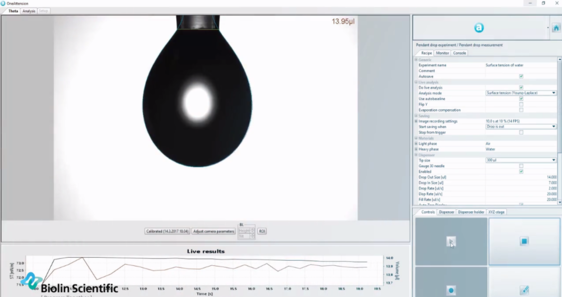
Optiniai tenziometrai naudoja Youngo-Laplace'o lygtį, kad automatiškai nustatytų skysčio paviršiaus įtempimą pagal pakabuko lašelio formą.
Klausimai ir atsakymai
K: Kas yra Youngo-Laplace'o lygtis?
A: Joungo-Laplaso lygtis yra netiesinė dalinė diferencialinė lygtis, kuri aprašo kapiliarinio slėgio skirtumą dviejų statinių skysčių, pavyzdžiui, vandens ir oro, sąsajoje.
K: Su kuo ji susijusi?
A: Ji susijusi su slėgio skirtumu ir paviršiaus arba sienelės forma.
K: Kas sukūrė šią teoriją?
A: 1805 m. teoriją sukūrė Thomas Youngas, o kitais metais Pierre'as-Simonas Laplace'as užbaigė jos matematinį aprašymą. Vėliau, 1830 m., ją suvienodino Carlas Friedrichas Gaussas.
K: Kaip ji naudojama fiziologijoje?
A: Fiziologijoje šis dėsnis vadinamas Laplaso dėsniu ir naudojamas slėgiui tuščiaviduriuose organuose apibūdinti.
K: Kokį reiškinį jis paaiškina?
A.: Youngo ir Laplace'o lygtis paaiškina paviršiaus arba sienelių įtempimo reiškinį.
Klausimas: Ar sienelės įtempimas taikomas storoms sienelėms? Atsakymas: Ne, sienelių įtempimą galima taikyti tik labai plonoms sienelėms.
