Elipsė: geometrijos apibrėžimas, židiniai, lygtis ir pavyzdžiai
Elipsė – tai uždara simetriška plokštumos kreivė, primenanti ovalą arba suplotą apskritimą. Geometriškai elipsė gali būti apibrėžiama keliais ekvivalentiniais būdais:
Apibrėžimai
- Kaip kūgio pjūvis: elipsė atsiranda, kai kūgiui susikirtus su plokštuma gaunama uždara kreivė (ne apskritimas). Geometrijoje tai yra viena iš pagrindinių konikinių sekcijų.
- Kaip vieta: elipsė yra visų plokštumos taškų rinkinys, kurių atstumų iki dviejų fiksuotų taškų (vadinamų židiniais) suma yra konstanta. Kitaip tariant, visi taškai P = (x,y) tenkina d(P,F1) + d(P,F2) = 2a, kur 2a yra pastovus didžiausios ašies ilgis.
Standartinė lygtis
Jei elipsės centras yra taške (h,k) ir elipsės pusiau ašys yra a bei b, tai elipsės standartinė lygtis parašoma kaip
(x-h)²/a² + (y-k)²/b² = 1
Jeigu a ≥ b, tai pusiau didžioji ašis yra ilgumo a ir viso didžiausios ašies ilgis yra 2a; trumpesnė pusiau ašis yra b (viso 2b). Jeigu a < b, pažymėjimą galima apsikeisti – didžioji ašis bus vertikali.
Savybės ir elementai
- Centras: (h,k).
- Viršūnės (vertices): jeigu didžioji ašis horizontalioji (a ≥ b), viršūvės yra (h±a, k); jei vertikali – (h, k±a).
- Židiniai (foci): židinių koordinatės priklauso nuo orientacijos. Jei didžioji ašis horizontalioji, židiniai yra (h±c, k); jei vertikali – (h, k±c). Čia c yra atstumas nuo centro iki kiekvieno židinio.
- Santykis tarp a, b ir c: c² = a² − b² (prisiminkite: c yra atstumas nuo centro iki židinio, ne tarp židinių).
- Ekscentriškumas: e = c/a. Jis apibrėžia, kiek elipsė yra „ištempusi“; 0 ≤ e < 1. Jeigu a = b, tuomet e = 0 ir elipsė tampa apskritimu.
Parametrinė forma ir tiesioginis konstravimas
Parametrinė elipsės pateikimo forma su centru (h,k):
x = h + a cos t, y = k + b sin t, kur t ∈ [0,2π).
Praktinis braižymo būdas: įkišus du smeigtukus (židinius) į kartoną ir aplink juos apjuosus virvelę, į kilpą įkišus pieštuką ir traukus virvelę, pieštukas braižys elipsę – tai atitinka apibrėžimą per atstumų sumą.
Plotas ir perimetras
Plotas: S = πab.
Perimetras: neturi paprasto elementaraus uždaro formos išraiškos. Yra daug aproksimacijų; viena tikslesnių Ramanujan formulių:
P ≈ π [3(a + b) − sqrt{(3a + b)(a + 3b)}].
Pavyzdys
Tarkime elipsė centro (0,0) su a = 5 ir b = 3. Jos lygtis:
x²/25 + y²/9 = 1.
Skaičiavimai: c = sqrt(5² − 3²) = sqrt(25 − 9) = 4, todėl židiniai yra (±4, 0). Ekscentriškumas e = c/a = 4/5 = 0.8. Plotas S = π·5·3 = 15π. Viršūvės: (±5,0) ir (0,±3).
Taikymas
Elipsės dažnai pasitaiko gamtoje ir technologijose: planetų orbitos aplink Saulę (pagal Keplerio dėsnius) yra elipsės, kurių viename židinyje yra Saulė; optikoje elipsinės formos turi savybių, kad spinduliai, išeinantys iš vieno židinio, atsispindi į kitą židinį; inžinerijoje elipsės naudojamos laiptų, laukų, reflektorių, akustinių konstrukcijų projektuose.
Papildomi pastabos
- Apskritimas yra specialus elipsės atvejis, kai a = b.
- Elipsės lygties orientacija gali būti pasvirusi; tuomet reikia naudoti bendrą kvadratinę formą su xy termu arba taikyti sukimo koordinatų transformacijas.
- Directrix (tiesės) lygtis elipsei: atstumas iki židinio / atstumas iki directrix = e. Directrix koordinatės priklauso nuo orientacijos ir e.
Elipsė, gaunama kaip kūgio ir plokštumos susikirtimas.
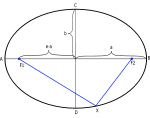
Elipsė ir jos savybės.
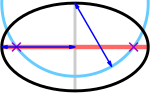
Židiniai (violetiniai kryželiai) yra pagrindinės ašies (raudona) ir apskritimo (žydra), kurio spindulys lygus pusiau didžiajai ašiai (mėlyna), susikirtimo taškuose, kurių centras yra mažosios ašies (pilka) gale.
Klausimai ir atsakymai
K: Kas yra elipsė?
A: Elipsė - tai figūra, kuri atrodo kaip ovalas arba suplotas apskritimas. Geometrijoje tai plokštumos kreivė, kuri atsiranda kūgiui susikirtus su plokštuma taip, kad gaunama uždara kreivė.
K: Kaip sukurti elipsę?
Atsakymas: Elipsę galima sukurti į kartoninę dėžutę įsmeigus du smeigtukus, tada aplink tuos du smeigtukus apvyniojus virvelę, į kilpą įkišus pieštuką ir tempiant į visas puses, kiek įmanoma nenutraukiant virvelės.
K: Kas yra apskritimai?
A: Apskritimai yra specialūs elipsių atvejai, kai pjovimo plokštuma yra statmena kūgio ašiai.
K: Kiek židinių turi elipsė?
A: Elipsė turi du židinius.
K: Kokia lygtis apibūdina elipsę?
A: Elipsės lygtis yra (x - h)²/a² + (y - k)²/b² = 1, kur h ir k žymi elipsės centrą, 2a - ilgį nuo abiejų ilgesnės kraštinės galų, o 2b - ilgį tarp abiejų trumpesnės kraštinės galų. C reiškia ilgį tarp jos židinio ir centro, todėl A²-B²=C².
Klausimas: Kur matome elipsinių orbitų pavyzdžių?
A: Elipsines orbitas galima pamatyti planetose, kurių viename židinyje yra Saulė.
