Eulerio-Bernoulli sijų teorija: apibrėžimas, principai ir taikymai
Sužinokite Eulerio–Bernoulli sijų teorijos apibrėžimą, pagrindinius principus ir praktinius taikymus inžinerijoje — aiškiai, koncentruotai ir pritaikoma.
Eulerio-Bernoulli sijų teorija (dar vadinama inžinierių sijų teorija arba klasikine sijų teorija) - tai paprastas metodas sijų lenkimui, kai veikia apkrova, apskaičiuoti. Jis taikomas mažoms sijos deformacijoms (kiek kas nors pasislenka), neatsižvelgiant į šlyties deformacijų poveikį. Todėl ją galima laikyti specialiuoju Timošenko sijų teorijos atveju. Ji pirmą kartą buvo pristatyta apie 1750 m. Ji išpopuliarėjo XIX a. pabaigoje kuriant Eifelio bokštą ir Velnio ratą. Vėliau ji buvo naudojama daugelyje inžinerijos sričių, įskaitant mechanikos inžineriją ir civilinę inžineriją. Nors buvo sukurti kiti pažangūs metodai, Eulerio-Bernoulli sijų teorija vis dar plačiai naudojama dėl savo paprastumo.
Pagrindinės prielaidos
- Plokštės išlikimas plokštėmis: skerspjūvio plokštės, kurios prieš lenkimą buvo plokščios, lieka plokštės po lenkimo (nereikšmingas skerspjūvio deformavimasis).
- Neutralioji ašis: skerspjūvio taškai, esantys neutraliojoje ašyje, nekeičia ilgio — jie nėra tempiami ar suspaudžiami dėl lenkimo.
- Mažos deformacijos ir linijinė elastingumo prielaida: kampų poslinkiai ir nuotoliai yra pakankamai maži, kad taikytųs linijinės elastinės ryšys tarp momento ir kreivumo.
- Šlyties deformacijos yra nepaisomos: tangentinės jėgos neatneša reikšmingos papildomos nuokrypos, todėl teorija tinka plonoms, santykinai ilgioms sijoms (ilgis daug didesnis už aukštį).
Esminės formulės ir lygtis
Pagrindinė diferencialinė lygtis statinėms apkrovoms vienmatėje sijos lenkimo analizei:
EI · d4w/dx4 = q(x),
čia E – medžiagos Youngo modulis, I – skerspjūvio inercijos momentas, w(x) – skersinis nuokrypis, q(x) – išorinė paskirstytoji apkrova (jėga vienetui ilgio). Iš jos per integravimą gaunami lenkimo momentai, posvyriai ir poslinkiai, taikant tinkamas ribines sąlygas.
Ryšys tarp lenkimo momento ir kreivumo:
M(x) = −EI · d2w/dx2 (ženkai priklausomai nuo konvencijų),
kur M(x) yra lenkimo momentas, o d2w/dx2 – sijos kreivumo apytikslis dydis (mažų poslinkių prielaida).
Bendrų ribinių sąlygų pavyzdžiai
- Stacionarus ir laisvas galas (kantis): w = 0, dw/dx = 0 (jei užfiksuotas); laisvas galas: M = 0, Q = 0.
- Atrama su ramsčiu (simply supported): w = 0, M = 0 (kreivumo sąlyga gali skirtis pagal konvenciją).
- Užfiksuotas galas (įkalintas): w = 0 ir dw/dx = 0.
Praktiniai formulės pavyzdžiai
- Kantis sijos galas, galutinis koncentrinis jėgos P poveikis: maksimalus galinis nuokrypis w_max = P L^3 / (3 E I).
- Kantinero sija su tolygiai paskirstyta apkrova q0: galinis poslinkis ties laisvu galu w_max = q0 L^4 / (8 E I).
- Pastaba: tikslūs skaitmeniniai koeficientai priklauso nuo ribinių sąlygų ir apkrovos tipo; sudėtingesniems atvejams sprendimas gaunamas integruojant pagrindinę dif. lygtį arba taikant metodus, pvz., superpoziciją ar formulus iš lentelių.
Stabilumas (Eulerio kolapsas)
Eulerio-Bernoulli teorija taip pat naudojama stulpų (ašinių elementų) kritiniam sprogimui (buckling) apskaičiuoti. Bazinis Eulerio kritinės apkrovos formulės pavidalas:
P_cr = π^2 E I / L_eff^2,
čia L_eff – efektyvus ilgis, atsižvelgiant į ribines sąlygas (dažnai rašomas kaip L_eff = K · L, kur K – efektyvumo faktorius: pavyzdžiui, K = 1 (atrama–atrama), K ≈ 0.7 (užfiksuota–atrama), K = 0.5 (užfiksuota–užfiksuota), K = 2 (kantis)).
Taikymo sritys
- Statyba: lentynos, sijos, tilto elementai.
- Mechanikos inžinerija: rėmai, kranų sijos, velenai, sparnų konstrukcijos.
- Mašinų dalys: ašys, sijos, rėmai, kur deformacijos mažos ir geometrija santykinai plona.
- Švietimas ir greitieji preliminarūs projektavimo skaičiavimai dėl formulės paprastumo.
Apribojimai ir alternatyvos
- Eulerio-Bernoulli teorija netinkama trumpoms arba storoms sijoms, kuriose šlytis (shear) duoda reikšmingą indėlį — tokiems atvejams naudojama Timoshenko sijų teorija.
- Dinaminiai atvejai su dideliu šlyties poveikiu ar sukiniais inercijos efektais reikalauja papildomų korekcijų (rotacinė inercija, šlyties deformacijos).
- Plastinės deformacijos, medžiagų nelinijiškumas, arba dideli poslinkiai reikalauja ne linijinių modelių arba skaitinių metodų (pvz., baigtinių elementų metodas).
Pastabos praktikai
Eulerio-Bernoulli teorija suteikia aiškų ir greitą būdą įvertinti sijos elgseną ir dažnai yra pakankama pradiniam projektavimui. Didesniems sudėtingumams arba kai ribinės sąlygos, skerspjūvio geometrija ar medžiagos savybės yra nestandartinės, rekomenduojama naudoti skaitinius metodus (FEM) arba pažiūrėti į pažangesnes teorijas (Timoshenko, neelastinės analizės).
Trumpai: Eulerio-Bernoulli teorija – paprasta, intuityvi ir efektyvi priemonė sijos lenkimui analizuoti, kuri, žinant jos prielaidas ir ribotumus, išlieka plačiai taikoma inžinerinėje praktikoje.
Vibruojanti stiklinė sija, rodanti sijų lenkimą, kurį galima įvertinti taikant Eulerio-Bernoulli sijų teoriją.
Istorija
Leonhardas Euleris ir Danielis Bernoulli 1750 m. pirmieji sukūrė šią teoriją. Tuo metu į mokslą ir inžineriją buvo žiūrima kitaip nei šiandien. Tokiomis matematinėmis teorijomis, kaip Eulerio ir Bernulio spindulių teorija, nebuvo pasitikima praktiniam inžineriniam naudojimui. Tiltai ir pastatai buvo projektuojami tais pačiais metodais iki pat XIX a. pabaigos. Tuomet Eifelio bokštas ir Velnio ratas parodė teorijos pagrįstumą platesniu mastu.
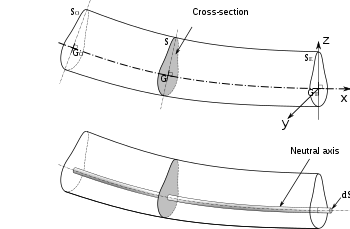
Lenkiamos sijos skerspjūvio brėžinys, kuriame pavaizduota neutralioji ašis
Statinė sijos lygtis
Toliau pateikta Eulerio-Bernoulli lygtis apibūdina ryšį tarp sijos deformacijos ir veikiančios apkrovos:
d 2 d x 2 ( E I d 2 w d x 2 ) = q {\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}}} kairė(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}}} dešinė)=q\,} 
Kur w ( x ) {\displaystyle w(x)} 
apibūdina sijos įlinkį z {\displaystyle z}
kryptimi tam tikroje padėtyje x {\displaystyle x}
. q {\displaystyle q}
yra paskirstytoji apkrova, kitaip tariant, jėga, tenkanti ilgio vienetui (analogiškai slėgiui, kuris yra jėga, tenkanti plotui); ji gali būti x {\displaystyle x} , w {\displaystyle w} funkcija. 
arba kiti kintamieji.
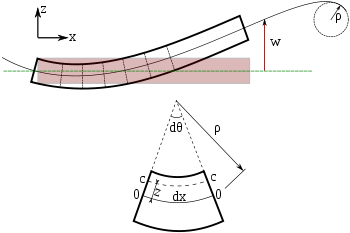
Eulerio-Bernoulli sijos lenkimas. Kiekvienas sijos skerspjūvis yra 90 laipsnių kampu neutralios ašies atžvilgiu.
Klausimai ir atsakymai
Klausimas: Kas yra Eulerio-Bernoulio spindulių teorija?
A: Eulerio-Bernoulli sijų teorija yra paprastas metodas, naudojamas sijų lenkimui skaičiuoti veikiant apkrovai, neatsižvelgiant į šlyties deformacijų poveikį.
K: Kada pirmą kartą buvo pradėta taikyti Eulerio-Bernoulli sijų teorija?
A: Eulerio-Bernoulli sijų teorija pirmą kartą buvo pradėta taikyti apie 1750 m.
K: Ar Eulerio-Bernoulli sijų teorija buvo naudojama kuriant Eifelio bokštą ir Velnio ratą?
A: Taip, Eulerio-Bernoulli sijų teorija išpopuliarėjo XIX a. pabaigoje kuriant Eifelio bokštą ir Velnio ratą.
K: Kokiose inžinerijos srityse buvo naudojama Eulerio-Bernoulli sijų teorija?
A.: Eulerio-Bernoulli sijų teorija buvo naudojama daugelyje inžinerijos sričių, įskaitant mechanikos inžineriją ir civilinę inžineriją.
K: Ar Eulerio-Bernoulli sijų teorija vis dar plačiai naudojama šiandien?
A: Taip, Eulerio-Bernoulli sijos teorija dėl savo paprastumo vis dar plačiai naudojama, nors buvo sukurti ir kiti pažangūs metodai.
K: Kokių tipų sijos įlinkiams taikoma Eulerio-Bernoulli sijos teorija?
A: Eulerio-Bernoulli sijos teorija taikoma mažiems sijos įlinkiams.
K: Ar Eulerio-Bernoulli sijos teorijoje atsižvelgiama į šlyties deformacijų poveikį?
Atsakymas: Ne, Eulerio-Bernoulli sijos teorija neatsižvelgia į šlyties deformacijų poveikį.
Ieškoti