Tiesinė regresija — apibrėžimas, mažiausiųjų kvadratų metodas ir taikymai
Tiesinė regresija: aiškus apibrėžimas, mažiausiųjų kvadratų metodas ir praktiniai taikymai — prognozavimas, kintamųjų įvertinimas ir modelių pritaikymas.
Tiesinė regresija – tai metodas, leidžiantis apibūdinti ryšį tarp priklausomo kintamojo ir vieno arba daugiau aiškinamųjų kintamųjų naudojant tiesę (arba tiesinį modelį). Tai specifinis regresinės analizės atvejis, kai modelis yra tiesinis pagal nežinomus parametrus.
Kas yra tiesinis modelis ir kodėl jis svarbus
Tiesinė regresija buvo vienas pirmųjų ir plačiausiai ištirtų regresinės analizės tipų. Modeliai, kurie yra tiesiniai pagal parametrus, yra paprastesni pritaikyti ir analitiškai išnagrinėti nei netiesiniai modeliai. Dėl to lengviau gauti parametrų įverčius, apskaičiuoti jų sklaidos matmenis ir atlikti statistinę išvadą apie ryšį tarp kintamųjų.
Pagrindinės taikymo sritys
- Tiesinė regresija dažnai naudojama kurti prognozavimo modeliams iš stebimų verčių rinkinių. Sukūrus modelį, jam pateikus naują X reikšmę (kai nežinoma y), pagal pritaikytą modelį galima prognozuoti y reikšmę.
- Jei turime priklausomą kintamąjį y ir keletą aiškinamųjų X1, ..., Xp, tiesinė regresija padeda kiekybiškai įvertinti ryšio tarp y ir kiekvieno Xj stiprumą, nustatyti, kurie Xj reikšmingai siejasi su y, bei identifikuoti perteklinės informacijos ar priklausomybės poaibius tarp aiškinamųjų kintamųjų.
Mažiausiųjų kvadratų (MK) metodas
Dažniausiai taikomas metodas tiesinei regresijai pritaikyti yra mažiausiųjų kvadratų (MK) metodas. Jis remiasi prielaida, kad geriausias modelis yra tas, kuriame suma kvadratų išlikimų (residualų) yra mažiausia. Tai reiškia, kad ieškoma parametrų aibės, minimizuojančios ∑(y_i − ŷ_i)^2, kur ŷ_i – modelio prognozė.
Multi-dimensinėje formoje MK sprendinys dažnai išreiškiamas matriciniu formatu: β̂ = (XᵀX)⁻¹ Xᵀ y, kur X – aiškinamųjų kintamųjų matrica, y – priklausomų kintamųjų vektorius, o β̂ – parametrų įvertis. Ši formulė galioja, kai XᵀX yra invertuojama.
Svarbu pabrėžti, kad nors MK dažnai siejamas su tiesiniais modeliais, mažiausiųjų kvadratų metodas gali būti taikomas ir netiesiniams modeliams (kai modelis netiesinis pagal kintamuosius, bet tiesinis pagal parametrus arba kai naudojamos skaitinės optimizacijos metodikos).
Statistinės prielaidos ir savybės
- Lineariškumas pagal parametrus: modelis yra tiesinis pagal parametrus arba gali būti pavaizduotas tokiu pavidalu.
- Nepriklausomos, vidurkis lygus nuliui: liekanos turi nulio vidurkį ir yra nepriklausomos (arba bent nepriklauso nuo aiškinamųjų kintamųjų).
- Homoskedastiškumas: liekanų dispersija yra pastovi visiems stebiniams (jei ši prielaida laužoma — yra heteroskedastiškumas).
- Neautokoreliacija: liekanos nėra susijusios laiko ar vietos sekoje (svarbu laiko eilutėms).
- Gauss–Markovo teorema: esant pirmosioms keturioms prielaidoms (be prielaidos apie normalumą), MK įverčiai yra geriausi tarp lygiaverčių (BLUE — Best Linear Unbiased Estimator) — t. y. turi mažiausią dispersiją tarp visų linarių, nešališkų įverčių.
- Normalumas: jei liekanos yra normalios, parametrai turi paprastą parametrinę inferenciją (t-testai, F-testai, konfidencijos intervalai).
Vertinimas ir diagnostika
- R² ir pakoreguotas R²: matuoja, kokią dalį priklausomo kintamojo dispersijos paaiškina modelis. Pakoreguotas R² kompensuoja už kintamųjų skaičių.
- T-testai ir F-testai: naudojami atskiram parametrui arba visų parametrų reikšmingumui įvertinti.
- Liekanų analizė: liekanų grafikai, QQ-plotai, Breusch–Pagan testas (heteroskedastiškumui), Durbin–Watson testas (autokoreliacijai) ir kt.
- Multikolineritytė: jei du ar daugiau aiškinamųjų kintamųjų yra stipriai susiję tarpusavyje, MK įverčiai gali būti nestabilūs; tai tikrinama pagal VIF (variance inflation factor) ir kt.
Reguliarizacija ir alternatyvos
Kai kintamųjų daug arba egzistuoja multikolineritytė, taikomos reguliarizacijos metodikos, pvz. ridge regresija (L2 bauda) arba lasso (L1 bauda), kurios mažina parametrų dispersiją ir gali atlikti kintamųjų atranką. Taip pat egzistuoja robustinės metodikos (pvz., mažiausiųjų absoliutinių nuokrypių regresija), kvantilinė regresija, GLM (generalizuotieji tiesiniai modeliai) ir netiesiniai regresijos metodai.
Praktiniai taikymai ir pavyzdžiai
Tiesinė regresija plačiai taikoma ekonomikoje (pvz., pajamų prognozavimas), finansuose (rizikos modeliavimas), inžinerijoje (matavimo modeliai), medicinoje (veiksnių poveikis ligos rizikai), marketinge (pardavimų prognozės) ir daugelyje kitų sričių. Svarbu prisiminti: geras regresijos modelis reikalauja ne tik statistinio pritaikymo, bet ir reikšmingos domeno žinios kintamųjų parinkimui bei prielaidų tikrinimui.
Pavyzdžiui: siekiant prognozuoti buto kainą, modelyje gali būti aiškinamieji kintamieji kaip buto plotas, kambarių skaičius, vieta ir amžius. MK metodas leis rasti parametrus, kurie minimalizuoja prognozės klaidas mokymo duomenims, o vėlesnės diagnostikos padės patikrinti modelio prielaidas ir pritaikyti regresijos variantus (pvz., reguliarizaciją), jei reikia.
Ribotumai ir atsargumo priemonės
- Tiesinė regresija modeliuoja tik asociatyvius ryšius — ji savaime neįrodo priežastinumo.
- Netaisyklingos prielaidos (heteroskedastiškumas, autokoreliacija, stipri multikolineritytė) gali iškreipti standartinius klaidų įverčius ir lemti klaidingas išvadas, todėl būtini diagnostikos testai ir korekcinės priemonės.
- Perdėtas kintamųjų skaičius be pakankamai stebinių gali sukelti per didelį pritaikymą (overfitting); todėl naudingi kryžminės patikros (cross-validation) metodai ir reguliarizacija.
Santrauka
Tiesinė regresija yra paprastas ir galingas įrankis ryšiui tarp kintamųjų modeliuoti ir prognozuoti. Dažniausiai ji pritaikoma naudojant mažiausiųjų kvadratų metodą, tačiau svarbu tikrinti prielaidas, atlikti liekanų diagnostiką ir, esant reikalui, naudoti robustines ar reguliarizuotas alternatyvas. Kaip nurodyta aukščiau, terminai "mažiausiųjų kvadratų" ir "tiesinis modelis" yra glaudžiai susiję, bet ne visada sinonimai — MK metodas gali būti taikomas ir platesniam modeliavimo spektrui.
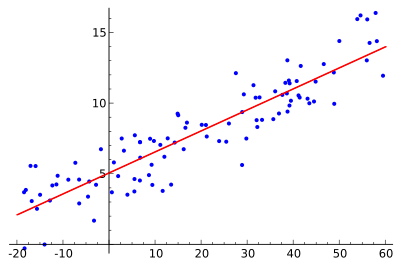
Siekiama rasti raudonąją kreivę, o mėlyni taškai yra tikrieji pavyzdžiai. Naudojant tiesinę regresiją visus taškus galima sujungti viena tiesia linija. Šiame pavyzdyje naudojama paprasta tiesinė regresija, kai atstumo tarp raudonos linijos ir kiekvieno imties taško kvadratas yra minimizuojamas.
Naudojimas
Ekonomika
Tiesinė regresija yra pagrindinė analizės priemonė ekonomikoje. Pavyzdžiui, ji naudojama vartojimo išlaidoms, išlaidoms investicijoms į ilgalaikį turtą, investicijoms į atsargas, šalies eksporto pirkimams, išlaidoms importui, likvidaus turto paklausai, darbo jėgos paklausai ir darbo jėgos pasiūlai nustatyti.
Klausimai ir atsakymai
K: Kas yra tiesinė regresija?
A: Linijinė regresija - tai būdas matematikos pagalba pažvelgti, kaip kas nors keičiasi, kai keičiasi kiti dalykai. Joje naudojamas priklausomas kintamasis ir vienas ar daugiau aiškinamųjų kintamųjų, kad būtų sudaryta tiesė, vadinama "regresijos linija".
K: Kokie yra tiesinės regresijos privalumai?
A: Modelius, kurie tiesiškai priklauso nuo savo nežinomų parametrų, lengviau pritaikyti negu modelius, kurie su savo parametrais susiję netiesiškai. Be to, lengviau nustatyti gautų įverčių statistines savybes.
K: Kokie yra praktiniai tiesinės regresijos panaudojimo būdai?
A: Tiesinė regresija gali būti naudojama norint pritaikyti prognozavimo modelį stebimoms reikšmėms (duomenims), kad būtų galima prognozuoti, numatyti ar sumažinti. Ji taip pat gali būti naudojama norint kiekybiškai įvertinti ryšių tarp kintamųjų stiprumą ir nustatyti duomenų pogrupius, kuriuose yra perteklinės informacijos apie kitą kintamąjį.
Klausimas: Kaip tiesinės regresijos modeliais stengiamasi sumažinti paklaidas?
A: Tiesinės regresijos modeliais stengiamasi, kad vertikalusis atstumas tarp tiesės ir duomenų taškų (liekanų) būtų kuo mažesnis. Tai daroma minimizuojant arba liekanų kvadratų sumą (mažiausiųjų kvadratų), arba nesutapimą pagal kokią nors kitą normą (mažiausius absoliutinius nuokrypius), arba minimizuojant mažiausiųjų kvadratų nuostolių funkcijos penalizuotą versiją (ridge regresija).
Klausimas: Ar įmanoma, kad tiesinės regresijos modeliai nebūtų grindžiami mažiausiųjų kvadratų principu?
A.: Taip, įmanoma, kad tiesinės regresijos modeliai nebūtų grindžiami mažiausiųjų kvadratų metodu, o būtų naudojami tokie metodai kaip nesutapimo minimizavimas pagal kokią nors kitą normą (mažiausi absoliutiniai nuokrypiai) arba mažiausiųjų kvadratų nuostolių funkcijos baudos minimizavimas (ridge regresija).
Klausimas: Ar "tiesinis modelis" ir "mažiausių kvadratų" yra sinonimai?
Atsakymas: Ne, tai nėra sinonimai. Nors jie glaudžiai susiję, "tiesinis modelis" reiškia būtent tiesės naudojimą, o "mažiausių kvadratų" reiškia būtent bandymą sumažinti klaidas, užtikrinant, kad tarp tiesės ir duomenų taškų būtų minimalus vertikalus atstumas.
Ieškoti