Matricų mechanika: kvantinės fizikos matricinė forma (Heisenbergas)
Atraskite Matricų mechaniką: Heisenbergo matricinė kvantinės fizikos forma, jos istorija, pritaikymai ir neapibrėžtumo principo reikšmė.
Matricų mechanika – tai pirmasis fizikų atrastas matematinis būdas išreikšti kvantinę fiziką. Werneris Heisenbergas iš pradžių sukūrė šią dėsnių išraiškos formą kaip skaičiavimo metodą, skirtą prognozuoti fotonų intensyvumą įvairiose vandenilio spektro juostose. 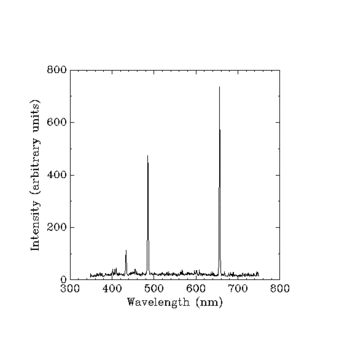
 Jo formulės aprašė tik matomus pereinamus energetinius lygius ir susijusias intensyvumo santykas, be prielaidų apie trajektorijas ar bangas klasikine prasme.
Jo formulės aprašė tik matomus pereinamus energetinius lygius ir susijusias intensyvumo santykas, be prielaidų apie trajektorijas ar bangas klasikine prasme.
Kaip atsirado matricų mechanika
Heisenbergo lygtis atrodė kaip sistema keliasdešimčiai kintamųjų ryšių; Maksas Bornas (Max Born) pastebėjo, kad šie ryšiai atitinka matricų dauginimą ir papildomai padėjo formuluoti teoriją griežtesne algebra. Kartu su Pascualu Jordanu buvo sukurta visa matricinė teorijos forma, kuri leido pažymėti matricas kaip operatorius, veikiančius kvantinių sistemų būsenas.
Kas yra matricos šioje teorijoje?
Matricų mechanikoje fizikiniai dydžiai (pvz., energija, momentas, vieta, kampinis momentas) aprašomi kaip matricos arba operatoriai. Matricos elementai susiję su pereinamuoju ryšiu tarp kvantinių būsenų — jų amplitudėmis ir fazėmis. Matricos dauginti reikia sekančia tvarka; šis dauginimas paprastai nėra komutatyvus, t. y. AB ≠ BA. Šis nekomutatyvumas yra kertinis kvantinės elgsenos bruožas.
Operatoriai, matricos ir matricos elementai
- Operatoriai veikia būsenų vektorius (matricų mechanikoje būsenos dažnai reprezentuojamos kaip stulpelinės matricos arba vektoriai).
- Eigenverčių (eigenvalue) idėja: matricos eigenreikšmės atitinka matuojamus kiekius (pvz., energijos lygmenis), o atitinkami eigenvektoriai – stabilią matavimo rezultatą duodančias būsenas.
- Komutatorius [A,B] = AB − BA: jei komutatorius nulis, dydžiai gali būti vienu metu tiksliai žinomi; jei ne, tarp jų egzistuoja kvantinė apribojimo ryšys (neapibrėžtumo ryšys).
Neapibrėžtumo principas
Netrukus po matricinės teorijos paskelbimo vienas svarbiausių jos rezultatų tapo Heisenbergo neapibrėžtumo principas. Paprastai jis formuluojamas taip: vietos ir momento paklaidos susijusios ryšiu Δx·Δp ≥ ħ/2 (čia ħ yra sumažintas Planko konstanta). Šis ryšys kyla tiesiogiai iš operatorių nekomutatyvumo — tai nėra matavimo klaidos pasekmė, o elementarus kvantinės gamtos bruožas.
Heisenbergo (matricų) paveikslas ir Schrödingerio paveikslas
Matricų mechanika iš esmės atspindi tą pačią fiziką kaip ir Erwino Schrödingerio banginė mechanika: abi formuluotės duoda tokius pačius eksperimentinius spėjimus ir yra matematiškai ekvivalentžios. Skirtumas – vaizdavime:
- Heisenbergo (matricų) paveikslas: operatoriai (matricos) priklauso nuo laiko, o kvantiniai būsenų vektoriai laikui bėgant nekinta.
- Schrödingerio paveikslas: operatoriai yra fiksuoti, o būsenos evoliucionuoja pagal Schrödingerio lygtį (banginė funkcija keičiasi laike).
Abu paveikslai suteikia skirtingas komforto zonas: matricų mechanika ypač patogi, kai reikia dirbti su diskrečiais spektriniais lygmenimis, kampiniu momentu ir spinų sistemomis; banginė mechanika dažnai patogesnė erdvinių bangų ir potencialų problems sprendimui.
Pritaikymai ir pavyzdžiai
- Harmoningas svyravimas: matricų mechanikoje problemą sprendžiant naudojami pakėlimo ir nuleidimo operatoriai, kas leidžia aiškiai gauti energijos lygius.
- Kampinis momentas ir spinai: kampinio momento matricos leidžia patogiai rasti leidžiamus kvantinius skaičius (m, l), o dviejų lygių sistemos (pvz., elektronų spinai) dažnai modeliuojamos 2×2 matricomis (Pauli matricomis).
- Spektrų prognozavimas: Heisenbergas pradžioje panaudojo matricinę formulę, kad apskaičiuotų vandenilio spektro linijų intensyvumus ir dažnius, sudarydamas ryšį tarp perėjimų tarp energijos lygmenų.
Istorinis ir koncepcinis reikšmingumas
Matricų mechanika pakeitė klasikinių sąvokų supratimą: vietoje deterministinių trajektorijų įvedė operatorinę ir statistinę perspektyvą. Maksas Bornas, Pascualas Jordanas ir Paulis Diracas (tarp kitų) išplėtė ir formalizavo teoriją, o Bornas vėliau pasiūlė ir probabilistinę banginės funkcijos interpretaciją. Matricų mechanika padėjo pagrindus moderniai kvantų teorijai bei operatorių algebrai, kurie dabar yra plačiai taikomi tiek fundamentinėje fizikoje, tiek taikomojoje kvantinės mechanikos inžinerijoje.
Santrauka: Matricų mechanika – tai operatorinė (matricinė) kvantinės mechanikos forma, kuri akcentuoja nekomutatyvius operatorius, kvantinius energijos lygius ir natūraliai veda prie tokių reiškinių kaip neapibrėžtumo principas. Nors egzistuoja kelios formalios kvantinės mechanikos formuluotės, matricų mechanika išlieka svarbi tiek istorine, tiek praktine prasme.
Klausimai ir atsakymai
K: Kas yra matricinė mechanika?
A: Matricų mechanika - tai Vernerio Heizenbergo (Werner Heisenberg) sukurta fizikos dėsnių išraiškos forma, kuri naudoja matricas fotonų intensyvumui įvairiose vandenilio spektro juostose nusakyti.
K: Kas sukūrė matricinę mechaniką?
A: Werneris Heisenbergas iš pradžių sukūrė matricos mechaniką kaip lygtį, skirtą fotonų intensyvumui įvairiose vandenilio spektro juostose numatyti.
K: Kaip jis buvo aptiktas?
A: Maksas Bornas pastebėjo, kad Heizenbergo lygtis iš esmės yra matricų kūrimo ir dauginimo schema, todėl buvo atrasta matricų mechanika.
K: Ar jis vis dar naudojamas šiandien?
Atsakymas: Taip, matricinė mechanika tebenaudojama ir šiandien, nes ji yra naudinga ir patogi tam tikriems tikslams.
K: Ar yra kitų matematinių būdų kvantinei fizikai išreikšti?
Atsakymas: Taip, Erwino Schrödingerio lygtis, kurioje naudojama Erwino Schrödingerio banginė funkcija, yra matematiškai lygiavertė, tačiau ją paprasčiau naudoti kitais tikslais.
K.: Kokia buvo viena iš pirmųjų šios teorijos sėkmių?
A: Vienas iš pirmųjų su šia teorija susijusių laimėjimų buvo tai, kas dabar vadinama Heizenbergo neapibrėžtumo principu.
K: Kas paskelbė apie šią sėkmę netrukus po to, kai ji buvo sukurta?
Atsakymas: Pats Werneris Heisenbergas paskelbė apie šią sėkmę netrukus po to, kai ji buvo sukurta.
Ieškoti