Heizenbergo neapibrėžtumo principas

Sumaištis su stebėtojo poveikiu

Istoriškai neapibrėžtumo principas buvo painiojamas su šiek tiek panašiu poveikiu fizikoje, vadinamu stebėtojo efektu. Jis teigia, kad kai kurių sistemų matavimų negalima atlikti nedarant įtakos sistemoms. Heizenbergas pasiūlė tokį stebėtojo efektą kvantiniame lygmenyje kaip fizikinį kvantinio neapibrėžtumo "paaiškinimą".

Tačiau dabar jau aišku, kad neapibrėžtumo principas yra visų banginių sistemų savybė. Jis atsiranda kvantinėje mechanikoje tiesiog dėl visų kvantinių objektų medžiagos banginės prigimties. Taigi, neapibrėžtumo principas iš tikrųjų nurodo esminę kvantinių sistemų savybę, o ne teiginį apie dabartinės technologijos stebėjimo sėkmę. "Matavimas" reiškia ne tik procesą, kuriame dalyvauja fizikas stebėtojas, bet ir bet kokią klasikinių ir kvantinių objektų sąveiką, nepriklausomai nuo bet kokio stebėtojo.

Neapibrėžtumo idėja

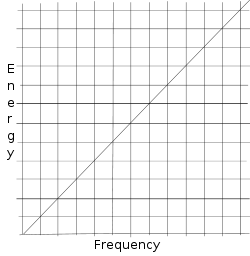
Neapibrėžtumo principas atsirado iš Vernerio Heizenbergo matricinės mechanikos. Maksas Plankas jau žinojo, kad šviesos vieneto energija yra proporcinga šviesos vieneto dažniui ( E ∝ ν {\displaystyle E\propto \nu } ) ir kad jo energijos kiekį galima išreikšti žinomais terminais, pavyzdžiui, džauliu, naudojant proporcingumo konstantą. Jo pateikta konstanta dabar vadinama Planko konstanta ir žymima raide h. Kai kvantinei mechanikai išreikšti naudojamos matricos, dažnai tenka padauginti dvi matricas, kad būtų gauta trečioji matrica, kuri duoda atsakymą, kurį fizikas bando rasti. Tačiau padauginus tokią matricą kaip P (impulsui) iš tokios matricos kaip X (padėčiai), gaunama kitokia atsakymo matrica nei ta, kuri gaunama padauginus X iš P. P padauginus P iš X ir X iš P, o paskui juos palyginus, rezultatas visada apima Planko konstantą kaip faktorių. Skaičius, naudojamas Plancko konstantai užrašyti, visada priklausys nuo naudojamos matavimo sistemos. (Naudojant tam tikrą matavimo sistemą, jos skaitinė reikšmė yra vienas.) Dešinėje esančios diagramos linijos, rodančios dažnio ir energijos santykį, nuolydis taip pat priklausys nuo pasirinktos matavimo sistemos.

Toliau pateiktose diagramose parodyta, kas atsitinka, kai bandome išmatuoti ir vietą, ir pagreitį.

Praktinis šio matematinio atradimo rezultatas yra tas, kad kai fizikas aiškiau nurodo padėtį, tada ir momentas tampa mažiau aiškus, o kai fizikas aiškiau nurodo momentą, tada ir padėtis tampa mažiau aiški. Heizenbergas sakė, kad dalykai yra "neapibrėžti", o kiti žmonės mėgo sakyti, kad jie yra "neapibrėžti". Tačiau matematika rodo, kad būtent pasaulio dalykai yra neapibrėžti arba "neaiškūs", o ne tai, kad tik žmonės nėra tikri dėl to, kas vyksta.

Plati skylė, ryškus fokusavimas


Sumažinus tarpą padidėja tikrumas, kad fotonas yra viduryje, tačiau jo judėjimo kryptis nuo jo iki aptikimo ekrano dešinėje tampa atitinkamai labiau neapibrėžta.


Siaura skylė, išsklaidytas fokusas


Spyruoklėmis pakabinus centrinį tarpą, galima išmatuoti impulsą, tačiau tarpas nenuspėjamai pasislenka, todėl informacija apie fotono buvimo vietą viduryje prarandama.


Spyruoklinės skylės matavimo momentas

Neapibrėžtumo pateikimas matematine forma

Čia pateiksime pirmąją lygtį, kuri suteikė pagrindinę idėją, vėliau parodytą Heizenbergo neapibrėžtumo principe.

1925 m. Heizenbergo novatoriškame straipsnyje nenaudojamos ir net neminimos matricos. Didžioji Heizenbergo sėkmė buvo "schema, pagal kurią iš principo buvo galima vienareikšmiškai nustatyti atitinkamas vandenilio spinduliuotės fizikines savybes (perėjimo dažnius ir amplitudes)".

Kai Heizenbergas parašė savo proveržio darbą, jis atidavė jį vienam iš savo mokytojų sutvarkyti ir išvyko atostogų. Maksą Borną suglumino lygtys ir nekomutacinės lygtys, kurios net Heizenbergui atrodė problema. Po kelių dienų Bornas suprato, kad šios lygtys buvo matricų užrašymo nurodymai. Matricos buvo naujos ir keistos net to meto matematikams, tačiau kaip su jomis skaičiuoti, jau buvo aiškiai žinoma. Jis ir dar keli kiti, prieš grįžtant Heizenbergui iš atostogų, viską išdėstė matricų pavidalu, ir per kelis mėnesius naujoji kvantinė mechanika matricų pavidalu tapo dar vieno darbo pagrindu.

Maksas Bornas pastebėjo, kad apskaičiavus pq ir qp vaizduojančias matricas, jos nebus lygios. Heizenbergas jau buvo pastebėjęs tą patį, kalbant apie jo pirminį užrašymo būdą, ir Heizenbergas galėjo numanyti tai, kas Bornui buvo beveik iš karto akivaizdu - kad skirtumas tarp atsakymų matricų pq ir qp visada bus susijęs su dviem veiksniais, kurie atsirado Heizenbergo pirminėje matematikoje: Planko konstanta h ir i, kuri yra kvadratinė šaknis iš neigiamo vieneto. Taigi pati idėja, kurią Heizenbergas norėjo vadinti "neapibrėžtumo principu" (paprastai vadinama neapibrėžtumo principu), slypėjo pirminėse Heizenbergo lygtyse.

Heizenbergas nagrinėjo pokyčius, kurie vyksta atome, kai elektronas pakeičia savo energijos lygį ir taip priartėja prie atomo centro arba nutolsta nuo jo, ir ypač situacijas, kai elektronas dviem etapais nukrenta į žemesnę energijos būseną. Maksas Bornas paaiškino, kaip jis pasinaudojo keistu Heizenbergo "receptu", kaip rasti tam tikro pokyčio atome iš energijos lygio n į energijos lygį n-b sandaugą C, t. y. paimti sumą, padauginus vieną pokytį, vadinamą A (tai gali būti, pavyzdžiui, fotono dažnis), atsiradusį dėl elektrono energijos pokyčio atome iš energijos būsenos n į energijos būseną n-a), iš kito pokyčio, vadinamo B (tai gali būti, pavyzdžiui, pokyčio amplitudė), atsiradusio dėl kito energijos būsenos pokyčio iš n-a į n-b):

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

ir atrado kai ką novatoriško:

Nagrinėdamas ... pavyzdžius... [Heizenbergas] nustatė šią taisyklę.... Tai buvo 1925 m. vasarą. Heizenbergas... pasiėmė atostogų... ir perdavė savo darbą man paskelbti....

Heizenbergo daugybos taisyklė nepaliko man ramybėje, o po savaitės intensyvių apmąstymų ir bandymų staiga prisiminiau algebros teoriją....Tokie kvadratiniai masyvai matematikams gana gerai pažįstami ir vadinami matricomis, siejant su tam tikra daugybos taisykle. Šią taisyklę pritaikiau Heizenbergo kvantinei sąlygai ir nustačiau, kad ji sutampa su įstrižainės elementais. Buvo lengva atspėti, kokie turi būti likę elementai, t. y. nuliniai, ir iš karto prieš mane iškilo keista formulė

Q P - P Q = i h 2 π {\displaystyle {QP-PQ={\frac {ih}{2\pi }}}}
[Simbolis Q - poslinkio matrica, P - impulso matrica, i reiškia kvadratinę šaknį iš neigiamo vieneto, o h - Planko konstantą].

Vėliau Heizenbergas savo atradimą pavertė kita matematine forma:

Δ x Δ p ≥ ℏ 2 {\displaystyle \Delta x\,\Delta p\geq {\frac {\hbar }{2}}}

(Specialus simbolis ℏ {\displaystyle {\hbar }} vadinamas "h-bar" arba "redukuota Plankso konstanta" ir yra lygus h 2 π {\displaystyle {\frac {h}{2\pi }}} .)

Matematika yra būdas apibūdinti dalykus, kurie vyksta realiame pasaulyje. Galite įsivaizduoti, kad būtų lengva vienu metu gauti ir tikslią daikto padėtį, ir jo tikslią masę, kelią bei greitį. Tačiau tikrovėje, norėdami gauti atsakymą, turite atlikti du dalykus. Jei matuojate kulkos, įstrigusios kažkur didžiulio kalno uoloje, padėtį ir pagreitį, tai yra paprastas dalykas. Atrodo, kad kalnas niekur nejuda, kaip ir kulka. Taigi jos padėtis yra žinoma, o greitis lygus 0, taigi ir jos pagreitis taip pat lygus 0. Tačiau jei kulka yra kažkur tarp šautuvo ir taikinio, bus sunku nustatyti jos padėtį bet kuriuo metu. Geriausia, ką galime padaryti, tai nufotografuoti ją fotoaparatu su labai greitu užraktu. Tačiau vieną kartą nuspaudus užraktą gautume tik vieną rezultatą - kulkos padėtį laike t. Kad gautume momentą, kulkai kelią galėtume pastatyti parafino bloką ir išmatuoti, kaip parafino blokas judėjo, kai jis sustabdė kulką. Arba, jei žinotume kulkos masę, galėtume padaryti dviejų nuotraukų seką, apskaičiuoti greitį žinodami skirtumą tarp dviejų kulkos padėčių ir laiko tarp dviejų jos pasirodymų. Kad ir kaip tai darytume, turime išmatuoti masę, padėtį ir laiką tarp pasirodymų. Kad gautume x ir p, turime atlikti bent du matavimus. Tokiu atveju turime pasirinkti, kurį matavimą atlikti pirmą, o kurį - antrą. Atrodo, kad nėra jokio skirtumo, kokia tvarka atliekame matavimus. Išmatuoti kulkos masę ir tada du kartus išmatuoti jos padėtį arba du kartus išmatuoti kulkos padėtį, o tada kulką susigrąžinti ir išmatuoti jos masę, juk nebūtų jokio skirtumo, ar ne? Juk svėrę kulką ar ją fotografuodami nieko nedarėme su kulka.

Tačiau labai mažu masteliu, kai matuojame tokį daiktą kaip elektronas, kiekvienas matavimas jį kažkiek paveikia. Jei pirmiausia išmatuojame padėtį, tuomet keičiame jo momemtum. Jei pirmiausia išmatuojame elektrono momentą, tuomet proceso metu pakeičiame jo padėtį. Mūsų viltis būtų išmatuoti vieną iš jų, o tada išmatuoti kitą, kol niekas nepasikeitė, tačiau pats matavimas sukelia pokyčius, ir geriausia, ko galime tikėtis, tai sumažinti iki minimumo energiją, kurią įnešame į elektroną jį matuodami. Šis minimalus energijos kiekis turi Planko konstantą kaip vieną iš veiksnių.

Neapibrėžtumas peržengia matricų matematikos ribas

Heizenbergo neapibrėžtumo principas buvo rastas pirmosiose "naujosios" kvantinės fizikos lygtyse, o teorija buvo pateikta naudojant matricų matematiką. Tačiau neapibrėžtumo principas yra gamtos faktas, ir jis atsiskleidžia kitais būdais kalbant apie kvantinę fiziką, pavyzdžiui, Erwino Schrödingerio sudarytose lygtyse.

Gamtos neapibrėžtumas, o ne žmonių neapibrėžtumas

Į Heizenbergo atradimą buvo pažvelgta dviem labai skirtingais būdais: Vieni žmonės mano, kad gamtoje vykstantys dalykai yra "determinuoti", t. y. viskas vyksta pagal tam tikrą taisyklę, ir jei žinotume viską, ką reikia žinoti, visada galėtume pasakyti, kas bus toliau. Kiti žmonės mano, kad gamtoje vykstančius dalykus lemia tik tikimybė, ir mes galime žinoti tik tai, kaip dalykai elgsis vidutiniškai - bet mes tai žinome labai tiksliai.

Fizikas Johnas Stewartas Bellas atrado būdą įrodyti, kad pirmasis būdas negali būti teisingas. Jo darbas vadinamas Bello teorema arba Bello nelygybe.

Populiarioji kultūra

Pasakymas "kvantinis šuolis" arba "kvantinis šuolis" reiškia didelius ir permainingus pokyčius ir dažnai vartojamas hiperbolizuotai politikų ir žiniasklaidos pardavimo kampanijose. Kvantinėje mechanikoje jis vartojamas apibūdinti elektrono perėjimui iš vienos orbitos aplink atomo branduolį į bet kurią kitą, aukštesnę ar žemesnę, orbitą.

Kartais žodis "quantum" vartojamas komercinių produktų ir įmonių pavadinimuose. Pavyzdžiui, "Briggs and Stratton" gamina daugybę rūšių mažų benzininių variklių, skirtų vejapjovėms, rotaciniams kultivatoriams ir kitoms panašioms mažoms mašinoms. Vienas iš jų modelių pavadinimų yra "Quantum".

Kadangi neapibrėžtumo principas sako, kad tam tikri matavimai atomų lygmenyje negali būti atliekami nesutrikdant kitų matavimų, kai kurie žmonės naudoja šią idėją apibūdindami atvejus žmonių pasaulyje, kai stebėtojo veikla keičia stebimą dalyką. Antropologas gali nuvykti į kokią nors tolimą vietą, kad sužinotų, kaip ten gyvena žmonės, tačiau tai, kad juos stebi svetimas žmogus iš išorinio pasaulio, gali pakeisti tų žmonių elgesį.

Tai, ką žmonės daro stebėdami dalykus, kurie keičia tai, kas stebima, yra stebėtojo efekto atvejai. Kai kurie dalykai, kuriuos daro žmonės, sukelia pokyčius labai mažame atomų lygmenyje ir yra neapibrėžtumo arba neapibrėžtumo atvejai, kuriuos pirmasis aprašė Heizenbergas. Neapibrėžtumo principas rodo, kad visada egzistuoja riba, iki kurios galime atlikti tam tikras matavimų poras, pavyzdžiui, padėties ir greičio arba trajektorijos ir impulso matavimus. Stebėtojo efektas sako, kad kartais tai, ką žmonės daro stebėdami dalykus, pavyzdžiui, sužinodami apie skruzdėlių koloniją, iškasdami ją sodo įrankiais, gali turėti didelį poveikį, kuris pakeičia tai, ką jie bandė sužinoti.