Planko konstanta

Fonas

Šiame straipsnyje naudojami simboliai.
Simbolis Reikšmė E Energija h Planko konstanta k Boltzmanno konstanta c šviesos greitis λ spinduliuotės bangos ilgis ν spinduliavimo dažnis T absoliuti temperatūra

1670-1900 m. mokslininkai diskutavo apie šviesos prigimtį. Kai kurie mokslininkai manė, kad šviesą sudaro daugybė milijonų mažų dalelių. Kiti mokslininkai manė, kad šviesa yra banga.

Šviesa: bangos ar dalelės?

1678 m. Christiaanas Huygensas parašė knygą Traité de la lumiere ("Traktatas apie šviesą"). Jis manė, kad šviesa susideda iš bangų. Jis teigė, kad šviesa negali būti sudaryta iš dalelių, nes dviejų spindulių šviesa neatsispindi viena nuo kitos. 1672 m. Izaokas Niutonas parašė knygą "Optika". Jis manė, kad šviesą sudaro raudonos, geltonos ir mėlynos spalvos dalelės, kurias jis vadino kūneliais. Niutonas tai paaiškino savo "dviejų prizmių eksperimentu". Pirmoji prizmė suskaldė šviesą į skirtingas spalvas. Antroji prizmė šias spalvas vėl sujungė į baltą šviesą.

XVIII a. daugiausia dėmesio buvo skiriama Niutono teorijai. 1803 m. Tomas Youngas aprašė "dvigubo plyšio eksperimentą". Šio eksperimento metu šviesa, einanti pro du siaurus plyšius, interferuoja pati su savimi. Dėl to susidaro modelis, rodantis, kad šviesa sudaryta iš bangų. Visą likusį XIX a. šviesos bangų teorijai buvo skiriama daugiausia dėmesio. XIX a. šeštajame dešimtmetyje Džeimsas Klerkas Maksvelas (James Clerk Maxwell) sukūrė lygtis, kurios elektromagnetinę spinduliuotę apibūdino kaip bangas.

Elektromagnetinės spinduliuotės teorijoje šviesa, radijo bangos, mikrobangos ir daugelis kitų rūšių bangų laikomos tuo pačiu dalyku, išskyrus tai, kad jų bangų ilgiai skiriasi. Šviesos, kurią matome akimis, bangos ilgis yra maždaug 400-600 nm. Radijo bangų bangos ilgis svyruoja nuo 10 m iki 1500 m, o mikrobangų - apie 2 cm. Vakuume visos elektromagnetinės bangos sklinda šviesos greičiu. Elektromagnetinės bangos dažnį nusako formulė:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}}.

Simboliai apibrėžiami čia.

Juodi kėbulo radiatoriai

Visi šilti daiktai skleidžia šiluminę spinduliuotę, kuri yra elektromagnetinė spinduliuotė. Dauguma Žemėje esančių daiktų skleidžia infraraudonąją spinduliuotę, tačiau labai karšti daiktai (1000 °C ar daugiau) skleidžia matomąją spinduliuotę, t. y. šviesą. XIX a. pabaigoje daugelis mokslininkų tyrinėjo elektromagnetinės spinduliuotės bangų ilgius, kuriuos skleidžia įvairios temperatūros juodųjų kūnų spinduliai.

Rayleigh-Jeans teisė

Lordas Rayleigh pirmą kartą paskelbė Rayleigh-Jeans dėsnio pagrindus 1900 m. Ši teorija buvo pagrįsta kinetine dujų teorija. 1905 m. seras Džeimsas Džeinsas paskelbė išsamesnę teoriją. Dėsnis susieja elektromagnetinės energijos, kurią skleidžia skirtingos temperatūros juodojo kūno radiatorius, kiekį ir bangos ilgį. Jį apibūdinanti lygtis yra tokia:

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}}.

Pagal šią lygtį prognozuojami ilgųjų bangų spinduliuotės rezultatai gerai atitiko laboratorijoje gautus praktinius rezultatus. Tačiau trumpų bangų ilgių (ultravioletinių spindulių) atveju skirtumas tarp teorijos ir praktikos buvo toks didelis, kad buvo pramintas "ultravioletine katastrofa".

Planko dėsnis

1895 m. Wienas paskelbė savo tyrimų apie juodojo kūno spinduliuotę rezultatus. Jo formulė buvo tokia:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}} .

Ši formulė gerai veikė trumpųjų bangų elektromagnetinei spinduliuotei, tačiau neveikė gerai ilgųjų bangų atveju.

1900 m. Maxas Planckas paskelbė savo tyrimų rezultatus. Jis bandė sukurti juodojo kūno spinduliuotės išraišką, išreikštą bangos ilgiu, darydamas prielaidą, kad spinduliuotė susideda iš mažų kvantų, ir bandė išsiaiškinti, kas atsitiktų, jei kvantai taptų be galo maži. (Tai standartinis matematinis metodas). Išraiška buvo tokia:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}}}.

Jei šviesos bangos ilgis gali būti labai didelis, galima įrodyti, kad Ralio-Džanso ir Planko sąryšiai beveik sutampa.

Jis apskaičiavo h ir k ir nustatė, kad

h = 6,55×10⁻²⁷ erg-sek.

k = 1,34×10⁻¹⁶erg-deg ^-1.

Šios vertės yra artimos šiuolaikinėms priimtinoms vertėms, ⁻¹⁶atitinkamai 6,62606×10⁻³⁴ ir 1,38065×10. Planko dėsnis gerai sutampa su eksperimentiniais duomenimis, tačiau visa jo reikšmė buvo įvertinta tik po kelerių metų.

Kvantinė šviesos teorija

Pasirodo, kad elektronai išsiskiria dėl fotoelektrinio efekto, jei šviesa pasiekia slenkstinį dažnį. Žemiau šio dažnio iš metalo negali išsiskirti jokie elektronai. 1905 m. Albertas Einšteinas paskelbė straipsnį, kuriame paaiškino šį efektą. Einšteinas pasiūlė, kad šviesos pluoštas yra ne erdvėje sklindanti banga, o diskrečių bangų paketų (fotonų), kurių kiekvienas turi energiją, rinkinys. Einšteinas teigė, kad efektas atsirado dėl fotono smūgio į elektroną. Tai įrodė šviesos dalelių prigimtį.

Einšteinas taip pat nustatė, kad didelio bangos ilgio elektromagnetinė spinduliuotė neturi jokio poveikio. Einšteinas teigė, kad taip atsitiko todėl, kad "dalelės" neturėjo pakankamai energijos, kad sutrikdytų elektronus.

Plankas pasiūlė, kad kiekvieno fotono energiją su fotono dažniu sieja Planko konstanta. Matematiškai tai galima užrašyti taip:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}}.

1918 m. Plankui buvo paskirta Nobelio premija už nuopelnus fizikos pažangai, kuriuos jis padarė atradęs energijos kvantus. 1921 m. Einšteinas gavo Nobelio premiją už tai, kad susiejo Planko konstantą su fotoelektriniu efektu.

Iliustracija paimta iš originalaus Niutono laiško Karališkajai draugijai (1671 m. sausio 1 d. [pagal Julijaus kalendorių]). S reiškia saulės šviesą. Šviesa tarp plokštumų BC ir DE yra spalvota. Šios spalvos rekombinuojamos ir sudaro saulės šviesą plokštumoje GH


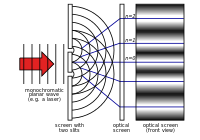
Youngo dvigubo plyšio eksperimentas


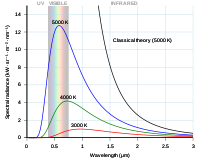
Reilėjaus-Džanso kreivė ir Planko kreivė, nubrėžtos pagal fotono bangos ilgį.


1911 m. Solvėjaus konferencija. Stovi Planckas, Einšteinas ir Džeinsas. Planckas yra antras iš kairės. Einšteinas - antras iš dešinės. Džinsas penktas iš dešinės. Wienas sėdi trečias iš dešinės.

Paraiška

Planko konstanta yra svarbi daugeliui taikymų. Keletas jų išvardyta toliau.

Boro atomo modelis

1913 m. Nielsas Boras paskelbė Boro atomo struktūros modelį. Boras teigė, kad aplink branduolį besisukančių elektronų kampinis momentas gali turėti tik tam tikras reikšmes. Šias vertes nusako lygtis

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}

kur

L = su lygiu susijęs kampinis momentas.

n = teigiamas sveikasis skaičius.

h = Planko konstanta.

Pagal Boro atomo modelį galima apskaičiuoti elektronų energiją kiekviename lygmenyje. Paprastai elektronai užpildo mažiausią skaičių turinčias atomo būsenas. Jei atomas gauna energijos, pavyzdžiui, iš elektros srovės, elektronai bus sužadinti į aukštesnę būseną. Tada elektronai vėl nukris į žemesnę būseną, o papildomos energijos neteks išskirdami fotoną. Kadangi energijos lygmenys turi konkrečias vertes, fotonai turės konkrečius energijos lygmenis. Tokiu būdu išspinduliuotą šviesą galima suskaidyti į skirtingas spalvas naudojant prizmę. Kiekvienas elementas turi savo raštą. Neono raštas parodytas šalia.

Heizenbergo neapibrėžtumo principas

1927 m. Werneris Heisenbergas paskelbė neapibrėžtumo principą. Šis principas teigia, kad neįmanoma atlikti matavimo nesutrikdant matuojamo dalyko. Jis taip pat nustato mažiausio trikdymo, kurį sukelia matavimas, ribą.

Makroskopiniame pasaulyje šie trikdžiai nedaug ką keičia. Pavyzdžiui, jei matuojama skysčio kolbos temperatūra, termometras įkaitęs sugeria nedidelį energijos kiekį. Dėl to galutiniai rodmenys bus šiek tiek paklaidinti, tačiau ši paklaida yra nedidelė ir nesvarbi.

Kvantinėje mechanikoje yra kitaip. Kai kurie matavimai atliekami žiūrint į išsklaidytų fotonų modelį. Vienas iš tokių pavyzdžių yra Komptono sklaida. Jei matuojama ir dalelės padėtis, ir judesys, neapibrėžtumo principas teigia, kad egzistuoja kompromisas tarp judesio matavimo tikslumo ir padėties matavimo tikslumo. Šį kompromisą apibūdina tokia lygtis:

Δ x x Δ p ≳ h {\displaystyle \Delta x\,\Delta p\gtrsim h\qquad \qquad \qquad }

kur

Δp = momento neapibrėžtis.

Δx = padėties neapibrėžtis.

h = Planko konstanta.

Šviesos diodų spalva

Dešinėje pavaizduotoje elektrinėje grandinėje įtampos kritimas ant šviesos diodo (LED) priklauso nuo LED medžiagos. Silicio diodų įtampos kritimas yra 0,6 V. Tačiau šviesos diodų įtampos kritimas yra nuo 1,8 V iki 2,7 V. Ši informacija leidžia vartotojui apskaičiuoti Planko konstantą.

Energija, kurios reikia, kad vienas elektronas peršoktų potencialo barjerą LED medžiagoje, yra lygi

E = Q e V L {\displaystyle E=Q_{e}V_{L}\,}

kur

Q_e yra vieno elektrono krūvis.

V_L - įtampos kritimas šviesos diode.

Kai elektronas vėl suyra, jis išspinduliuoja vieną šviesos fotoną. Fotono energija nustatoma pagal tą pačią lygtį, kuri naudojama fotoelektriniam efektui. Sujungus šias lygtis, šviesos bangos ilgis ir įtampa yra susiję taip

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}}},}

Pagal šį santykį galima apskaičiuoti toliau pateiktą lentelę.

Spalva	Bangos ilgis (nm)	Įtampa
raudona šviesa	650	1.89
žalia šviesa	550	2.25
mėlyna šviesa	470	2.62

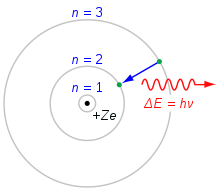
Boro atomo modelis. Elektronas, krintantis iš n=3 apvalkalo į n=2 apvalkalą, praranda energiją. Ši energija nunešama kaip vienas fotonas.


Neono regimasis spektras. Kiekviena linija žymi skirtingą energijos lygmenų porą.


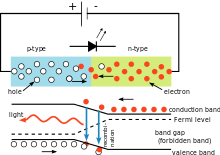
Paprasta LED grandinė, iliustruojanti Planko konstantos naudojimą. Spinduliuojamos šviesos spalva priklauso nuo įtampos kritimo ant diodo. Šviesos bangos ilgį galima apskaičiuoti naudojant Planko konstantą.

Planko konstantos vertė ir kilogramo apibrėžimas iš naujo

Nuo tada, kai h buvo atrastas, jo matavimai tapo daug geresni. Planckas pirmą kartą nurodė, kad h vertė yra 6,55×10 ⁻²⁷erg-sek. Ši vertė yra 5 % mažesnė už dabartinę.

2014 m. kovo 3 d. duomenimis, geriausia išmatuota h vertė SI vienetais yra 6,62606957×10 ⁻³⁴J-s. Atitinkamas skaičius CGS vienetais yra 6,62606957×10 ⁻²⁷erg-sek. Santykinė h neapibrėžtis yra 4,4×10 ⁻⁸.

Sumažinta Planko konstanta (ħ) - tai vertė, kuri kartais naudojama kvantinėje mechanikoje. Ji apibrėžiama taip

ℏ = h 2 π {displaystyle \hbar ={\frac {h}{2\pi }}}.

Kvantinėje mechanikoje vietoj SI kartais naudojami Planko vienetai. Šioje sistemoje redukuotoji Planko konstanta yra lygi 1, taigi Planko konstantos vertė yra 2π.

Dabar galima labai tiksliai išmatuoti Plancko konstantą. Tai paskatino BIPM apsvarstyti naują kilogramo apibrėžtį. Kilogramui apibrėžti nebenaudojamas tarptautinis kilogramo prototipas. Vietoj to BIPM nustatė tikslią Plancko konstantos vertę. Mokslininkai, apibrėždami kilogramą, naudoja šią vertę ir metro bei sekundės apibrėžimus.

 

Teorinės Planko konstantos vertė

Planko konstantą taip pat galima išvesti matematiškai:

 

h = μ 0 π 12 c 3 [ q 0 [ 0,9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6,63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}{[{q_{0}}}{[0,9163a_{0}]}^{2}]^{2}}{f_{1r}}^{5}\cdot {s}=6,63\ kartų 10^{-34}J\cdot s}

Čia μ 0 {\displaystyle \mu _{0}} yra laisvosios erdvės pralaidumas, c {\displaystyle c} yra šviesos greitis, q 0 {\displaystyle q_{0}} yra elektrono elektros krūvis, a 0 {\displaystyle a_{0}} yra Boro spindulys, o f 1 r {\displaystyle f_{1r}} yra elektrono sukimosi dažnis vandenilio atome ( f 1 r = 3.29 × 10 15 r e v / s ) {\displaystyle (f_{1r}=3,29\ kartus 10^{15}rev/s)} . Šias konstantų vertes pakeitus į teorinę Planko konstantą, teorinė Planko konstantos vertė yra tiksliai lygi eksperimentinei vertei.

Susiję puslapiai

• Bangų ir dalelių dualumas