Heizenbergo neapibrėžtumo sąryšis

Diagramos

6. Šioje animacijoje parodyta viena iš svarbių visatos neapibrėžtumo pasekmių - kvantinis elektronų tuneliavimas. Atidžiai įsižiūrėkite. Kiekvieną kartą pro barjerą prasiskverbia po truputį.


5. Pakabinus centrinį tarpą spyruoklinėmis svarstyklėmis, galima išmatuoti impulsą, tačiau tai darant tarpas neprognozuojamai pasislenka, todėl informacija apie kiekvieno fotono buvimo vietą viduryje prarandama.


4. Spyruoklė, pritvirtinta prie barjero su maža skylute, priverčia dalelę išsprūsti pro skylutę, kuri stumia barjerą, ištempia spyruokles ir taip išmatuoja impulsą. Tačiau dėl to, kad spyruoklėmis pritvirtinta užtvara juda, esame mažiau tikri, kurioje vietoje dalelė buvo, kai išlindo pro skylutę, be to, difrakcija taip pat turės įtakos jos padėčiai aptikimo ekrane.


3. Susiaurinus skylę padidėja tikrumas, kad fotonas yra viduryje, tačiau jo judėjimo kryptis nuo šios vietos iki aptikimo ekrano dešinėje tampa atitinkamai labiau neapibrėžta. Fokusas tampa neryškus. Išplėtus skylę, visi fotonai atsiduria aptikimo ekrano centre, tačiau tada mažiau tiksliai žinome, kur jie buvo, kai prasiskverbė pro centrinę užtvarą.


1. Fotonai, elektronai ir kitos subatominės dalelės, iššautos pro didelę skylę, atsidurs aštriame fokuse, tačiau mes tiksliai nežinome, kurioje vietoje jos buvo viduryje kelio.


2. Siaurinant skylę, dalelių keliai ties skylės kraštais sulenkiami (difrakcija), todėl gaunamas spindulys tampa didesnis ir švelnesnis.

Kaip žmonės sužinojo apie neapibrėžtumą?

Netrukus po to, kai Verneris Heizenbergas sukūrė naująją kvantinę fiziką, iš jo matematikos išplaukė netikėta frazė:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }}\qquad \qquad \qquad }

Padėties (x) paklaidos intervalas, padaugintas iš impulso (p) paklaidos intervalo, yra maždaug lygus arba didesnis už Planko konstantą, padalytą iš 4π.

Šie simboliai matematine forma išreiškia tai, ką jau matėte paveikslėliuose. Šie simboliai aiškiai sako, kad negalima būti visiškai tikriems, kur kas nors yra ir kur tai eina. Jei bet kuriuo metu aiškiau suvokiate, kur jis yra, tuomet mažiau įsivaizduojate, kur jis eina ir kaip greitai. Jei bet kuriuo metu aiškiau suvokiate, kur jis eina ir kaip greitai, tuomet mažiau įsivaizduojate, kur jis yra dabar.

Mokslininkai jau buvo sužinoję, kodėl tam tikros medžiagos įkaitusios ar kitaip sužadintos skleidžia būdingų spalvų šviesą. Heizenbergas bandė paaiškinti, kodėl kiekviena iš šių spalvų pasižymi tam tikru ryškumu. Nebūtų buvę pakankamai gerai, jei jis ir kiti mokslininkai būtų tiesiog pasakę: "Na, taip jau yra". Jie buvo įsitikinę, kad šiems skirtumams ir tam, kad kiekvieno elemento mėginio ryškių linijų stiprumo santykiai visada vienodi, turi būti rimta priežastis.

Jis nė nenutuokė, kad užklups paslėptą gamtos paslaptį, kai ėmėsi ieškoti paaiškinimo, kaip paaiškinti kiekvienam elementui būdingų spalvotų linijų intensyvumą. Kvantinės mechanikos tyrimai jau buvo parodę, kodėl vandenilis turi keturias ryškias linijas toje spektro dalyje, kurią mato žmonės. Turbūt atrodė, kad kitas dalykas, kurį reikės išmokti, bus tiesiog apskaičiuoti jų ryškumą. Vandenilis atrodė akivaizdi pradžia, nes vandenilis turi tik vieną elektroną, su kuriuo reikia dirbti, ir tik keturias linijas matomoje spektro dalyje. Be abejo, turi būti rimta priežastis, kodėl jos nėra vienodai ryškios. Skirtingų spalvų neono ir kitų elementų linijų ryškumo paaiškinimas galėjo palaukti.

 

Heizenbergas pradėjo dirbti kvantinės fizikos srityje pritaikydamas klasikines elektros lygtis, kurios yra labai sudėtingos, todėl jo 1925 m. straipsnio matematiką buvo labai sunku suprasti.

Jis bandė rasti tinkamą būdą, kaip apskaičiuoti ryškių linijų intensyvumą vandenilio lempos spektre. Jis turėjo rasti susijusį dydį, vadinamą amplitude, ir padauginti amplitudę iš amplitudės (kitaip tariant, turėjo amplitudę pakelti kvadratu), kad gautų norimą intensyvumą. Jis turėjo sugalvoti, kaip išreikšti amplitudę taip, kad būtų atsižvelgta į tai, jog vandenilinės lempos spinduliuoja ne visais dažniais ir nespinduliuoja ištisiniu dažnių diapazonu toje spektro dalyje, kurią mato žmonės. Heizenbergas rado puikų naują amplitudės apskaičiavimo būdą.

Keista lygtis|lygtis, kurią Heizenbergas atrado ir naudojo vienam kvantiniam dydžiui (pvz., padėčiai) dauginti iš kito (pvz., impulso), buvo paskelbta 1925 m. liepos mėn. paskelbtame "stebuklingame Heizenbergo straipsnyje".

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

Aukščiau pateikta matematika atrodo labai sunki, tačiau ją sudaranti matematika yra daug sunkesnė ir ją labai sunku suprasti. Ji čia pateikiama tik tam, kad parodytume, kaip ji atrodė. Heizenbergo straipsnis yra istorinis orientyras. Daugelis fizikų, perskaičiusių jo straipsnį, sakė, kad negali nesutikti su jo išvadomis, bet negali suprasti jo paaiškinimo, kaip jis priėjo prie tų išvadų. Pradžios lygtys, kurias Heizenbergas naudojo, apėmė Furjė eilutes ir daugybę veiksnių. Prie pirmiau pateiktos lygties dar sugrįšime, nes ji yra savotiškas matricų užrašymo ir dauginimo receptas.

Naujosios lygtys turėjo būti tokios keistos ir neįprastos, nes Heizenbergas aprašė keistą pasaulį, kuriame kai kurie dalykai, pavyzdžiui, elektronų orbitos, lėtai neauga ir nemažėja. Naujos rūšies pokyčiai susiję su šuoliais ir dideliais tarpais tarp šuolių. Elektronai gali šokinėti tik tarp tam tikrų orbitų, o energija, įgyjama arba prarandama keičiantis orbitoms, atsiranda, kai sugeriamas reikiamos energijos fotonas arba sukuriamas naujas reikiamos energijos fotonas. Jei vandenilio atomų elektronai dažniausiai šokinėja žemyn (krenta) tarp dviejų konkrečių orbitų, tuomet tame energijos lygmenyje bus išspinduliuojama daugiau fotonų, todėl tame lygmenyje susidaranti šviesa bus intensyviausia.

Buvo sunku pritaikyti lygtis, sudarytas ištisiniams spektrams (tai, ką matote, kai saulės šviesą praleidžiate pro prizmę), spektrams, kurie turi tik kelis maksimalius dažnius, tarp kurių nieko nėra. Beveik viskas, kas jau buvo išmokta apie šviesą ir energiją, buvo daroma su dideliais objektais, pavyzdžiui, degančiomis žvakėmis ar saulėmis, o visi šie dideli objektai sukuria ištisinius spektrus. Nors su šiais įprasto dydžio daiktais buvo lengva atlikti eksperimentus, vis dėlto prireikė daug laiko, kol buvo išsiaiškinti juos valdantys fizikos dėsniai. Dabar fizikams teko susidurti su per mažais daiktais, kurie buvo per maži, kad juos būtų galima įžiūrėti, kurie nesukuria ištisinių spektrų, ir jie bandė rasti būdą, kaip iš to, ką jau žinojo, bent jau gauti užuominų, kurios padėtų rasti šių mažų ir tarpinių šviesos šaltinių dėsnius.

Pirminėse lygtyse buvo nagrinėjamas tam tikras vibruojantis kūnas, kuris sukeltų bangą, panašiai kaip vargonų nendrė sukelia tam tikro dažnio garso bangą. Taigi, buvo judėjimas pirmyn ir atgal (kaip ir nendrės vibravimas) ir skleidžiama banga, kurią galima pavaizduoti grafike kaip sinusoidę. Didžioji dalis anksčiau išaiškintų fizikos dalykų, susijusių su atomų lygmens fizika, buvo susiję su elektronų judėjimu aplink branduolius. Kai masė juda orbita, kai ji sukasi aplink kokį nors centrą, ji turi vadinamąjį "kampinį momentą". Kampinis momentas - tai būdas, kuriuo toks daiktas, kaip karuselė, nustojus ją stumti, toliau sukasi. Matematika, naudojama fazių skaičiavimams ir kampiniam momentui apskaičiuoti, yra sudėtinga. Be to, 1925 m. straipsnyje Heizenbergas nepateikė visų savo skaičiavimų, todėl net geriems matematikams gali būti sunku užpildyti tai, ko jis nepasakė.

Nors daugelis fizikų teigė negalintys suprasti įvairių matematinių veiksmų, atliktų Heizenbergo proveržio straipsnyje, viename naujausiame straipsnyje, kuriame bandoma paaiškinti, kaip Heizenbergas gavo savo rezultatą, yra dvidešimt matematikos kupinų puslapių. Net ir tą straipsnį nėra lengva suprasti. Matematika prasidėjo nuo tikrai sudėtingų dalykų ir galiausiai turėjo duoti kažką palyginti paprasto, kas parodyta šio straipsnio viršuje. Gauti paprastesnį rezultatą nebuvo lengva, ir mes nebandysime parodyti proceso, kaip nuo pasenusio visatos vaizdo pereiti prie naujosios kvantinės fizikos. Mums reikia tik tiek detalių, kad parodytume, jog beveik iškart po Heizenbergo atradimo atsivėrė iki tol niekam nematyta visatos veikimo dalis.

Heizenbergas turėjo būti labai susijaudinęs, bet kartu ir labai pavargęs, kai vėlai vakare pagaliau pasiekė proveržį ir ėmė įrodinėti sau, kad tai veiks. Beveik iš karto jis pastebėjo kažką keisto, kažką, ką laikė erzinančia maža problema, kurią galėtų kaip nors išspręsti. Tačiau paaiškėjo, kad ši maža bėda buvo didelis atradimas.

Heizenbergas siekė amplitudes dauginti iš amplitudžių, o dabar Heizenbergas turėjo gerą būdą amplitudei išreikšti, naudodamas savo naująją lygtį. Natūralu, kad jis galvojo apie daugybą ir apie tai, kaip dauginti dalykus, kurie buvo pateikti sudėtingomis lygtimis.

Heizenbergas suprato, kad, be amplitudės kvadrato, ilgainiui jis norės padauginti padėtį iš impulso arba padauginti energiją iš laiko, ir atrodė, kad bus skirtumas, jei jis pakeis tvarką šiais naujais atvejais. Heizenbergas nemanė, kad turėtų būti svarbu, ar dauginti padėtį iš impulso, ar dauginti impulsą iš padėties. Jei tai būtų buvę tik paprasti skaičiai, nebūtų kilę jokių problemų. Tačiau abu jie buvo sudėtingos lygtys, o tai, kaip gauti skaičius, kuriuos reikia įrašyti į lygtis, pasirodė esą skirtinga, priklausomai nuo to, nuo kurio kelio pradėjome. Gamtoje reikėjo išmatuoti padėtį ir tada išmatuoti momentą arba reikėjo išmatuoti momentą ir tada išmatuoti padėtį, o matematikoje vyravo ta pati bendra situacija. (Jei norite sužinoti smulkmenas, žr. angliškąjį Vikipedijos straipsnį Heisenbergo įėjimas į matricų mechaniką!) Mažyčiai, bet įkyrūs skirtumai tarp rezultatų turėjo išlikti, kad ir kaip Heizenbergas norėjo, kad jie išnyktų.

Tuo metu Heizenbergas negalėjo atsikratyti tos vienos mažos problemos, bet buvo išsekęs, todėl atidavė savo darbą tiesioginiam vadovui Maksui Bornui ir išėjo atostogų.

Maksas Bornas buvo puikus matematikas, kuris netrukus pastebėjo, kad Heizenbergo pateikta lygtis yra savotiškas matricos užrašymo receptas. Daktaras Bornas buvo vienas iš nedaugelio to meto žmonių, kurie domėjosi šia keista matematikos rūšimi, kuri daugumai žmonių atrodė nelabai tinkama. Jis žinojo, kad matricas galima dauginti, todėl visus skaičiavimus, skirtus vienam fizikos uždaviniui spręsti, galima atlikti dauginant vieną matricą iš kitos. Tiesiog gebėjimas sudėtingą procedūrą įvesti į standartinę ir priimtiną formą palengvintų darbą. Taip pat būtų lengviau ją priimti kitiems žmonėms.

Bornas buvo toks geras matematikas, kad beveik iš karto suprato, jog pakeitus abiejų matricų dauginimo tvarką gaus skirtingą rezultatą, ir rezultatai skirsis nedaug. Šis dydis būtų h/2πi. Kasdieniame gyvenime šis skirtumas būtų toks mažas, kad jo net nepastebėtume.

Dvi bangos, kurių fazės nesutampa.


Neono spektras


Visas regimasis saulės spektras. Nėra jokių spragų. Šioje diagramoje parodytas įvairių dažnių intensyvumas.


Kai tam tikros molekulės sužadinamos, jos išskiria būdingą spalvą.


Vandenilio spektras

Apie formalią neapibrėžtumo teoriją

Prireikė kelerių metų, tačiau Heizenbergui pavyko įrodyti neapibrėžtumo principą, kuris teigia, kad Δx × Δp = h/2, t. y. skaičius, kuris išplaukia iš pradinių lygčių, bet neįtraukia π ir i, kurie susiję su fazės pokyčiais. Heizenbergas paaiškino, kad savo neapibrėžtumo principą jis išvedė iš šio ankstesnio rezultato, kai 1927 m. parašė straipsnį, kuriame pristatė šią teoriją.

Užrašyta konstanta h, vadinama Planko konstanta, yra paslaptingas skaičius, kuris dažnai pasitaiko, todėl turime suprasti, kas yra šis mažytis skaičius. Skaitmenine išraiška jis paprastai nurodomas kaip 6,62607×10^-34 J s (džaulio sekundės). Taigi tai yra dydis, apimantis energiją ir laiką.

Jis buvo atrastas, kai Planckas suprato, kad tobulo spinduliuotojo (vadinamo juodojo kūno spinduliuotoju) energija sklinda tam tikro dydžio vienetais, vadinamais "kvantais" (šio žodžio vienaskaita yra "kvantinis"). Spinduliuojama energija išspinduliuojama fotonais, o fotono dažnis yra proporcingas jo skleidžiamam "smūgiui". Skirtingus matomos šviesos dažnius mes suvokiame kaip skirtingas spalvas. Violetiniame spektro gale kiekvienas fotonas turi palyginti didelį energijos kiekį; raudoname spektro gale kiekvienas fotonas turi palyginti mažą energijos kiekį. Fotono energijos kiekį galima apskaičiuoti pagal lygtį E = hν (energija lygi Planko konstantai, padaugintai iš "nu" arba dažnio).

Heizenbergo neapibrėžtumo principas Δx × Δp ≥ h sako, kad kai bandome nustatyti tam tikras skaičių poras, galime tik tiek priartėti, ir kad jei bandysime aiškiau nustatyti vieną iš jų, t. y. jei bandysime sumažinti Δx, kad geriau įsivaizduotume ko nors padėtį, turėsime gauti didesnį skaičių kitam poros skaičiui ir kad šių dviejų skaičių nuokrypis yra glaudžiai susijęs su h.

Kita fizikinių dydžių pora atitinka neapibrėžtumo priklausomybę: ΔE × Δt ≥ h, ir ši pora, be kita ko, rodo, kad, jei ieškosime tarpžvaigždinėje erdvėje, kokioje nors vietoje, kur apskritai nieko nesitikėtume rasti, ir mažinsime Δt vis arčiau ir arčiau 0, tai, norint išlaikyti lygtyje nurodytą pusiausvyrą, ΔE turi vis didėti ir didėti - ir staiga kažkas, turintis pagreitį, gali atsirasti tik tam trumpam laiko tarpui.

Kaip paaiškinti šį neapibrėžtumą (tikrumo stoką)? Kas vyksta Visatoje? Dažnai sakoma, kad sėkmingai sukurta nauja teorija gali suteikti naujos informacijos apie tiriamus reiškinius. Heizenbergas sukūrė matematinį modelį, kuris numatė teisingus vandenilio ryškiosios linijos spektro intensyvumus, tačiau neketindamas to daryti atrado, kad tam tikros fizikinių dydžių poros atskleidžia netikėtą neapibrėžtumą. Iki tol niekas neturėjo minties, kad matavimų negalima amžinai daryti vis tikslesnių ir tikslesnių. Faktas, kad jų negalima padaryti tikresnių, tikslesnių, buvo stulbinantis naujas atradimas. Daugelis žmonių nenorėjo su tuo sutikti.

Boras ir jo kolegos teigė, kad fotonai, elektronai ir kt. neturi nei padėties, nei impulso, kol nėra išmatuoti. Ši teorinė nuostata atsirado atradus neapibrėžtumą ir nebuvo tik asmeninis pasirinkimas, kuo tikėti. Boras teigė, kad mes nieko nežinome apie tokius dalykus kaip fotonas ar elektronas, kol jų nepastebime. Kad galėtume stebėti tokį mažą daiktą, turime kaip nors su juo sąveikauti. Kasdieniame gyvenime tai galima daryti, pavyzdžiui, einant šalia automobilio ir žymintis, kada jis kerta ant grindinio nubraižyto tinklelio taškus. Galbūt pats automobilio svoris nuspaudžia mažas svirtis šaligatvyje, kurios įjungia prie kiekvienos iš jų pritvirtintus laikrodžius ir fiksuoja automobilio svorį. Galiausiai turėtume aiškų įrašą, kur automobilis buvo įvairiu metu, taip pat galėtume apskaičiuoti jo judėjimo kryptį ir svorį. Tuomet bet kuriuo laikrodžio rodmeniu galėtume sužinoti ir jo padėtį, ir jo pagreitį (greitį, padaugintą iš masės). Net neįsivaizduotume, kad jėga, kurios reikia mažoms svirtelėms pajudinti, turėtų kokios nors įtakos automobilio judėjimui. Taip pat neįsivaizduotume, kad automobilis neturi jokios padėties ar trajektorijos tarp tų taškų ant grindinio, kur yra svirtys, arba kad automobilis tuo metu egzistuoja tarsi trimatėje dėmėje ir nusistovi tik tuo metu, kai nuspaudžia svirtį. Mums pažįstamas pasaulis neatskleidžia šių keistų sąveikos rūšių.

Norėdami nustatyti laivo buvimo vietą jūroje tamsiausią naktį, galėtume naudoti prožektorių, ir ši šviesa nesutrikdytų laivo padėties ar judėjimo krypties, tačiau norint nustatyti elektrono buvimo vietą naudojant šviesą, reikėtų į jį pataikyti vienu ar keliais fotonais, kurių kiekvienas turėtų pakankamai impulso, kad sutrikdytų elektrono padėtį ir trajektoriją. Norint nustatyti elektrono buvimo vietą kitomis priemonėmis, reikėtų jį sulaikyti kokiu nors fiziniu suvaržymu, kuris taip pat nutrauktų jo judėjimą pirmyn.

Norint nustatyti fotono buvimo vietą, geriausia, ką galima padaryti nenutraukiant jo judėjimo pirmyn, - priversti jį praeiti pro apskritą skylę užtvaroje. Jei žinome laiką, kada fotonas buvo išspinduliuotas (pavyzdžiui, lazeriu), ir laiką, kada fotonas pasiekia aptikimo ekraną, pavyzdžiui, skaitmeninį fotoaparatą, galima apskaičiuoti laiką, kurio prireikė tam atstumui įveikti, ir laiką, per kurį fotonas praėjo pro skylę. Tačiau tam, kad pro ją galėtų praeiti fotonas, apskritos skylės skersmuo turi būti didesnis už fotono dydį. Kuo mažesnė apskrita skylė, tuo arčiau tikslios fotono padėties sužinome, kai jis pro ją praeina. Tačiau niekada negalėsime žinoti, ar fotonas tuo metu nėra nukrypęs nuo centro. Jei skylė yra lygiai tokio pat dydžio kaip fotonas, jis pro ją nepraeis. Mažėjant skylės skersmeniui, fotono, išeinančio iš skylės, impulsas arba kryptis vis labiau ir labiau kinta.

Nielsas Boras ir jo kolegos teigė, kad mes pateksime į didelę bėdą, jei manysime, kad viskas, ką turime įrodymų tik kasdienio gyvenimo mastu, yra tiesa apie dalykus, kurie yra per maži, kad juos būtų galima pamatyti net mikroskopu. Kasdieniame gyvenime daiktai visada turi tam tikrą padėtį. Atomo masteliu neturime jokių įrodymų tokiai išvadai pagrįsti. Kasdieniame gyvenime daiktai turi konkretų laiką, kuriuo jie atsiranda. Atomo mastu neturime jokių įrodymų, patvirtinančių tokią išvadą. Kasdieniame gyvenime, jei stebime gamyklą nuo pirmos dienos naktinės pamainos iki antros dienos pamainos ir matome, kaip gatavas automobilis išvežamas į krovinių doką, nebūtų prasmės sakyti, kad neįmanoma pasakyti, ar jis buvo pristatytas per naktinę, ar per dieninę pamainą. Tačiau atominiu masteliu galime parodyti atvejų, kai vieną fotoną turime skaičiuoti kaip pagamintą dviem laikotarpiais. (Jei tai nėra pakankamai blogai, taip pat galime parodyti atvejus, kai vieną fotoną pagamina du gretimi lazeriai).

Dalis sunkumų nustatant, kas vyksta atomo mastu, yra tai, kad norėtume žinoti, kur kažkas yra ir kokia yra jo trajektorija, ir žinoti abu dalykus tuo pačiu metu, tačiau negalime vienu metu išmatuoti ir padėties, ir trajektorijos. Arba vienu metu išmatuojame fotono ar elektrono judesio momentą, o paskui, neatidėliodami daugiau nei būtina, išmatuojame jo padėtį, arba apsikeičiame vietomis ir pirmiausia išmatuojame padėtį, o paskui judesio momentą. Problema yra ta, kad, priversdami pirmąjį matavimą įgauti gana apibrėžtą formą (kaip nors jį suspausdami), padidiname neapibrėžtumą, susijusį su kitu matavimu. Jei mūsų pradiniai matavimai būtų tokie primityvūs, kad kiekviename iš jų atsirastų daug paklaidų, tada galėtume pagerinti padėtį, atlikdami kiekvieną iš jų lengvesniu prisilietimu, bet niekada negalėtume peržengti tam tikros tikslumo ribos.

Iš kasdienio gyvenimo žinome, kad bandant ką nors pasverti ant vonios kambario svarstyklių, pastatytų ant skalbyklės, kurioje vyksta sukimo ciklas, rezultatai bus netikslūs, nes svarstyklių rodyklė smarkiai svyruos. Galime išjungti skalbyklę. Tačiau norėdami atlikti labai tikslius matavimus pastebime, kad netoliese važiuojantys sunkvežimiai priverčia adatėlę virpėti, todėl svarstykles galime padėti ant ko nors, kas jas izoliuotų nuo išorinių trikdžių. Manome, kad vibracijas galime pašalinti tiek, kad rezultatai būtų tokie tikslūs, kokių norime. Niekada nepagalvojame, kad daiktas ant svarstyklių pats vibruoja arba kad jis turi neapibrėžtą pagreitį.

Remiantis neapibrėžtumo principu, atrodo, kad iš tikrųjų nėra jokios apibrėžtos padėties ir jokio apibrėžto impulso bet kokiam atominio mastelio daiktui ir kad eksperimentatoriai gali priversti daiktus būti apibrėžtus tik neapibrėžtumo principo nustatytose ribose. Boras ir jo kolegos tik teigė, kad nieko negalime sužinoti neatlikę matavimų, o atlikę matavimus galime pastūmėti dalykus aiškesnės padėties ar aiškesnio impulso link, tačiau negalime pasiekti absoliutaus apibrėžtumo ar tikrumo, kurio norėtume. Tačiau kiti šią galimybę vertino rimtai ir teigė, kad jei matematika teisinga, tai itin mažame pasaulyje negali būti apibrėžtumo ar tikrumo. Mokslo prigimtis tokia, kad matematika yra tik tikrovės modelis, ir nėra jokios garantijos, kad tai teisingas modelis.

Matematika ir praktinės pasekmės yra tokios patikimos, kad su jomis sunku nesutikti, tačiau tai, ką matematika sako apie realųjį pasaulį, sukėlė keletą skirtingų idėjų. Tarp mokslininkų, dirbusių su Nilsu Bohru Kopenhagoje, neapibrėžtumo principas buvo suprantamas kaip reiškiantis, kad elementariu lygmeniu fizinė visata neegzistuoja deterministine forma. Veikiau ji yra tikimybių arba potencialų rinkinys.

Priešingai Kopenhagos grupės matematikos istorijai, yra ir kitų istorijų, pavyzdžiui, "daugybės visatų interpretacija", kuri teigia, kad kiekvieną kartą, kai pagal kvantinę teoriją yra kelios galimos baigtys, kiekviena baigtis įvyksta atskiroje naujoje visatoje. Einšteinas teigė, kad daugybės galimų baigčių nėra, todėl egzistuoja tik viena visata ir ji yra determinuota, arba, jo žodžiais tariant, "Dievas nežaidžia kauliukais".

Jei h būtų mažiausias įmanomas energijos kiekis, pagrindinė lygtis, rodanti skirtingo dažnio fotonuose esančią energiją, nebūtų subalansuota. Ji būtų klaidinga.

Prieštaravimai neapibrėžtumo principui

Albertas Einšteinas pastebėjo, kad naujoji kvantinė mechanika reiškia, jog prieš atliekant matavimus nebuvo padėties ir impulso, ir griežtai tam paprieštaravo. Jis buvo tvirtai įsitikinęs, kad daiktai prieš juos matuojant turėjo konkrečias padėtis ir konkrečius momentus, o tai, kad matuojant vieną iš poros daiktų ir sutrukdžius galimybę tiksliai išmatuoti kitą daiktą, negalima teigti, kad prieš tai nebuvo nė vieno iš jų. Jis ir du jo kolegos parašė tai, kas tapo žinoma kaip "EPR dokumentas". Šiame straipsnyje teigiama, kad turi būti charakteristikos, kurios lemia padėtį ir pagreitį, ir kad, jei galėtume jas pamatyti arba jei galėtume gauti informacijos apie jas, tada galėtume matematiškai pažinti ir nuspėti padėtį ir pagreitį. Ilgą laiką žmonės manė, kad neįmanoma įrodyti ar paneigti to, kas Einšteinui buvo tikėjimo straipsnis. Šis ginčas buvo labai produktyvus, nes paskatino visus šiuolaikinius susietumo pasiekimus.

Matematiškai įrodyta, kad Einšteinas klydo. 1964 m. Džonas Stiuartas Belas (John Stewart Bell) sukūrė matematinį metodą, leidžiantį atskirti dviejų dalelių, turinčių determinuotas būsenas, kurios yra nežinomos tik dviem jas tiriantiems asmenims, ir dviejų dalelių, turinčių susietas būsenas, kurios yra neapibrėžtos arba neaiškios, kol nėra išmatuotos, elgesį. Jo metodas parodo, kad tikimybės gauti tam tikrus rezultatus yra skirtingos esant dviem skirtingoms prielaidoms. Jo darbas vadinamas Bello teorema arba Bello nelygybe. Eksperimentai parodė, kad gamta elgiasi taip, kaip ją aprašo Bellas.

Kitas kelias į neapibrėžtumą

Pradinės Heizenbergo neapibrėžtumo principo diskusijos priklausė nuo modelio, kuriame neatsižvelgta į tai, kad materijos dalelės, tokios kaip elektronai, protonai ir kt., turi bangos ilgį. 1926 m. Luji de Brolis (Louis de Broglie) parodė, kad visi daiktai, ne tik fotonai, turi savo dažnį. Daiktai, kaip ir fotonai, turi banginę ir dalelių prigimtį. Jei pabandytume tokio daikto kaip protonas bangą padaryti siauresnę ir aukštesnę, jo padėtis taptų aiškesnė, bet tada momentas taptų ne toks aiškus. Jei bandytume bangos aprašymo dalį momentą padaryti aiškesnę, t. y. padaryti taip, kad jis liktų siauresniame verčių intervale, tada bangos viršūnė išsiplėstų ir jos padėtis taptų mažiau apibrėžta.

Kvantinėje mechanikoje banga, kuri yra fotono aprašymo dalis, nėra tas pats dalykas, kaip banga vandenyno paviršiuje arba suslėgto ir reto oro sritys, sudarančios garso bangas. Vietoj to šios bangos turi viršūnes arba didelės amplitudės sritis, kurios susijusios su tikimybe ką nors rasti tame erdvės ir laiko taške. Tiksliau tariant, būtent amplitudės kvadratas parodo tikimybę, kad koks nors reiškinys pasirodys.

Fotonui taikoma banga gali būti gryna sinusoidė. Tokiu atveju kiekvienos viršūnės reikšmės kvadratas nusakytų tikimybę, kad tame taške bus pastebėtas fotonas. Kadangi sinusinių bangų amplitudės visur vienodos, tikimybė rasti fotoną kiekvienoje iš jų būtų vienoda. Taigi, praktiškai kalbant, žinant vieno iš šių fotonų bangą, nebūtų galima sužinoti, kur jo ieškoti. Kita vertus, fotono impulsas matematiškai susijęs su jo bangos amplitude. Kadangi šiuo atveju turime gryną sinusinę bangą, kiekvieno bangos ciklo amplitudė yra vienoda, todėl su šia banga susijusi tik viena impulso vertė. Nežinotume, kur pataikys fotonas, bet tiksliai žinotume, kaip stipriai jis pataikys.

Šviesos spinduliuose, kurie susitelkia į tam tikrą aptikimo ekrano tašką, su fotonais susijusios bangos nėra grynos sinusoidės. Tai bangos, kurių amplitudė viename taške yra didelė, o abipus tos didžiausios viršūnės yra daug mažesnės amplitudės. Matematiškai tokią bangą galima išanalizuoti į keletą skirtingų sinusinių bangų, kurių bangos ilgis skiriasi. Šį procesą šiek tiek lengviau įsivaizduoti atvirkščiai - pažvelgus į pradinę vieno dažnio sinusoidę, prie kurios pridedama antroji kitokio bangos ilgio sinusoidė, tada trečioji, ketvirtoji ir t. t. Rezultatas bus sudėtinga banga, turinti vieną aukštą viršūnę ir daugybę skirtingų bangų ilgių, taigi ir skirtingų momentų bangų. Tokiu atveju tikimybė, kad fotonas pasirodys tam tikrame taške, yra labai didelė, tačiau jo perduodamas impulsas gali pasirodyti susijęs su bet kurios iš sudedamųjų bangų bangos ilgiu. Kitaip tariant, p = ħ/λ reikšmė nebėra viena reikšmė, nes reikia atsižvelgti į visus surinktų "skirtingo bangos ilgio bangų" ilgius.

Simuliacija parodo, kaip matematiškai modeliuoti dalelės vietos aštrėjimą: Ant pradinės sinusinės bangos uždėkite daugybę skirtingų bangų formų. Centras suformuos vis aukštesnę viršūnę, o likusių viršūnių skaičius padidės, bet jų aukštis sumažės, nes jos interferuos viena su kita. Taigi galiausiai superpozicijoje yra daug skirtingų bangų, kurių kiekviena turi skirtingą bangos ilgį ir (pagal p = ħ/λ) skirtingą impulsą, bet tik vieną labai aukštą viršūnę, kuri vis didėja ir siaurėja ir suteikia mums kažką vis arčiau ir arčiau apibrėžtos padėties.

Kad pagreitis taptų vis aiškesnis, turėtume pašalinti vis daugiau sinusoidžių, kol liktų tik paprasta sinusoidė. Tokiu būdu palaipsniui mažintume centrinės viršūnės aukštį ir palaipsniui didintume konkuruojančių vietų, kuriose galima rasti dalelę, aukščius.

Taigi, kai pradedame kurti subatominių dalelių banginį vaizdą, paprastai visada susiduriame su atvejais, kai centrinės viršūnės yra palyginti didelės, o sudedamųjų bangų ilgiai palyginti dideli. Tokiomis aplinkybėmis niekada nebus galima nuspėti tikslios padėties ar tikslaus impulso. Jei matematinis modelis tiksliai atspindi realųjį pasaulį, tai joks fotonas ar kita subatominė dalelė neturi nei tikslios padėties, nei tikslaus impulso. Matuodami tokią dalelę galime pasirinkti metodą, kuris dar labiau suspaudžia smailę ir ją susiaurina, arba galime pasirinkti metodą, kuris smailę sumažina ir išlygina sudedamųjų bangų ilgius. Priklausomai nuo to, ką matuojame ir kaip matuojame, galime pasiekti, kad mūsų buvimo vieta būtų tikslesnė, arba susiaurinti impulso diapazoną. Planuodami eksperimentą galime pasirūpinti, kad išvengtume įvairių aparato pajudinimo būdų, tačiau negalime atsikratyti fakto, kad iš pradžių nebuvo nieko visiškai aiškaus.

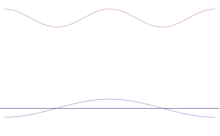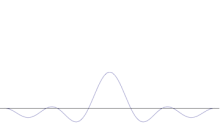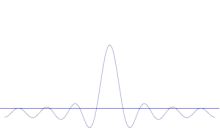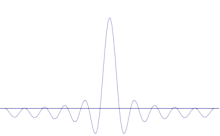
Kelių plokščių bangų superpozicija. Sudėjus daug bangų, bangų paketas tampa vis labiau lokalizuotas. Furjė transformacija yra matematinė operacija, kuria bangų paketas išskaidomas į atskiras plokštumines bangas. Atkreipkite dėmesį, kad čia pavaizduotos bangos tik iliustraciniais tikslais yra realios, o kvantinėje mechanikoje banginė funkcija paprastai yra kompleksinė.

Kultūros įtaka

Didžiausią įtaką Heizenbergo neapibrėžtumo principas padarė argumentams apie valios laisvę. Remiantis klasikinės fizikos teorijomis, galima teigti, kad priežasties ir pasekmės dėsniai yra nenumaldomi ir kad, visatai prasidėjus tam tikru būdu, iš tos pradinės būsenos galima apskaičiuoti visų ateityje įvyksiančių materijos ir energijos sąveikų. Kadangi viskas yra absoliučiai to, kas buvo prieš tai, rezultatas, jie teigė, kad kiekvienas žmogaus sprendimas ir kiekviena situacija, į kurią jis patenka, buvo iš anksto nulemta nuo laiko pradžios. Tuomet mes neturime jokio pasirinkimo, ką daryti.

Žmonės, tikintys valios laisve, teigia, kad kvantinės mechanikos dėsniai nenumato, kas nutiks, o tik numato, kas labiau ir kas mažiau tikėtina. Todėl kiekvienas veiksmas yra atsitiktinių "monetos metimų" serijos rezultatas, ir joks sprendimas negali būti susietas su būtinų išankstinių sąlygų rinkiniu.

Išsireiškimai "kvantinis šuolis" ir "kvantinis šuolis" tapo įprastais kalbėjimo apie dalykus būdais. Paprastai žmonės nori apibūdinti ką nors, kas susiję su didžiuliu pokyčiu, įvykstančiu per trumpą laiką. Iš tikrųjų šis terminas taikomas elektronui atome, kai jis sugeria iš išorės atėjusį fotoną ir iš vienos orbitos aplink atomo branduolį peršoka į aukštesnę, arba kai jis išspinduliuoja fotoną ir iš aukštesnės orbitos nukrenta į žemesnę. Neilsas Boras ir jo kolegos manė, kad elektronas nejuda iš vienos orbitos į kitą, o išnyksta iš vienos orbitos ir akimirksniu atsiranda kitoje. Taigi kvantinis šuolis iš tiesų yra ne koks nors žemę sukrečiantis pokytis, o staigus nedidelis pokytis iš vienos srities į kitą.

Kai žmonės matuoja kokį nors procesą subatominiu mastu ir pasireiškia neapibrėžtumo principas, galima sakyti, kad žmogaus veiksmai turėjo įtakos matuojamam dalykui. Atliekant matavimą, kurio tikslas - gauti tikslią informaciją apie dalelės buvimo vietą, neišvengiamai bus daromas poveikis jos impulsui, ir kad ir kas būtų daroma, kad tas impulsas būtų išmatuotas kuo greičiau po to, kai buvo išmatuota dalelės padėtis, tikimybė, koks impulsas bus nustatytas, negali nepasikeisti. Taigi neapibrėžtumo principu galima paaiškinti kai kurių rūšių tyrėjų sukeliamus trukdžius, kurie daro įtaką eksperimento ar stebėjimo rezultatams. Tačiau ne visi stebėtojų poveikiai yra susiję su kvantiniais efektais ar neapibrėžtumo principu. Likusieji yra "stebėtojo efektai", bet ne kvantinio neapibrėžtumo efektai.

Stebėtojų poveikis apima įvairius dalykus, kurie veikia mums įprastu žmogiškuoju įvykių masteliu. Jei antropologas bando susidaryti aiškų vaizdą apie gyvenimą primityvioje visuomenėje, bet jo buvimas kelia nerimą bendruomenėje, kurioje jis lankosi, tai atlikti stebėjimai gali būti labai klaidinantys. Tačiau nė viena iš atitinkamų sąveikų nevyksta kvantinės mechanikos ar neapibrėžtumo principo aprašomu lygmeniu.

Kartais žodis "kvantinis" vartojamas reklamos tikslais, siekiant nurodyti kažką naujo ir galingo. Pavyzdžiui, mažų benzininių variklių gamintoja "Briggs and Stratton" turi keturių cilindrų mažos galios variklių liniją, skirtą benzininėms vejapjovėms ir panašiems sodo įrankiams, kurią vadina "Quantum".

Daugiau skaitymo

• Kvantinės teorijos pristatymas, p. 115 ir 158

J.P. McEvoy ir Oscar Zarate