Tikimybė
Tikimybė yra taikomosios matematikos dalis. Ji susijusi su atsitiktinumais, t. y. su dalykais, kurie gali atsitikti arba neatsitikti.
Pavyzdžiui, pasitelkę tikimybę galite parodyti, kad, jei monetą išmesite į orą ir leisite jai nusileisti, pusę laiko ji nusileis viena puse į viršų, o pusę laiko - kita puse į viršų. Ant daugelio monetų vienoje pusėje pavaizduotas žymaus žmogaus veidas, o kitoje pusėje - kas nors kita. Dažnai žmonės tą pusę, kurioje pavaizduotas veidas, vadina galva, o kitą - uodega.
Įvykio tikimybė (p) visada yra nuo nulio (neįmanoma) iki vieneto (neabejotina).
Jei metame kauliuką (daugiskaita: kauliukai), tikimybė, kad jis kris ant 1, yra 1/6 (taip yra todėl, kad ant kauliuko yra 6 skaičiai). Taip pat tikimybė, kad kris 2, yra 1/6. Taip yra todėl, kad gali kristi 1, 2, 3, 4, 5 arba 6. Tikimybė, kad kris bet kuris skaičius tarp 1 ir 6, yra 1. Kiekvieną kartą metant kauliuką, jis visada kris ant skaičiaus tarp 1 ir 6.
Tikimybę galima nustatyti pasitelkiant matematiką. Pavyzdžiui, jei metate šešis kauliukus, tikimybė, kad gausite skaičių, didesnį nei dešimt, nėra akivaizdi, tačiau ją galima nustatyti pasitelkus matematiką ir gamtos mokslus.
Vienas iš įdomiausių dalykų, susijusių su atsitiktinumu, yra tai, kad norėdami nustatyti tikimybę, jog du dalykai įvyks abu kartu, turite padauginti jų tikimybes. Pavyzdžiui, tarkime, kad norite sužinoti tikimybę, jog išmesite du kauliukus ir gausite tam tikrą kombinaciją (tai gali būti dvi šešetės arba 3 ir 5, tiesiog bet kurios dvi kombinacijos). Galimybė gauti 3 yra viena iš šešių (⅙), o galimybė gauti 5 taip pat yra viena iš šešių, taigi tikimybė gauti 3 ir 5 yra ⅙×⅙=⅟36. Jei šį skaičių išreikštume kaip kažkur tarp 0 ir 1, jis būtų lygus 0,027...7, o tai yra gana mažai. Galimybė gauti 3, tada 5, o tada 2 būtų ⅙×⅙×⅙×⅙=⅟216 arba 0,00463, o tai yra daug mažesnė tikimybė.
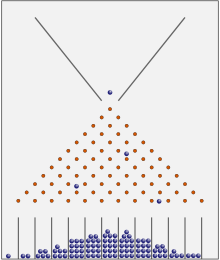
Pupelių mašinoje arba Galtono dėžutėje dauguma kamuoliukų atsiduria arti centro. Ilgainiui jie pasiskirstys normaliai
Tikimybės idėjos
Tokie žmonės kaip Jacobas Bernoulli, Pierre'as-Simonas Laplace'as ar Christiaanas Huygensas vartojo žodį tikimybė, kaip aprašyta pirmiau. Kiti žmonės galvojo apie dažnius; ten tikimybės sąvoka paprastai vadinama dažnio tikimybe.
Susiję puslapiai
- Matematikos temų sąrašas
- Tikimybių teorija
Klausimai ir atsakymai
K: Kas yra tikimybė?
Atsakymas: Tikimybė yra taikomosios matematikos dalis, nagrinėjanti dalykus, kurie gali atsitikti arba neatsitikti.
K: Kaip galima išreikšti tikimybę?
A: Tikimybė gali būti išreikšta skaičiumi nuo nulio (neįmanoma) iki vieneto (neabejotina).
K: Koks yra tikimybės naudojimo pavyzdys?
Atsakymas: Tikimybės naudojimo pavyzdys yra toks: išmesdami monetą į orą ir leisdami jai nusileisti, pusę laiko ji nusileis viena puse į viršų, o kitą pusę laiko - kita puse į viršų.
K: Kaip apskaičiuoti tikimybę, kad metant du kauliukus gausime tam tikrą kombinaciją?
Atsakymas: Norėdami apskaičiuoti tikimybę, kad metant du kauliukus gausime tam tikrą kombinaciją, turėtumėte padauginti abi jų tikimybes. Pavyzdžiui, jei norėtumėte sužinoti tikimybę, kad gausime 3, o paskui 5, tai būtų 1/6 x 1/6 = 1/36.
K: Ką reiškia "uodegos", kai kalbama apie monetas?
A: Kai kalbame apie monetas, "uodega" reiškia tą pusę, ant kurios nėra paveikslėlio.
K: Kokia tikimybė, kad, metant šešis kauliukus, gausime skaičių, didesnį nei dešimt? Atsakymas: Tikimybę, kad išmesdami šešis kauliukus gausime skaičių, didesnį nei dešimt, galima apskaičiuoti pasitelkus matematiką ir mokslą, tačiau ji nėra akivaizdi.
K: Kas atsitinka, kai dvi tikimybes padauginame kartu?
Atsakymas: Kai padauginate dvi tikimybes kartu, apskaičiuojate tikimybę, kad abu dalykai įvyks vienu metu.
