Minkovskio erdvėlaikis: apibrėžimas, metrinė signatūra ir reikšmė

Sužinokite, kas yra Minkovskio erdvėlaikis, jo metrinė signatūra (-+++) ir reikšmė specialiajame reliatyvume — aiškiai, glaustai ir suprantamai.

Autorius: Leandro Alegsa

02-11-2025 15:08

Minkovskio erdvėlaikis specialiajame reliatyvumo teorijoje yra Hermano Minkovskio sukurtas keturmatis daugialypis. Jis turi keturis matmenis: tris erdvės matmenis (x, y, z) ir vieną laiko matmenį. Minkovskio erdvėlaikis turi metrinę signatūrą (-+++) ir aprašo plokščią paviršių, kai nėra masės. Šiame straipsnyje įprasta Minkovskio erdvėlaikį vadinti tiesiog erdvėlaikiu.

Tačiau Minkovskio erdvėlaikis taikomas tik specialiajame reliatyvumo teorijoje. Bendrajame reliatyvume gravitacijos poveikiui ir pagreitintam judėjimui aprašyti naudojama išlenkto erdvėlaikio sąvoka.

Metrinė signatūra ir metrinis tenzorius

Minkovskio erdvėlaikio pagrindą sudaro metrinė struktūra, kuri leidžia apskaičiuoti atstumus ir laiko intervalus tarp įvykių. Linijinis elementas (intervalas) dažnai rašomas kaip

ds² = -c²dt² + dx² + dy² + dz²,

kur c yra šviesos greitis, o dažnai patogu naudoti vienetus, kur c = 1. Atitinkamas metrinis tenzorius dažnai žymimas η_μν ir matriciniu pavidalu (koordinatėse t, x, y, z) turi elementus diag(-1, 1, 1, 1). Tai atitinka signatūrą (-+++). Kai kurie autoriai naudoja priešingą konvenciją (+---); abi konvencijos yra ekvivalentinės, tik reiškiniai užrašomi su atitinkamais ženklais.

Intervalas ir jo fizinė reikšmė

Intervalas ds² yra invariantas prieš Lorenco transformacijas — jis turi tą pačią reikšmę visiems inerciniams stebėtojams. Pagal ds² klasifikuojame skirtumus tarp įvykių:

Timelike (laikinis): ds² < 0. Tarp tokių įvykių gali perduoti informacija arba dalyvis gali judėti iš vieno įvykio į kitą lėčiau už šviesą. Egzistuoja savas laikas τ, susijęs su intervale: ds² = -c² dτ².
Lightlike (šviesinis) arba null: ds² = 0. Tai yra šviesos arba kitų masės neturinčių dalelių trajektorijos (šviesos kūgis).
Spacelike (erdvinis): ds² > 0. Tarp tokių įvykių negali būti priežastinio ryšio (informacija negali perduoti greičiau už šviesą).

Šviesos kūgis ir priežastis

Šviesos kūgis (light cone) centre turi konkretų įvykį; įvykiai viduje laikinio kūgio yra galimi priežastiniai pasekmės (gali būti priežastinis ryšys), o įvykiai už kūgio ribų — ne. Tai užtikrina priežastingumo struktūrą specialiajame reliatyvume: negalima siųsti signalų ar sukelti pasekmių prieš priežastį.

Geometrija ir judėjimo trajektorijos

Minkovskio erdvėlaikis yra plokščias: kurvatura yra lygi nuliui, todėl geodezinės linijos — tiesės. Inerciniai stebėtojai juda pagal tiesias linijas laiko-rumens (worldlines) diagramoje. Lorenco transformacijos yra tokios linijinės transformacijos, kurios palieka intervalą invariantišką ir jungia skirtingus inercinius stebėtojus.

Ryšys su bendrąja reliatyvumo teorija

Nors Minkovskio erdvėlaikis puikiai tinka be gravitacijos aprašymui, bendrajame reliatyvume energįs ir masės buvimas iškreipia erdvėlaikį — metrinė struktūra tampa priklausoma nuo koordinatų ir turi net nulį ar skirtingą kurvaturą. Tokiu atveju vietoj Minkovskio plokščio erdvėlaikio naudojama išlenktų erdvėlaikių geometrija, kurią aprašo Einsteino lygtis.

Istorinė pastaba

H. Minkovskio idėja sujungti erdvę ir laiką į vieną keturmatį koncepciją padėjo aiškiai suvokti specialiojo reliatyvumo principus ir paruošė kelią geometriniam požiūriui į gravitaciją, kuris vėliau tapo bendrojo reliatyvumo pagrindu.

Santrauka: Minkovskio erdvėlaikis — tai plokščias keturmatės geometrijos modelis su signatūra (-+++), kuriame intervalas ds² yra invariantiškas ir lemia priežastingumo struktūrą, šviesos kūgio formą bei judėjimo galimybes specialiajame reliatyvume. Bendrajame reliatyvume šią idėją išplečia erdvėlaikio išlinkimas dėl masės ir energijos.

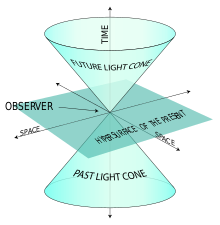
Šviesos kūgio pavyzdys.

Apibrėžimas (-ai)

Matematinis

Erdvėlaikį galima įsivaizduoti kaip keturmatę koordinačių sistemą, kurios ašys yra duotos

( c t , x , y , z ) {\displaystyle (ct,x,y,z)} $(ct,x,y,z)$

Jie taip pat gali būti žymimi

( x 1 , x 2 , x 3 , x 4 ) {\displaystyle (x_{1},x_{2},x_{3},x_{4})} $(x_{1},x_{2},x_{3},x_{4})$

Kur x 1 {\displaystyle x_{1}} $x_{1}$ reiškia c t {\displaystyle ct} $ct$ . Laikas matuojamas šviesos greičio, padauginto iš laiko koordinatės, vienetais todėl, kad laiko vienetai sutaptų su erdvės vienetais. Erdvėlaikis turi lanko ilgio diferencialą, kurį nusako

d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}+dz^{2}}} $ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}$

Tai reiškia, kad erdvėlaikis turi metrinį tenzorių, kurį sudaro

g u v = [ - 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 ] {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0&0\0&1&0&0&0\0&0&0&1&0\0&0&0&0&0&0&1\end{bmatrix}}}} $g_{uv}={\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}$

Kaip jau minėta, erdvėlaikis visur yra plokščias; tam tikra prasme jį galima laikyti plokštuma.

Paprastas

Erdvėlaikį galima laikyti "arena", kurioje vyksta visi visatos įvykiai. Viskas, ko reikia erdvėlaikio taškui apibrėžti, yra tam tikras laikas ir tipiška erdvinė orientacija. Sunku (beveik neįmanoma) įsivaizduoti keturis matmenis, tačiau galima sukurti tam tikrą analogiją, naudojant toliau pateiktą metodą.

Erdvėlaikio diagramos

Hermanas Minkovskis įvedė tam tikrą metodą, skirtą koordinačių sistemoms Minkovskio erdvėlaikyje atvaizduoti. Kaip matyti dešinėje, skirtingos koordinačių sistemos nesutaria dėl objekto erdvinės orientacijos ir (arba) padėties laike. Kaip matote iš diagramos, yra tik viena erdvinė ašis (x ašis) ir viena laiko ašis (ct ašis). Jei reikia, galima įvesti papildomą erdvinį matmenį (y ašis); deja, tai yra matmenų skaičiaus riba: keturių matmenų grafikų sudaryti neįmanoma. Minkovskio erdvėlaikio grafikų sudarymo taisyklė yra tokia:

1) Kampas tarp x ašies ir x'-ašio nustatomas pagal formulę t a n ( α ) = v c {\displaystyle tan(\alpha )={\frac {v}{c}}} $tan(\alpha )={\frac {v}{c}}$ kur v yra objekto greitis.

2) Šviesos greitis erdvėlaikyje visada sudaro 45 laipsnių kampą su bet kuria ašimi.

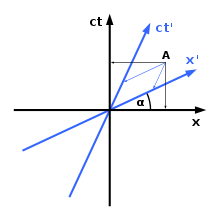
Pagal reliatyvumo teoriją abu stebėtojai įvykį A priskiria skirtingiems laikams.

Erdvėlaikis bendrajame reliatyvume

Bendrojoje reliatyvumo teorijoje Einšteinas naudojo lygtį

R u v - 1 2 g u v R = 8 π T u v {\displaystyle R_{uv}-{\frac {1}{2}}g_{uv}R=8\pi T_{uv}} $R_{uv}-{\frac {1}{2}}g_{uv}R=8\pi T_{uv}$

Tam, kad erdvėlaikis iš tikrųjų galėtų išlinkti; dėl to atsiranda gravitacijos poveikis.

Susiję puslapiai

Erdvėlaikis
Specialusis reliatyvumas
Bendrasis reliatyvumas

Valdžios institucijų kontrolė

BNF: cb11979629v (duomenys)
GND: 4293944-6

Klausimai ir atsakymai

K: Kas yra Minkovskio erdvėlaikis?

A: Minkovskio erdvėlaikis - tai Hermano Minkovskio sukurtas keturmatis daugiamatis. Jame yra trys erdvės matmenys (x, y, z) ir vienas laiko matmuo.

K: Kokia yra Minkovskio erdvėlaikio metrinė signatūra?

A: Minkovskio erdvėlaikio metrinė paraštė yra (-+++).

K: Kaip Minkovskio erdvėlaikis apibūdina plokščią paviršių?

A: Kai nėra masės, Minkovskio erdvėlaikis aprašo plokščią paviršių.

K: Ar Minkovskio erdvėlaikis taikomas bendrajam reliatyvumui?

Atsakymas: Ne, Minkovskio erdvėlaikis taikomas tik specialiajame reliatyvume. Bendrajame reliatyvume gravitacijos poveikiui ir pagreitintam judėjimui aprašyti naudojama išlenkto erdvėlaikio sąvoka.

K: Kiek matmenų turi Minkovskio erdvėlaikis?

Atsakymas: Minkovskio erdvėlaikis turi keturis matmenis - tris erdvės matmenis (x, y, z) ir vieną laiko matmenį.

K: Kas sukūrė Minkovsi erdvėlaikio sąvoką?

A: Hermanas Minkovskis sukūrė MInkovskio erdvėlaikio sąvoką.

Ieškoti