Nomograma (nomografija): apibrėžimas, veikimo principas ir istorija
Nomograma (nomografija): supraskite apibrėžimą, veikimo principą ir istoriją — nuo d'Ocagne išradimo iki praktinių grafinių skaičiavimų.
Nomograma, lyginamoji diagrama arba abaque — tai skaičiavimams skirta diagrama. Tai dvimatė grafinė priemonė, kurioje pateikiamas matematinės funkcijos arba lygčių ryšys taip, kad skaičiavimas atliekamas mechaniškai arba vizualiai, be tradicinių aritmetinių skaičiavimų.
Nomografijos sritį 1884 m. išrado prancūzų inžinierius Philbert Maurice d'Ocagne (1862–1938). Daugelį metų nomogramos buvo plačiai naudojamos inžinerijoje, hidraulikoje, chemijoje, meteorologijoje ir medicinoje — visur, kur reikėjo greitai ir patikimai apskaičiuoti sudėtingas formules arba parinkti parametrus be skaitmeninių priemonių. Vietoj standartinių Dekarto koordinačių dažnai naudojama d'Ocagne'o išrasta lygiagrečiųjų koordinačių sistema, kuri leidžia skales išdėstyti taip, kad tiesė, sujungusi žinomas reikšmes, kertų nežinomą skalę reikiamoje vietoje.
Veikimo principas
Nomogramą sudaro n skalų rinkinys — po vieną skalę kiekvienam lygties kintamajam arba kiekvienam funkcijos nariu. Jei žinomos n−1 kintamųjų reikšmės, nežinomo kintamojo reikšmę galima rasti nubrėžus arba virtualiai praplečiant tiesią liniją per žinomas reikšmes ir perskaitant sprendimą toje skalėje, kur ji kerta. Tokia nubrėžta arba įsivaizduojama tiesė vadinama indekso linija arba izopletu.
Nomogramos dažniausiai projektuojamos taip, kad du ar trys žinomi parametrai nustato trečią ar ketvirtą parametrą. Daugeliui naudingų funkcinių ryšių galima rasti transformaciją (pvz., logaritminę), kuri paverčia sudėtingą santykį į sumą ar linijinį ryšį — tada sprendimas gaunamas paprastu linijų sujungimu.
Konstrukcijos tipai
- Tiesinės (paralelinės) skalių nomogramos: skalės išdėstytos paraleliai; paprastos lygtims, kurios gali būti linijiškai sukonstruojamos arba log-transformuotos.
- Trikampės (arba ternarinės): trijų skalų išdėstymas trikampio viršūnėse, naudingas lygčių sistemoms su trimis kintamaisiais.
- Apskritiminės nomogramos: skalės išdėstytos ratu; naudojamos, kai reikia daug iteracijų arba patogesnio kampinio matavimo.
- Sudėtinės arba hibridinės: kombinuoja kelis tipų elementus, kad būtų patogiau vaizduoti sudėtingesnes funkcijas.
Pavyzdys (kaip tai veikia)
Paprastas pavyzdys — daugybos operacija. Padarius logaritminę transformaciją, lygtis A × B = C virsta logA + logB = logC. Tada ant trijų paralelinių logaritminių skalų galima taip išdėstyti žymes, kad tiesė per logA ir logB kertų logC ties teisinga verte. Tokiu būdu gaunamas rezultatas paprastu vizualiniu veiksmu be rankinių skaičiavimų.
Pritaikymas
- Inžinerija: hidrauliniai skaičiavimai, vamzdynų apkrova, konstrukcijų stiprumas.
- Medicina: dozių parinkimas, biocheminių santykių greitas vertinimas.
- Mokslas: meteorologija, farmacijos formulės, laboratoriniai skaičiavimai.
- Transportas ir aviacijos planavimas: greičio-degalų-svorio santykiai, kai reikia greitų sprendimų.
- Pramonė ir energetika: srauto, slėgio ir galios ryšiai.
Privalumai ir trūkumai
- Privalumai: greitis (sprendimas per sekundes), nereikia skaitmeninių priemonių, paprastas naudoti mokant ar lauko sąlygomis, aiškus vizualinis ryšys tarp parametrų.
- Trūkumai: ribota tikslumas (priklauso nuo skalių smulkumo ir žmogaus nubrėžimo tikslumo), ne visuomet tinkama labai sudėtingoms funkcijoms be transformacijų, sunku atlikti automatizuotą iteracinį sprendimą be skaitmeninių priemonių.
Moderni raida
Nors skaitmeniniai skaičiuotuvai ir kompiuterinės programos sumažino poreikį naudoti popierines nomogramas, jos vis dar aktualios kaip mokymo priemonė, greito sprendimo įrankis ir vizualizavimo metodas. Šiuolaikiniai įrankiai leidžia generuoti nomogramas automatiškai (pvz., su Python, Octave arba specializuota programine įranga), spausti aukštos kokybės schemą ar pateikti interaktyvias versijas planšetėms ir programėlėms.
Išvados
Nomograma — tai praktinis ir elegantiškas grafinių skaičiavimų būdas, ypač naudingas ten, kur reikia greitai gauti sprendimą be skaitmeninio skaičiavimo arba norint aiškiai pavaizduoti parametrų priklausomybes. Ji remiasi tinkamu skalių parinkimu ir dažnai naudoja transformacijas (pvz., logaritmus), kad sudėtingus ryšius paverstų linijiniais ir taip leistų spręsti tiesiųjų sankirtų pagalba.
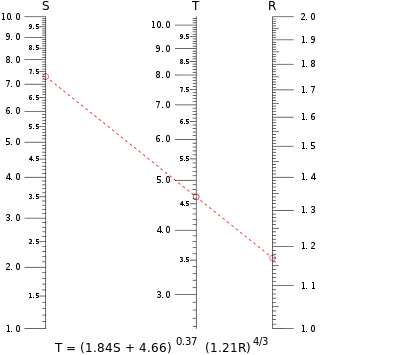
Tipiška lygiagretaus mastelio nomograma. Šiame pavyzdyje apskaičiuojama T vertė, kai į lygtį įrašoma S = 7,30 ir R = 1,17. Izopletė kerta T skalę ties 4,65.
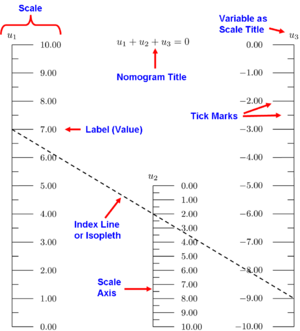
Lygiagretaus mastelio nomogramos sudedamosios dalys
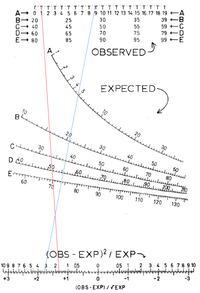
Chi kvadrato pasiskirstymo nomograma
Naudoti
Nomogramos buvo plačiai naudojamos apie 75 metus. Jos leido greitai ir tiksliai atlikti skaičiavimus iki kišeninių skaičiuotuvų eros. Nomogramos rezultatai gaunami greitai ir patikimai nubrėžus vieną ar kelias linijas. Naudotojui nereikia mokėti spręsti algebrinių lygčių, ieškoti duomenų lentelėse, naudotis slankmačiu ar įrašyti skaičių į lygtis, kad gautų rezultatus. Naudotojui net nereikia žinoti pagrindinės lygties, kurią vaizduoja nomograma.
Nomogramos yra sukurtos atsižvelgiant į srities žinias. Pavyzdžiui, norėdamas sukurti didesnes nomogramas, kad jos būtų tikslesnės, nomografas paprastai įtraukia tik tuos skalės intervalus, kurie yra pagrįsti ir svarbūs sprendžiant problemą. Daugelyje nomogramų yra ir kitų naudingų žymėjimų, pavyzdžiui, nuorodų etikečių ir spalvotų regionų. Visa tai naudotojui suteikia naudingų orientyrų.
Kaip ir slankmatis, nomograma yra grafinis analoginis skaičiavimo prietaisas. Kaip ir slankmačio, jo tikslumą riboja tikslumas, kuriuo galima nubrėžti, atkurti, peržiūrėti ir suderinti fizines žymes.Slankmatis yra bendrosios paskirties skaičiuotuvas, o nomograma skirta konkretiems skaičiavimams atlikti. Nomogramos vis tiek gali būti naudojamos atsakymui, gautam atlikus kitą, tikslesnį, bet galbūt klaidingą skaičiavimą, patikrinti.
Klausimai ir atsakymai
K: Kas yra nomograma?
A: Nomograma - tai skaičiavimams naudojamas grafikas, kuriame pateikiamas matematinės funkcijos skaičiavimas.
K: Kas išrado nomografijos sritį?
A: Nomografijos sritį 1884 m. išrado prancūzų inžinierius Philbert Maurice d'Ocagne.
K: Koks buvo nomogramų tikslas?
A. Nomogramos daugelį metų buvo naudojamos inžinieriams, kad jie galėtų greitai grafiškai apskaičiuoti sudėtingas formules.
K: Kiek skalių sudaro nomogramą?
A: Nomogramą sudaro n skalių rinkinys, po vieną kiekvienam lygties kintamajam.
K: Kaip naudojant nomogramą galima rasti nežinomo kintamojo vertę?
A: Žinant n-1 kintamųjų vertes, nežinomojo kintamojo vertę galima rasti tiesia linija perbraukus žinomus dydžius skalėse ir nežinomąją vertę nuskaičius ten, kur ji kerta to kintamojo skalę.
Klausimas: Kaip vadinama virtuali arba tiesiakalbiu nubrėžta linija?
Atsakymas: Tiesiakalbio sukurta virtuali arba nubrėžta linija vadinama indekso linija arba izopletu.
K: Kokia koordinačių sistema naudojama nomogramose?
A: Nomogramose naudojama d'Ocagne'o išrasta lygiagrečiųjų koordinačių sistema, o ne standartinės Dekarto koordinatės.
Ieškoti