Dešiniosios rankos taisyklė: vektorių kryžminės sandaugos paaiškinimas
Sužinokite dešiniosios rankos taisyklę: aiškus vektorių kryžminės sandaugos paaiškinimas su žingsniniu pirštų metodu, pavyzdžiais ir praktiniais patarimais.
Dešiniosios rankos taisyklė yra vektorių matematikos konvencija. Ji padeda prisiminti kryptį, kai vektoriai dauginami kryžminiu būdu.
- Pradėkite uždarydami dešinę ranką ir ištieskite rodomąjį pirštą.
- Iškelkite nykštį tiesiai į viršų, tarsi darytumėte ginklo ženklą.
- Jei "ginklą" nukreipiate tiesiai į priekį, ištieskite vidurinį pirštą taip, kad jis būtų nukreiptas į kairę, o visi pirštai būtų statmeni vienas kitam.
Jei turite du vektorius, kuriuos norite padauginti kryžminiu būdu, galite nustatyti išeinančio vektoriaus kryptį rodydami nykščiu pirmojo vektoriaus kryptimi, o rodykle - antrojo vektoriaus kryptimi. Vidurinis pirštas rodys kryžminės sandaugos kryptį.
Atminkite, kad pakeitus vektorių kryžminio dauginimo tvarką, rezultatas bus atvirkštinis. Todėl svarbu įsitikinti, kad eisite tokia tvarka: t h u m b → × p o i n t e r → = m i d l e → {\displaystyle {\vec {thumb}}\times {\vec {pointer}}={\vec {middle}}}. 
Kas yra kryžminė sandauga?
Kryžminė (vektorių kryžminė) sandauga dviejų trimačių vektorių a ir b yra trečias vektorius, kuris yra statmenas abiem pradinių vektorių kryptims. Kryžminės sandaugos kryptį nustato dešiniosios rankos taisyklė, o jos ilgis lygus abiejų vektorių ilgių sandaugai iš sinuso jų kampo:
- Kryptis: statmena abiem vektoriams, nustatoma dešiniosios rankos taisykle.
- Modulis: |a × b| = |a| |b| sin θ, kur θ yra kampas tarp a ir b (0 ≤ θ ≤ π).
Matematinė formulė ir koordinatės
Trimatėje (x, y, z) erdvėje, jei a = (a1, a2, a3) ir b = (b1, b2, b3), tada kryžminė sandauga yra
(a × b) = (a2 b3 − a3 b2, a3 b1 − a1 b3, a1 b2 − a2 b1).
Dažnai tai užrašoma kaip determinantas su vienetinių vektorių eilute:
i j k
a1 a2 a3
b1 b2 b3
Pagrindinės savybės
- Anti-komutatyvumas: a × b = − (b × a). Tai reiškia, kad pakeitus eiliškumą, kryptis apsiverčia.
- Distributyvumas: a × (b + c) = a × b + a × c.
- Nėra asociatyvumo: (a × b) × c ≠ a × (b × c) iš esmės.
- Nulis: Jei vektoriai yra lygiagretūs arba vienas iš jų yra nulio, kryžminė sandauga yra nulio vektorius (sin θ = 0).
Pritaikymas fizikoje ir inžinerijoje
- Momentas (sukimo momentas): τ = r × F — jėgos sukuriamas sukimo momentas aplink tašką.
- Magnetinė jėga: F = q v × B — krūvinio dalelės patiriama jėga magnetiniame lauke.
- Normalės vektoriai: plokštumos arba paviršiaus normalė randama kaip dviejų jos vektorių kryžminė sandauga.
Praktiniai patarimai ir atsargumo priemonės
- Visada nusistatykite aiškią vektorių tvarką: pirmasis vektorius atitinka nykštį, antrasis — rodyklę, o rezultatas bus vidurinis pirštas.
- Būkite atsargūs naudodami kitokias taisykles (pvz., kairiosios rankos taisyklę) — jos duoda priešingą kryptį ir gali sukelti klaidas, jei nebus aišku, kuri sistema naudojama.
- Atkreipkite dėmesį į vienetus ir matmenis: kryžminė sandauga priklauso nuo vektorių ilgių ir kampo tarp jų.
Ši taisyklė — paprastas ir veiksmingas būdas nusakyti kryžminės sandaugos kryptį praktikoje: nuo uždavinių matematikoje iki realių fizikos ir inžinerijos uždavinių.

Dešiniosios rankos taisyklė judėjimui, atliekamam su sraigtiniais sriegiais

Kairės pusės orientacija parodyta kairėje, o dešinės pusės - dešinėje.
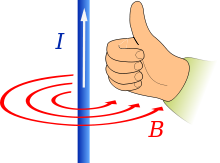
Lauko krypties prognozė (B), kai srovė I teka nykščio kryptimi
Variantai
Yra dar viena taisyklė, vadinama dešiniosios rankos laikymo taisykle (arba kamštinio sraigto taisykle), kuri taikoma magnetiniams laukams ir daiktams, kurie sukasi.
1. Pradėkite ištiesę dešinę ranką ir ištieskite nykštį taip, kad jis būtų stačiu kampu su kitais pirštais.
2. Dabar suspauskite pirštus į kumštį, o nykštį laikykite ištiestą (kaip nykštį į viršų).
3. Palyginkite, kaip jūsų pirštai sukiojasi pagal tai, kaip kas nors juda. Kryptis, kurią rodo jūsų nykštys, yra vektoriaus, kurį naudojame kalbėdami apie tai, kryptis.
Tai galite padaryti ir atvirkščiai, pradėdami nykščiu judėti vektoriaus kryptimi ir stebėdami, kaip sukasi pirštai, kad pamatytumėte sukimosi kryptį. Jei nykštį nukreipsite laidu tekančios srovės kryptimi, aplink jį atsirandantis magnetinis laukas bus jūsų susuktų pirštų kryptimi.
Klausimai ir atsakymai
K: Kas yra dešiniosios rankos taisyklė?
Atsakymas: Dešiniosios rankos taisyklė - tai vektorių matematikos konvencija, kuri padeda prisiminti kryptį, kai vektoriai dauginami kryžminiu būdu.
K: Kaip naudojate dešiniosios rankos taisyklę, norėdami sužinoti kryžminės sandaugos kryptį?
A: Norėdami sužinoti kryžminės sandaugos kryptį, uždarykite dešinę ranką ir ištieskite rodomąjį pirštą. Nykštį iškelkite tiesiai į viršų, tarsi darytumėte pistoleto ženklą. Nukreipkite "pistoletą" tiesiai į priekį, tada ištieskite vidurinį pirštą taip, kad jis būtų nukreiptas į kairę, o visi pirštai būtų statmeni vienas kitam. Nykštį nukreipkite pirmojo vektoriaus kryptimi, o rodomąjį pirštą - antrojo vektoriaus kryptimi. Vidurinis pirštas bus nukreiptas kryžminės sandaugos kryptimi.
Klausimas: Kas atsitiks, jei pasikeis tvarka, kai vektoriai bus kryžminės sandaugos?
A: Kai keičiate tvarką, kai vektoriai dauginami kryžmine sandauga, rezultatas eina priešingomis kryptimis. Todėl svarbu įsitikinti, kad einate tokia tvarka: nykštys x rodyklė = vidurinysis .
K: Ką reiškia ši lygtis? {\displaystyle {\vec {thumb}}\times {\vec {pointer}}={\vec {middle}}} .
A: Ši lygtis reiškia, kad jei du vektoriai bus sukryžiuoti ir padauginti vienas iš kito (nykštys x rodyklė), gausime trečią vektorių (vidurį).
Ieškoti