Fi
Vieną skaičių a ir kitą mažesnį skaičių b dalijant randamas šių dviejų skaičių santykis. Jų santykis yra a/b. Kitas santykis randamas sudėjus abu skaičius a+b ir padalijus iš didesniojo skaičiaus a. Naujasis santykis yra (a+b)/a. Jei šie du santykiai yra lygūs tam pačiam skaičiui, tas skaičius vadinamas aukso santykiu. Graikiška raidė φ {\displaystyle \varphi } 
(phi) paprastai vartojama kaip aukso pjūvio pavadinimas.
Pavyzdžiui, jei b = 1 ir a/b = φ {\displaystyle \varphi } tada a = φ {\displaystyle \varphi }, tada a = φ {\displaystyle \varphi } . Antrasis santykis (a+b)/a tada yra ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi } 
. Kadangi šie du santykiai yra lygūs, tai yra tiesa:
φ = φ + 1 φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}}
Vienas iš būdų užrašyti šį skaičių yra
φ = 1 + 5 2 {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}}
5 {\displaystyle {\sqrt {5}}}
yra panašus į bet kurį skaičių, kurį padauginus iš savęs gaunamas 5 (arba kuris skaičius yra padaugintas): 5 × 5 = 5 {\displaystyle {\sqrt {5}} kartų {\sqrt {5}}=5}}
.
Aukso pjūvis yra iracionalusis skaičius. Jei žmogus pabandys jį užrašyti, jis niekada nesustos ir nesudarys rašto, bet prasidės taip: 1,6180339887... Svarbus dalykas apie šį skaičių yra tai, kad žmogus gali iš jo atimti 1 arba padalyti 1 iš jo. Bet kuriuo atveju skaičius vis tiek tęsis ir niekada nesustos.
Auksinis stačiakampis
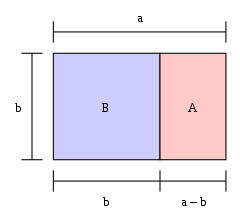
Jei stačiakampio ilgis, padalytas iš pločio, yra lygus aukso pjūviui, stačiakampis yra "auksinis stačiakampis". Jei nuo vieno auksinio stačiakampio galo nupjaunamas kvadratas, kitas jo galas yra naujas auksinis stačiakampis. Paveikslėlyje didelis stačiakampis (mėlynas ir rožinis kartu) yra auksinis stačiakampis, nes a / b = φ {\displaystyle a/b=\varphi } 
. Mėlynoji dalis (B) yra kvadratas. Rausvoji dalis (A) yra dar vienas auksinis stačiakampis, nes b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi } 
. Didžiojo stačiakampio ir rožinio stačiakampio forma yra tokia pati, tačiau rožinis stačiakampis yra mažesnis ir pasuktas.
Didysis stačiakampis BA yra auksinis stačiakampis, t. y. santykis b:a yra 1: φ {\displaystyle \varphi } . Jei iš bet kurio tokio stačiakampio pašalinsime kvadratą B, liks A, t. y. kitas auksinis stačiakampis, kurio proporcijos tokios pat kaip pradinio stačiakampio.
Fibonačio skaičiai
Fibonačio skaičiai yra skaičių sąrašas. Kitą skaičių sąraše galima rasti sudėjus du paskutinius skaičius. Jei žmogus padalys sąrašo skaičių iš prieš tai buvusio skaičiaus, šis santykis vis labiau priartės prie aukso pjūvio.
| Fibonačio skaičius | padalytas iš prieš tai buvusio | santykis |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ {\displaystyle \varphi } | = 1.6180... |
Aukso pjūvis gamtoje
Gamtoje aukso pjūvis dažnai naudojamas lapams ar gėlėms išdėstyti. Juose naudojamas auksinis kampas, kurio kampas yra maždaug 137,5 laipsnio. Tokiu kampu išdėstyti lapai ar gėlės geriausiai išnaudoja saulės šviesą.
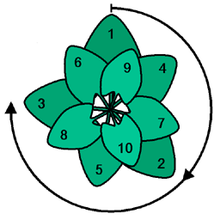
Naudodami auksinį kampą optimaliai išnaudosite saulės šviesą. Tai vaizdas iš viršaus.
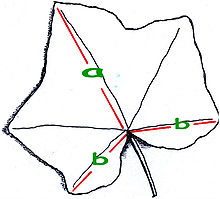
Paprastosios gebenės lapas, rodantis aukso pjūvį
Klausimai ir atsakymai
K: Koks yra dviejų skaičių santykis?
Atsakymas: Dviejų skaičių santykis randamas juos dalijant, taigi santykis būtų a/b.
K: Kaip galima rasti kitą santykį?
A: Kitą santykį galima rasti sudėjus du skaičius ir padalijus šią sumą iš didesniojo skaičiaus a. Šis naujas santykis būtų (a+b)/a.
K: Kaip vadinama, kai šie du santykiai yra lygūs vienas kitam?
A: Kai šie du santykiai yra lygūs vienas kitam, tai vadinama aukso pjūviu. Jis paprastai žymimas graikiška raide צ arba phi.
K: Jei b = 1, o a/b = צ , ką tai reiškia a?
A: Jei b = 1 ir a/b = צ , tai reiškia, kad ir a = צ .
K: Kaip galima užrašyti šį skaičių?
Atsakymas: Vienas iš būdų užrašyti šį skaičių yra צ = 1 + 5 / 2 = 1,618...
K: Ką reiškia, jei iš šio skaičiaus atimsime 1 arba padalinsime iš jo 1?
Atsakymas: Jei iš jo atimsite 1 arba iš jo padalysite 1, gausite atgal tą patį skaičių, kitaip tariant, jie abu bus lygūs aukso santykiui.
K: Ar aukso santykis yra iracionalusis skaičius?
A: Taip, aukso santykis yra iracionalusis skaičius, o tai reiškia, kad jei kas nors pabandys jį užrašyti, niekada nebus pabaigos ir jokio modelio - tik pradedant kažkuo panašiu į "1,6180339887...".
