Lygiagretumo postulatas (penktasis Euklido postulatas) — apibrėžimas
Lygiagretumo postulatas (penktasis Euklido post.) — aiškus apibrėžimas, istorija ir reikšmė geometrijoje: supraskite euklidinės ir neeuklidinės geometrijos skirtumus.
Geometrijoje lygiagretusis postulatas yra viena iš Euklido geometrijos aksiomų. Kartais jis dar vadinamas penktuoju Euklido postulatu, nes yra penktasis Euklido veikalo "Elementai" postulatas.
Originali Euklido formuluotė skamba taip:
Jei tiesės atkarpą nupjaunate dviem tiesėmis, o du vidiniai kampai, kuriuos sudaro šios tiesės, yra mažesni nei 180°, tai abi tiesės galiausiai susikirs, jei jas pratęsite pakankamai ilgai.
Postulato aiškinimas paprastai kalba
Trumpai tariant, postulatas reguliuoja lygiagrečių tiesių elgesį plokštumoje: jis nurodo, kada dvi tiesės susikirs arba liks lygiagrečios. Nors Euklidas pateikė šį teiginį kaip aksiomą (nes, jo manymu, aiškiai matoma), vėlesni matematikai pastebėjo, kad šis postulatas turi kitokio pobūdžio prigimtį nei kitos Euklido aksiomos — jis neišvedamas paprastais logikos ar geometrijos samprotavimais iš kitų postulatų.
Ekvivalentinės formuluotės
Lygiagretumo postulatas turi kelias lygiavertes ir dažniau vartojamas formuluotes. Svarbiausios:
- Playfair axiom: Per tašką, kuris nėra duotos tiesės dalis, eina tik viena tiesė, kuri yra lygiagreti duotajai tiesei.
- Trikampio kampų suma: Kiekvieno trikampio trijų kampų suma yra lygi 180° (dviems stačioms kampams).
- Egzistuoja stačiakampis: Jei egzistuoja vienas stačiakampis, tuomet galioja lygiagretumo postulatas visai plokštumai (šis teiginys pateikiamas kaip ekvivalentas kai kuriose axiom sistemose).
Istorija ir nepriklausomumas
Keletą šimtmečių matematikai mėgino įrodyti penktąjį postulatą iš likusių Euklido aksiomų, manydami, jog jis galėtų būti nereikalingas. Bandymų ratas vedė prie didelių atradimų XIX a., kai matematikai kaip J. Bolyai, N. I. Lobachevsky ir C. F. Gauss suprato, kad penktasis postulatatas yra nepriklausomas nuo kitų: galima sukurti nuoseklias geometrijas, kuriose penktasis postulatatas neatitinka tikrovės, bet sistema lieka kontradikcijų neturinti.
Pasekmės ir reikšmė
Penktasis postulatatas lemia daugelį klasikinių euklidinės geometrijos savybių. Kai jis taikomas, galioja:
- Trikampio kampų suma = 180°;
- paralelinių tiesių savybės pagal Playfair teoremą (vienintelė paralelė per tašką išorinėje tiesėje);
- tam tikrų panašumo ir panašių trikampių egzistavimas bei kitų planimetrinių teoremų galiojimas.
Neeuklidinės geometrijos alternatyvos
Jei penktasis postulatatas pakeičiamas arba atmetamas, gaunamos dvi pagrindinės neeuklidinės geometrijos rūšys:
- Hiperbolinė geometrija (Lobachevsky, Bolyai): per tašką, esančią už duotos tiesės, praeina daugiau nei viena lygiagreti tiesė; trikampio kampų suma yra mažesnė nei 180°.
- Eliptinė (sferinė) geometrija (Riemann): jokios dvi „tiesės“ (didžiosios apskritimų) nesikerta; trikampio kampų suma yra didesnė nei 180°.
Praktinis paveldas
Lygiagretumo postulatas ne tik fundamentaliai veikia plokštuminę geometriją, bet ir turi įtakos šiuolaikinei matematikai bei fizikoms: skirtumai tarp plokštuminės, hiperbolinės ir eliptinės geometrijos susiję su erdvės kreivumu, kurį nagrinėja diferencialinė geometrija ir bendroji reliatyvumo teorija. Išryškėjus penktojo posto nepriklausomybei, matematikai suprato, kad įvairios geometrijos yra vienodai nuoseklios ir tinkamos skirtingiems fizikos bei matematikos modeliams.
Geometrijos sritis, kurioje laikomasi visų Euklido aksiomų, vadinama euklidine geometrija. Geometrija, kurioje laikomasi ne visų Euklido aksiomų, vadinama neeuklidine geometrija.
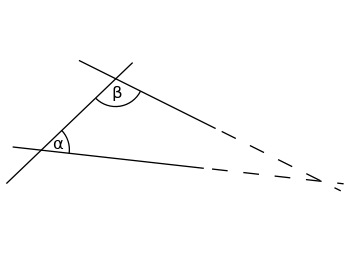
Jei vidinių kampų α (alfa) ir β (beta) suma yra mažesnė nei 180°, abi tiesės susikerta, jei abi yra pratęstos iki begalybės.
Istorija
Kai kurie matematikai manė, kad penktasis Euklido postulatas yra daug ilgesnis ir sudėtingesnis už kitus keturis postulatus. Daugelis jų manė, kad jį galima įrodyti remiantis kitomis paprastesnėmis aksiomomis. Kai kurie matematikai paskelbė, kad įrodė šį teiginį iš paprastesnių postulatų, tačiau paaiškėjo, kad jie visi klydo.
Playfairo aksioma
Kitas naujesnis teiginys, žinomas kaip Playfair'o aksioma, yra panašus į Euklido penktąjį postulatą. Jis teigia, kad:
Turint tiesę ir tašką, esantį ne ant šios tiesės, per šį tašką galima nubrėžti tik vieną tiesę, kuri nesutaps su kita tiese.
Iš tikrųjų matematikai nustatė, kad ši aksioma ne tik panaši į penktąjį Euklido postulatą, bet ir turi lygiai tokią pačią reikšmę. Matematiškai šie du teiginiai vadinami "lygiaverčiais" teiginiais. Šiandien Playfairo aksioma matematikų naudojama dažniau nei originalus lygiagretusis Euklido postulatas.
Neeuklidinė geometrija
Ilgainiui kai kurie matematikai pabandė sukurti naujas geometrijas nenaudodami aksiomos. Viena iš neeuklidinės geometrijos rūšių vadinama elipsine geometrija. Elipsinėje geometrijoje lygiagretainio postulatas pakeistas aksioma, kuri teigia, kad:
Turint tiesę ir tašką, esantį ne ant šios tiesės, negalima nubrėžti tiesės per šį tašką, kuri galiausiai nekirstų kitos tiesės.
Matematikai pastebėjo, kad pakeitę penktąjį Euklido postulatą šia aksioma, jie vis tiek galėjo įrodyti daugelį kitų Euklido teiginių. Vienas iš būdų įsivaizduoti elipsinę geometriją - galvoti apie gaublio paviršių. Žemės rutulyje ilgumos linijos atrodo lygiagrečios ties ekvatoriumi, tačiau visos jos susikerta ties ašigaliais. XIX a. pabaigoje buvo įrodyta, kad elipsinė geometrija yra nuosekli. Tai įrodė, kad penktasis Euklido postulatas nėra nepriklausomas nuo kitų postulatų. Po to matematikai dažniausiai nustojo bandyti įrodyti penktąjį postulatą iš kitų keturių postulatų. Vietoj to daugelis matematikų ėmė tyrinėti kitas geometrijas, kurios nesivadovauja penktuoju Euklido postulatu.
Kita aksioma, kuria matematikai kartais pakeičia penktąją Euklido aksiomą, sako, kad:
Turėdami tiesę ir tašką, esantį ne ant šios tiesės, galite nubrėžti bent dvi tieses per šį tašką, kurios galiausiai nekirs kitos tiesės.
Tai vadinama hiperboline geometrija.
Kita geometrija tiesiog pašalina penktąjį Euklido postulatą ir jo niekuo nepakeičia. Tai vadinama neutralia geometrija arba absoliučia geometrija.
Ieškoti