Tikimybinio tankio funkcija
Tikimybinio tankio funkcija - tai funkcija, kurią galima apibrėžti bet kokiam tolydžiam tikimybiniam pasiskirstymui. Tikimybės tankio funkcijos integralas intervale [ a , b ] {\displaystyle [a,b]} ![{\displaystyle [a,b]}](https://www.alegsaonline.com/image/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)
duoda tikimybę, kad tam tikras atsitiktinis kintamasis, turintis duotą tankį, yra pateiktame intervale.
Tikimybinio tankio funkcija reikalinga norint dirbti su tolydžiaisiais skirstiniais. Išmetus kauliuką bus gauti skaičiai nuo 1 iki 6, o tikimybė 1 6 {\displaystyle {\tfrac {1}{6}}} 
Tačiau tai nėra tolydi funkcija, nes galimi tik skaičiai nuo 1 iki 6. Priešingai, dviejų žmonių ūgis ar svoris nebus vienodas. Naudojant tikimybės tankio funkciją, galima nustatyti tikimybę, kad žmonių ūgis bus nuo 180 cm iki 181 cm arba nuo 80 kg iki 81 kg, nors tarp šių dviejų ribų yra be galo daug reikšmių.
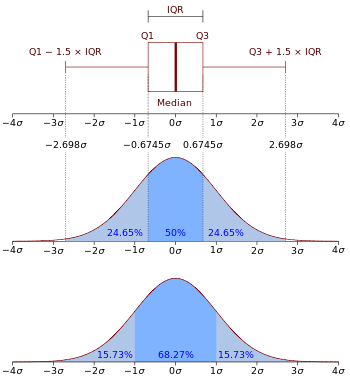
Normaliojo pasiskirstymo N(0, σ2) skritulinė diagrama ir tikimybės tankio funkcija.
Klausimai ir atsakymai
K: Kas yra tikimybės tankio funkcija?
Atsakymas: Tikimybės tankio funkcija - tai funkcija, apibūdinanti bet kokį ištisinį tikimybės pasiskirstymą.
K: Kaip užrašoma atsitiktinio kintamojo X tikimybės tankio funkcija?
A: X tikimybės tankio funkcija kartais užrašoma kaip f_X(x).
K: Ką reiškia tikimybės tankio funkcijos integralas?
Atsakymas: Tikimybės tankio funkcijos integralas parodo tikimybę, kad duotasis atsitiktinis kintamasis, turintis duotąjį tankį, yra pateiktame intervale.
Klausimas: Ar tikimybės tankio funkcija visada yra neneigiama visoje savo srityje?
A: Taip, pagal apibrėžimą tikimybės tankio funkcija yra neneigiama visoje savo srityje.
Klausimas: Ar integruojant per intervalą gaunama suma lygi 1?
A: Taip, integravimas per intervalą yra lygus 1.
K: Kokio tipo pasiskirstymą apibūdina tikimybės tankio funkcija?
A: Tikimybinio tankio funkcija apibūdina bet kokį tolydųjį tikimybinį pasiskirstymą.
