Furjė eilutė
Džozefas Furjė teigė, kad sinusoidėmis galima aproksimuoti kitą funkciją. Tai yra eilutė matematine prasme. Šią teoriją galima apibendrinti Furjė transformacijai. Šių funkcijų matematinė analizė vadinama Furjė analize.
XVIII a. tokie matematikai kaip Euleris, Lagrange'as ir Bernoulli jau naudojo sinusoides kitoms funkcijoms aproksimuoti ir modeliuoti. Kai 1822 m. Fourier paskelbė darbą apie šilumą, jis teigė, kad tokios aproksimacijos egzistuoja bet kuriai tokiai funkcijai (kuri yra tolydi intervale). Iš pradžių žmonės juo netikėjo, ir prireikė beveik dešimties metų, kol pasirodė (dalies problemos) įrodymas.
Šiandien Furjė eilutės plačiai naudojamos skaitmeninių signalų apdorojime.
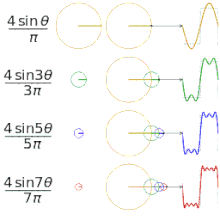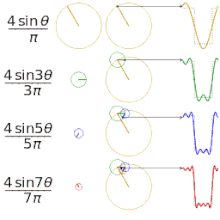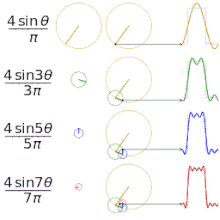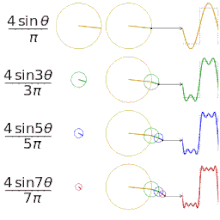
Įvairių "kvadratinių" funkcijų aproksimavimas naudojant Furjė eilutes
Klausimai ir atsakymai
Klausimas: Kas buvo Džozefas Furjė?
A: Žozefas Furjė buvo prancūzų matematikas, pasiūlęs, kad sinusoidės gali būti naudojamos kitai funkcijai aproksimuoti.
K: Kas yra Furjė eilutė?
A: Furjė eilutė - tai eilutė, kurioje sinusoidės naudojamos kitai funkcijai aproksimuoti.
K: Kas yra Furjė transformacija?
A: Furjė transformacija yra apibendrinta teorija, kurioje sinusoidės naudojamos kitai funkcijai aproksimuoti.
K: Kas yra Furjė analizė?
A: Furjė analizė - tai matematinė funkcijų, kurios naudoja sinusoidę kitai funkcijai aproksimuoti, analizė.
K: Kas XVIII a. naudojo sinusoides kitoms funkcijoms aproksimuoti ir modeliuoti?
A: XVIII a. tokie matematikai, kaip Euleris, Lagranžas ir Bernoulli, naudojo sinusoides kitoms funkcijoms aproksimuoti ir modeliuoti.
K: Ką 1822 m. Fourier pasiūlė savo darbe apie šilumą?
A: 1822 m. savo darbe apie šilumą Furjė pasiūlė, kad tokios aproksimacijos naudojant sinusoidę egzistuoja bet kuriai ištisinei funkcijai tam tikrame intervale.
K: Kaip Furjė eilutės naudojamos skaitmeninių signalų apdorojime?
A: Furjė eilės dažnai naudojamos skaitmeniniame signalų apdorojime signalams aproksimuoti ir analizuoti.
