Furjė transformacija
Furjė transformacija - tai matematinė funkcija, kurią galima naudoti signalą ar bangą sudarantiems baziniams dažniams nustatyti. Pavyzdžiui, jei grojamas akordas, jo garso bangą galima įtraukti į Furjė transformaciją ir rasti natas, iš kurių sudarytas akordas. Furjė transformacijos išvestis kartais vadinama dažnių spektru arba pasiskirstymu, nes ji rodo įėjimo dažnių spektrą. Ši funkcija plačiai naudojama kriptografijoje, okeanografijoje, mašininiame mokyme, radiologijoje, kvantinėje fizikoje, taip pat garso dizaine ir vizualizacijoje.
Funkcijos f ( x ) {\displaystyle f(x)}
Furjė transformacija yra tokia
F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx} 
α {\displaystyle \alpha } 
yra dažnis
F ( α ) {\displaystyle F(\alpha )}
yra Furjė transformacijos funkcija ir grąžina vertę, rodančią, koks dažnis α {\displaystyle \alpha } vyrauja pradiniame signale.
e - 2 π i α x {\displaystyle e^{-2\pi i\alpha x}} 
Atvaizduoja įvesties funkcijos f ( x ) {\displaystyle f(x)} apvyniojimą aplink pradžią kompleksinėje plokštumoje tam tikru dažniu α {\displaystyle \alpha }
Atvirkštinė Furjė transformacija yra tokia
f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha }d\alpha } 
Furjė transformacija parodo, kokie dažniai yra signale. Pavyzdžiui, paimkime garso bangą, kurioje yra trys skirtingos muzikos natos: Atlikus šios garso bangos Furjė transformacijos grafiką (x ašyje pavaizduotas dažnis, o y ašyje - intensyvumas), kiekviename dažnyje matysime viršūnę, atitinkančią vieną iš muzikos natų.
Sudedant skirtingų amplitudžių ir dažnių kosinusus ir sinusus galima sukurti daugybę signalų. Furjė transformacija vaizduoja šių kosinusų ir sinusų amplitudes ir fazes pagal jų atitinkamus dažnius.
Furjė transformacijos yra svarbios, nes daugelis signalų įgauna daugiau prasmės, kai jų dažniai yra atskirti. Pirmiau pateiktame garso pavyzdyje, žiūrint į signalą laiko atžvilgiu, nėra akivaizdu, kad signale yra natos A, B ir C. Daugelis sistemų skirtingiems dažniams daro skirtingus dalykus, todėl tokio tipo sistemas galima apibūdinti pagal tai, ką jos daro kiekvienam dažniui. Pavyzdys - filtras, kuris blokuoja aukštus dažnius.
Norint apskaičiuoti Furjė transformaciją, reikia išmanyti integravimą ir įsivaizduojamuosius skaičius. Paprastai Furjė transformacijoms apskaičiuoti naudojami kompiuteriai, išskyrus paprasčiausius signalus. Greitoji Furjė transformacija - tai metodas, kurį kompiuteriai naudoja Furjė transformacijai greitai apskaičiuoti.
· 
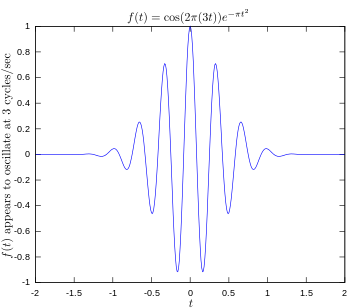
Originali funkcija, rodanti 3 hercų dažniu svyruojantį signalą.
· 
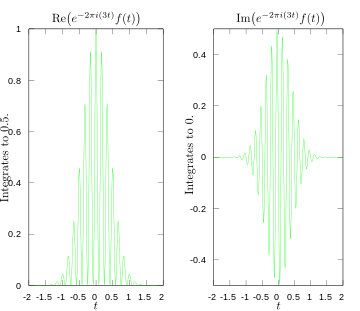
Integranto realioji ir įsivaizduojamoji dalys Furjė transformacijai esant 3 hercų dažniui
· 
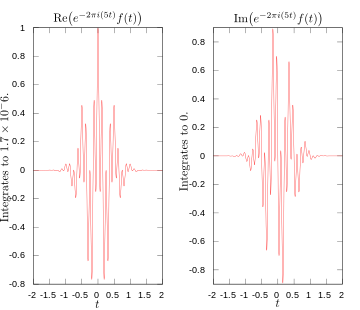
Integranto realioji ir įsivaizduojamoji dalys Furjė transformacijai esant 5 hercų dažniui
· 
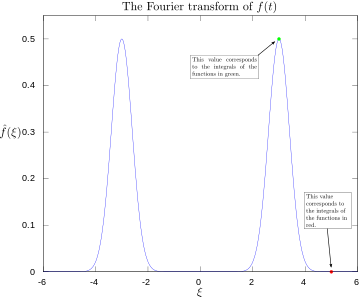
Furjė transformacija su pažymėtais 3 ir 5 hercais.
Klausimai ir atsakymai
K: Kas yra Furjė transformacija?
A: Furjė transformacija yra matematinė funkcija, kuria galima rasti bazinius dažnius, iš kurių sudaryta banga. Ji paima kompleksinę bangą ir suranda ją sudarančius dažnius, iš kurių galima nustatyti akordą sudarančias natas.
Klausimas: Kokie yra kai kurie Furjė transformacijos panaudojimo būdai?
A: Furjė transformacija plačiai naudojama kriptografijoje, okeanografijoje, mašinų mokyme, radiologijoje, kvantinėje fizikoje, taip pat garso dizaine ir vizualizacijoje.
K: Kaip apskaičiuojama Furjė transformacija?
A: Funkcijos f(x) Furjė transformacija gaunama pagal formulę F(ב) = ∫-∞+∞f(x)e-2נiבxdx, kur ב yra dažnis. Grąžinama vertė, rodanti, kiek dažnis ב paplitęs pradiniame signale. Atvirkštinė Furjė transformacija yra tokia: f(x) = ∫-∞+∞F(ב)e+2נixבdב.
K: Kaip atrodo Furjė transformacijos išvestis?
A: Furjė transformacijos išvestį galima vadinti dažnių spektru arba pasiskirstymu, nes ji rodo galimų įėjimo dažnių pasiskirstymą.
K: Kaip kompiuteriai apskaičiuoja greitąsias Furjė transformacijas?
A: Kompiuteriai naudoja algoritmą, vadinamą greitąja Furjė transformacija (angl. Fast Fourier Transform, FFT), kad greitai apskaičiuotų bet kokias, išskyrus paprasčiausias signalų transformacijas.
K: Ko neparodo signalų nagrinėjimas laiko atžvilgiu?
A: Žiūrint į signalus laiko atžvilgiu, neaišku, kokios natos juose skamba; daugelį signalų geriau suprasti, kai jų dažniai atskiriami ir analizuojami atskirai.
