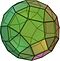
Archimedo kūnai — geometrijos simetriški kietieji daugiakampiai

Archimedo kūnai: simetriški geometrijos kietieji daugiakampiai, jų tipai (13/15), konstrukcijos ir istorija nuo Archimedo iki Keplerio — įdomus vadovas apie formų simetriją.

Autorius: Leandro Alegsa

19-01-2026 17:26

Geometrijoje Archimedo kūnas yra konveksinis, simetriškas kietasis daugiakampis, sudarytas iš daugiakampių, kurių kiekvienas veidas yra taisyklingas daugiakampis. Tai ypatinga daugiakampio rūšis: jos viršūnių aplinka (kampų išsidėstymas aplink kiekvieną viršūnę) yra vienoda visose viršūnėse, o pačios figūros briaunos turi vienodą ilgį. Archimedo kūnai vengia kai kurių kitų tipinių kategorijų — ši forma nėra nei platoniškasis kietasis kūnas, nei prizmė, nei antiprizma.

Svarbiausios savybės

Kiekvienas veidas yra taisyklingas daugiakampis. Veidų tipų paprastai yra du ar daugiau, tačiau kiekvienas veidas yra reguliari figūra (pvz., trikampis, kvadratas, penkiakampis).
Visi figūros kampai atrodo vienodi. Kitaip tariant, visose viršūnėse sutampa veidų išsidėstymas ir kampų kombinacija (viršūninis konfigūracija yra vienoda) — ši savybė vadinama viršūnių tranzityvumu (vertex-transitivity).
Vienodos briaunos. Visos briaunos turi tą patį ilgį, todėl figūra yra „uniformi“.

Priklausomai nuo skaičiavimo būdo, tokių figūrų yra trylika arba penkiolika: yra 13 Archimedo kūnų, o jei atskirai skaičiuojamos dvi chiralinės (veidrodinės) versijos, susidaro 15. Dvi iš šių figūrų turi dvi nesutapatinamas pasukimu versijas (chirališkos poros), todėl kartais minima 15 formų. Sutapatinti (arba laisvai pasukti) kai kurių jų negalima — jos būna enantiomorfiškos.

Trumpa istorija

Archimedo kūnai pavadinti senovės graikų matematiko Archimedo, vardu. Pats Archimedas, greičiausiai III a. pr. m. e., aprašė šias formas, bet jo raštai vėliau dingo; jų fragmentus ir apibendrinimus pateikė IV a. Pappas iš Aleksandrijos. Renesanso laikais menininkai ir matematikai vėl susidomėjo „grominėmis“ (grynosiomis) formomis ir iš naujo atrado bei piešė šias figūras. Johannesas Kepleris ir kiti XVII a. mokslininkai pratęsė šį darbą; vėlesni matematikai įrodė, kad pateiktas Archimedo kūnų sąrašas yra išsamus.

Kas įeina į Archimedo kūnus?

Įprastinis 13 Archimedo kūnų sąrašas (su dažniausiai vartojamais pavadinimais anglų kalba) apima:

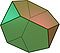
Truncated tetrahedron (apkarpytasis keturbriaunis)
Cuboctahedron (kuboctaedras)
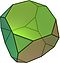
Truncated cube (apkarpytasis kubas)
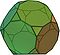
Truncated octahedron (apkarpytasis aštuoniabriaunis)
Rhombicuboctahedron (mažasis rombinis kuboctahedron arba rhombicuboctahedron)
Truncated cuboctahedron (didelis rombinis kuboctahedron, dar vadinamas truncated cuboctahedron)
Snub cube (snub cube — yra chiralinė pora)
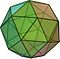
Icosidodecahedron (icosidodecahedron)
Truncated dodecahedron (apkarpytasis dodekaedras)
Truncated icosahedron (apkarpytasis ikosaedras — garsus kaip fullerenas C60, „futbolo“ forma)
Rhombicosidodecahedron (rhombicosidodecahedron)
Truncated icosidodecahedron (truncated icosidodecahedron)
Snub dodecahedron (snub dodecahedron — taip pat chiralinė pora)

Pastaba: daugelio pavadinimų tradiciniai lietuviški atitikmenys nenaudojami visuose šaltiniuose, todėl dažnai vartojami angliški terminai.

Dualai ir pritaikymas

Kiekvienas Archimedo kūnas turi savo dualią figūrą — jos dualai priklauso vadinamiesiems Katalano kūnams (Catalan solids). Archimedo kūnai ir jų dualai dažnai naudojami architektūroje, meno kūriniuose, modeliavime ir chemijoje (pavyzdžiui, truncated icosahedron formą atitinka C60 fullerenas).

Apibendrinant: Archimedo kūnai — tai taisyklingų daugiakampių sudaromos, viršūnėse vienodai išsidėsčiusios, uniformios ir estetiškai simetriškos konveksinės figūros; jų tyrimas jungia geometriją, meną ir taikomąsias sritis.

Archimedo kietajam kūnui sudaryti reikia bent dviejų skirtingų daugiakampių.

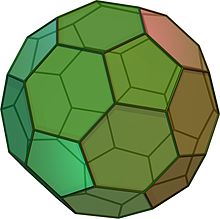
Nukirstas ikosaedras atrodo kaip futbolo kamuolys. Jis sudarytas iš 12 lygiakraščių penkiakampių ir 20 taisyklingų šešiakampių. Jis turi 60 viršūnių ir 90 briaunų. Tai Archimedo kūnas

Savybės

Archimediniai kūnai yra sudaryti iš taisyklingų daugiakampių, todėl visos briaunos yra vienodo ilgio.
Visi Archimedo kietieji kūnai gali būti sukurti iš platoniškųjų kietųjų kūnų, "nupjaunant" platoniškojo kūno kraštus.
Daugiakampiai, kurių kampas ("viršūnė") sutampa, būdingi ir archimediškam, ir platoniškam kietajam kūnui.

Ryšys su Platono kūnais

Platono kietieji kūnai gali būti paversti Archimedo kietaisiais kūnais laikantis tam tikrų jų konstravimo taisyklių.

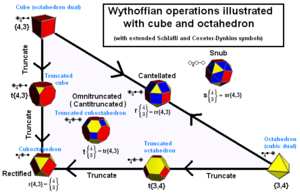
Archimedų kietąsias kūnas galima konstruoti kaip generatoriaus pozicijas kaleidoskope

Archimedo kietųjų kūnų sąrašas

Toliau pateikiamas visų Archimedo kietųjų kūnų sąrašas

Vaizdas	Pavadinimas	Veidai	Tipas	Kraštai	Viršūnės
	Nukirstas tetraedras	8	4 trikampiai 4 šešiakampiai	18	12
	Kuboktaedras	14	8 trikampiai 6 kvadratai	24	12
	Sutrumpintas kubas	14	8 trikampiai 6 aštuonkampiai	36	24
	Nukirstas aštuoniakampis	14	6 kvadratai 8 šešiakampiai	36	24
	Rombokuboktaedras	26	8 trikampiai 18 kvadratų	48	24
	Nukirstas kuboktaedras	26	12 kvadratų 8 šešiakampiai 6 aštuonkampiai	72	48
	"Snub cube" (2 veidrodinės versijos)	38	32 trikampiai 6 kvadratai	60	24
	Ikosidodekaedras	32	20 trikampių 12 penkiakampių	60	30
	Nukirstas dodekaedras	32	20 trikampių 12 dekagonų	90	60
	Nukirstas ikosaedras	32	12 penkiakampių 20 šešiakampių	90	60
	Romboidodekaedras	62	20 trikampių30 kvadratų12 penkiakampių	120	60
	Nukirstas ikosidodekaedras	62	30 kvadratų 20 šešiakampių 12 dekagonų	180	120
	Snubinis dodekaedras (2 veidrodinės versijos)	92	80 trikampių 12 penkiakampių	150	60

Klausimai ir atsakymai

Klausimas: Kas yra Archimedo kietasis kūnas?

A: Archimedo kietasis kūnas yra iš daugiakampių sudaryta išgaubta figūra, kurios kiekvienas paviršius yra taisyklingas daugiakampis, visi kampai atrodo vienodai ir kuri nėra platoniškasis kietasis kūnas, prizmė ar antiprizma.

K: Kiek yra archimedinių kietųjų kūnų?

A: Priklausomai nuo to, kaip jie skaičiuojami, yra trylika arba penkiolika Archimedo kūnų.

K: Kas atrado Archimedo kūnus?

A: Archimedo kietieji kūnai pavadinti senovės graikų matematiko Archimedo, kuris juos atrado tikriausiai III a. pr. m. e., vardu.

K: Ką Pappas iš Aleksandrijos padarė su Archimedo raštais?

A: IV a. Pappas iš Aleksandrijos apibendrino Archimedo raštus apie Archimedo kietuosius kūnus.

K: Kodėl menininkai ir matematikai Renesanso laikotarpiu iš naujo atrado Archimedo kūnus?

A: Renesanso laikotarpiu menininkai ir matematikai vertino grynąsias formas, o Archimedo kietieji kūnai buvo laikomi grynosiomis formomis.

K: Kada Johanesas Kepleris baigė visų Archimedo kūnų paieškas?

A: Johanesas Kepleris tikriausiai baigė visų Archimedo kietųjų kūnų paieškas apie 1620 m.

K: Ko reikia, norint sudaryti Archimedo kietąjį kūną?

A: Archimedo kietajam kūnui sukonstruoti reikia bent dviejų skirtingų daugiakampių.

Ieškoti