Šviesos laikrodis: specialiojo reliatyvumo pavyzdys ir laiko dilatacija

Šviesos laikrodis: aiškus specialiojo reliatyvumo pavyzdys — laiko dilatacijos paaiškinimas su pavyzdžiais, algebra ir Pitagoro teorema.

Šviesos laikrodis — tai paprastas ir aiškus specialiojo reliatyvumo principų pavyzdys. Jis susideda iš stačio stulpo, viršuje pritvirtinto veidrodžio ir apačioje esančio šviesos šaltinio bei detektoriaus. Vienas „tiksėjimas“ atliekamas taip: šviesos blyksnis pakyla nuo apačios iki veidrodžio, atsispindi ir sugrįžta į apačią, kur jį užfiksuoja detektorius. Kiekvienas blyksnis užfiksuojamas skaitikliu — taip „laikrodis“ skaičiuoja akimirkas. Iš šio paprasto įrenginio lengva parodyti, kad stebėtojai, kuriems tas laikrodis juda, matys jo „tiksėjimus“ užsitęsančius — tai ir yra laiko dilatacija, viena iš specialiosios reliatyvumo savybių (specialiojo reliatyvumo). Šį reiškinį taip pat žymima terminu laikodilatacija.

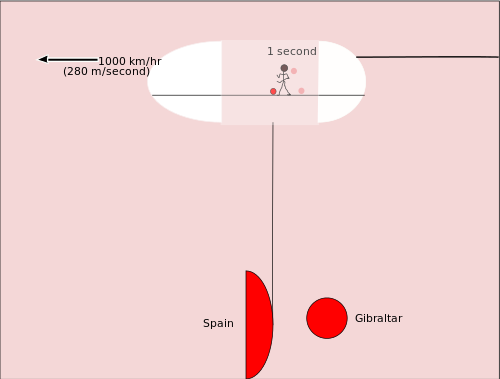
Norint geriau suprasti, kas vyksta, palyginkime su paprastesniu pavyzdžiu: įsivaizduokite krepšininką, driblinantį lėktuvo bagažinėje, kuris juda kartu su lėktuvu. Viduje esantys stebėtojai mato kamuolio trajektoriją aukštyn–žemyn, o išorės stebėtojai mato, kad kartu su kamuoliu persikelia ir vieta Žemės atžvilgiu — todėl per tą patį laiką kamuolys yra judėjęs į priekį (pvz., 280 m). Tai pavyzdys, kaip vienas įvykis skirtingiems stebėtojams gali būti apibūdinamas skirtingais erdvės ir laiko komponentais.

Kaip veikia šviesos laikrodis

Šviesos laikrodis paprastai parenkamas taip, kad atstumas nuo jo apačios iki veidrodžio yra a. Jei laikrodis stovi vietoje (t. y. yra ramybės atžvilgiu), šviesa nueina antrą kelią į viršų ir žemyn, bendra nueito kelio ilgis yra d = 2a. Taigi, jei šviesos greitis yra c, laikas tarp dviejų požiūrių (vieno tiksėjimo) ramybės sistemoje yra

t = 2a / c.

Pavyzdžiui, jei laikrodis yra 0,5 km aukščio (a = 0,5 km), šviesa nueina 1 km kiekvienam tiksėjimui, taigi

t = 1 km / 300 000 km/s = 1/300 000 s ≈ 3,333·10⁻⁶ s (≈ 3,33 µs).

Tačiau jei toks pats laikrodis yra pritvirtintas kosminiam laivui, judančiam greičiau nei stovi stebėtojas (pvz., virš Žemės esančiam stebėtojui laivas juda horizontalia kryptimi dideliu greičiu), stebėtojo matomas šviesos kelias nebe bus vertikalus. Kai blyksnis keliauja į veidrodį, laivo ašis tuo metu pasistumi taip, kad šviesa turi eiti įstrižai. Panaudoję Pitagoro teoremą ir konstanto šviesos greitį, galime apskaičiuoti, kaip pasikeičia laiko intervalas, matomas išorės stebėtojo.

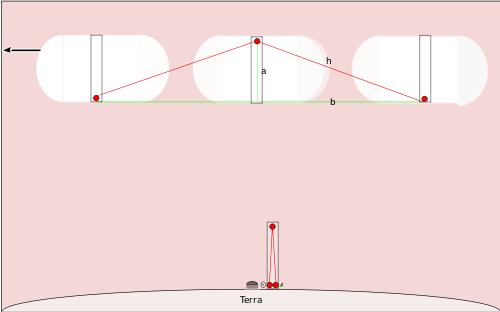
Matematika — laiko dilatacijos išvedimas

Tarkime, kad laivas juda greičiu r horizontalia kryptimi, o stebėtojas Žemėje mato, kad laiko tarpas vienam laivo laikrodžio tiksėjimui yra t'. Kai blyksnis pakyla iki veidrodžio, laivas per tą pusę periodo nuskrenda atstumą (1/2) r t'. Todėl vienos pusės (į viršų) šviesos kelio ilgio hipotenuzė yra

h = √(a² + (r t'/2)²).

Bendra šviesos nueita atstumo iki veidrodžio ir atgal yra d = 2h, o šviesos greitis yra pastovus, taigi

c t' = 2 √(a² + (r t'/2)²).

Išsprendžiant šią lygtį žingsnis po žingsnio (parodoma sutrumpintai):

1. Padauginame abi puses iš 1/2 ir pakeliame kvadratu: (c t'/2)² = a² + (r t'/2)².
2. Perrašome: (c² − r²) t'² / 4 = a².
3. Išsprendžiame dėl t'²: t'² = 4 a² / (c² − r²).
4. Gauname: t' = 2 a / √(c² − r²) = (2 a / c) · 1 / √(1 − r²/c²).

Tačiau prisiminkime, kad laikrodžio ramybės sistemoje t = 2 a / c. Todėl galime užrašyti žinomą reliatyvumo formulę:

t' = t / √(1 − r² / c²),

kurioje faktoriumi γ = 1/√(1 − r²/c²) žymima laiko dilatacija (Lorenco faktorius). Ši formulė rodo, kad stebėtojas, kuriam laikrodis juda greičiu r, matys tiksėjimus rečiau (t. y. trukmė tarp tiksėjimų bus ilgesnė) nei stebėtojas, kuriam laikrodis ramybės būsenoje.

Pavyzdžiai ir fizinis paaiškinimas

• Jei t (laikrodžio savas periodas) būtų 1 s ir laivas judėtų greičiu r = 0,5 c, tuomet γ = 1/√(1 − 0,25) ≈ 1,1547, taigi t' ≈ 1,1547 s. Tai reiškia, kad laive esantis laikrodis per sekundę rodytų vieną tiksėjimą savo sistemoje, o žiūrovas išorėje matytų tą tiksėjimą užsitęsusį iki ~1,1547 s.
• Jei jūsų šviesos laikrodis yra 0,5 km ilgio, jo savas periodas yra ≈3,33 µs. Jei toks laikrodis judėtų r = 0,5 c, išorės stebėtojas matytų periodą padidėjusį iki ≈3,85 µs (padidėjimas tas pats γ ≈1,1547 kartų).

Fizinis paaiškinimas: šviesos greitis yra visiems stebėtojams vienodas. Jei laikrodis juda, vienam stebėtojui šviesa turi nueiti ilgesnį (įstrižą) kelią nei kitam — esant didesniam keliui ir tokiai pačiai šviesos sankirtai, reikia ilgesnio laiko. Todėl judančio laikrodžio judėjimo atžvilgiu matomas laikas „išsitempia“.

Eksperimentinis patvirtinimas ir praktinė reikšmė

Laiko dilatacija nėra vien teorinė, ji buvo patikrinta daugeliu būdų: kosminių spindulių (miuonų, kurie gyvena trumpiau savo ramybės sistemoje, tačiau fiksuojami dažniau Žemės paviršiuje dėl dilatacijos), vykdant tikslų laikrodžių palyginimą greitintuvuose bei GPS palydovų sistemoje (kur reikia taisyti laiką atsižvelgiant į reliatyvistinius efektus, kad vietos nustatymas būtų tikslus).

Jei norite pasimokyti eksperimentuoti skaičiuoklėmis ir pamatyti, kaip keičiasi laiko dilatacija esant įvairiems greičiams, galite naudoti interaktyvią priemonę: http://www.1728.org/reltivty.htm

Klausimai ir atsakymai

K: Kas yra šviesos varpas?

K: Kas yra laiko dilatacija?

K: Kaip apskaičiuoti, kiek sulėtėja laikas erdvėlaivyje?

K: Kaip veikia šviesos laikrodis?

K: Kokios lygties reikia šiam skaičiavimui?

K. Kaip Pitagoro teorema susijusi su šiuo skaičiavimu?

Paieška pagal raidę