Tikimybių erdvė
Tikimybių erdvė - tai matematinis modelis, naudojamas moksliniams eksperimentams aprašyti Tikimybių erdvę sudaro trys dalys:
- Imties erdvė, kurioje išvardyti visi galimi rezultatai
- Įvykių rinkinys. Su kiekvienu įvykiu siejama nulis ar daugiau rezultatų
- Funkcija, kuri kiekvienam įvykiui priskiria tikimybes
Rezultatas yra vieno modelio vykdymo rezultatas. Kadangi atskiri rezultatai gali būti mažai praktiškai naudingi, rezultatų grupėms apibūdinti naudojami sudėtingesni įvykiai. Visų tokių įvykių rinkinys yra σ-algebra F {\displaystyle \scriptstyle {\mathcal {F}}}. 
. Galiausiai reikia nurodyti kiekvieno įvykio atsitikimo tikimybę. Tai atliekama naudojant tikimybės matų funkciją P.
Nustačius tikimybių erdvę, daroma prielaida, kad "gamta" daro savo žingsnį ir iš imties erdvės Ω pasirenka vieną rezultatą ω. Sakoma, kad visi F {\displaystyle \scriptstyle {\mathcal {F}}} įvykiai, kuriuose yra pasirinktas rezultatas ω (prisiminkime, kad kiekvienas įvykis yra Ω poaibis), "įvyko". Gamtos vykdoma atranka atliekama taip, kad jei eksperimentas būtų kartojamas be galo daug kartų, santykiniai kiekvieno įvykio pasireiškimo dažniai sutaptų su funkcijos P nustatytomis tikimybėmis.
Žymus sovietų matematikas Andrejus Kolmogorovas XX a. trečiajame dešimtmetyje kartu su kitomis tikimybių aksiomomis įvedė tikimybinės erdvės sąvoką.
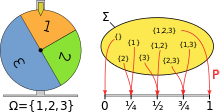
Laimės rato modeliavimas naudojant tikimybių erdvę
Klausimai ir atsakymai
K: Kas yra tikimybių erdvė?
Atsakymas: Tikimybių erdvė - tai matematinis modelis, naudojamas moksliniams eksperimentams aprašyti. Ją sudaro trys dalys: imties erdvė, kurioje išvardijamos visos galimos baigtys, įvykių rinkinys, su kuriuo siejama nulis ar daugiau baigčių, ir funkcija, kuri kiekvienam įvykiui priskiria tikimybes.
Klausimas: Iš ko susideda imties erdvė?
A: Imties erdvę sudaro visos galimos baigtys, dažnai užrašomos kaip Ω {\displaystyle \Omega } , o rezultatas - ω {\\displaystyle \Omega } .
K: Kas yra rezultatas?
A: Rezultatas yra vieno modelio vykdymo rezultatas.
K: Kam naudojami įvykiai tikimybių erdvėse?
A: Įvykiai naudojami rezultatų grupėms apibūdinti, nes atskiri rezultatai gali būti mažai naudingi praktiškai. Visų tokių įvykių rinkinys vadinamas σ-algebra, kartais užrašomas kaip F {\displaystyle {\mathcal {F}}}.
Klausimas: Kaip kiekvienam įvykiui priskiriamos tikimybės?
A: Tikimybės kiekvienam įvykiui priskiriamos naudojant tikimybinio mato funkciją P.
K: Kas įvedė tikimybių erdvių sąvoką? Atsakymas: Žymus sovietų matematikas Andrejus Kolmogorovas XX a. ketvirtajame dešimtmetyje kartu su kitomis tikimybių aksiomomis įvedė tikimybinių erdvių sąvoką.
