AlegsaOnline.com

Gravitacijos pagreitis g – apibrėžimas, SI vienetas ir Žemės vertė 9,80665 m/s²

Gravitacijos pagreitis g – apibrėžimas, SI vienetas m/s², Žemės standartinė vertė 9,80665 m/s² ir veiksniai nulemiantys jo kitimą

Autorius: Leandro Alegsa

24-08-2025

Pagreitis, kurį objektas įgyja dėl gravitacinės jėgos, vadinamas gravitacijos pagreičiu. Jo SI vienetas yra m/s². Gravitacijos pagreitis yra vektorius, t. y. jis turi ir dydį, ir kryptį. Gravitacijos pagreitis Žemės paviršiuje žymimas raide g. Jo standartinė vertė yra 9,80665 m/s² (32,1740 ft/s²), tačiau tikrasis laisvai krintančio kūno pagreitis kinta priklausomai nuo vietos.

Kaip apskaičiuojamas gravitacijos pagreitis?

Žemės atveju gravitacijos pagreitį galima apytiksliai gauti iš Niutono gravitacijos dėsnio:

g = GM / r²,

kur G yra grav. konstanta (≈ 6,67430·10⁻¹¹ m³·kg⁻¹·s⁻²), M – Žemės masė (~5,97·10²⁴ kg), o r – atstumas iki Žemės centro (≈ 6,371·10⁶ m). Įstatę šias apytiksles reikšmes gauname reikšmes, artimas 9,81 m/s², tačiau tikslesnė standartinė konvencija – 9,80665 m/s² (žymima ir kaip g0 arba „standartinis gravitacijos pagreitis“).

Kodėl g skiriasi priklausomai nuo vietos?

Latitude: dėl Žemės sukimosi ir elipsoidinės formos g yra didesnis prie polių (~9,832 m/s²) ir mažesnis prie pusiaujo (~9,780 m/s²).
Aukštis virš jūros lygio: didėjant aukščiui atstumas iki Žemės centro didėja, tad g mažėja (apytiksliai g(h) ≈ g0·(1 − 2h/R) small h atveju arba naudoti GM/(R+h)² tiksliai).
Žemės sukimosi centrfugalinė jėga sumažina efektyvų pagreitį ypač prie pusiaujo (~0,03–0,04 m/s² skirtumas).
Lokali geologija: tankių uolienų telkiniai ar kiti masių užuomazgos gali sukelti nedidelius anomalijas (kartais keliasdešimt mGal; 1 mGal = 10⁻⁵ m/s²).

Matavimas ir vienetai

SI vienetas: m/s². Gravitacijos laukas taip pat išreiškiamas N/kg (1 N/kg = 1 m/s²).
Geofizikoje dažnai vartojamas gal: 1 gal = 1 cm/s². Todėl standartinis g ≈ 980,665 gal.
Matavimo prietaisai: absoliutūs ir reliatyvūs gravimetrai, palydovinės misijos (pvz., GRACE) naudojamos Žemės masės pasiskirstymo ir pagreičio pokyčių tyrimams.

Praktiniai pastebėjimai ir formulės

Svoris ir masė: kūno svoris W = m·g. Masė m nesikeičia, o svoris priklauso nuo vietos g reikšmės. Pvz., 70 kg žmogaus svoris prie vidutinio g (~9,80665 m/s²) yra ≈ 686,5 N.
Laisvo kritimo formulės: per atstumą s krintančio kūno laikas t be oro pasipriešinimo: s = ½ g t²; t = sqrt(2s/g). Pvz., kritimas per 1 m trunka t ≈ 0,45 s.
Orbitos „sviestumas“: kosmonautai orbitoje jaučiasi „svorio netekę“, nors gravitacija ten vis dar stipri (pvz., ~8,7 m/s² ~ 400 km aukštyje) – jausmas kyla todėl, kad ir laivas, ir astronautai krinta kartu (laisvasis kritimas).

Pritaikymai

Gravitacijos pagreitis svarbus:

inžinerijoje ir statybose (apkrovų skaičiavimai),
balistikoje ir navigacijoje,
geofizikoje (naftos, mineralų paieška, žemės struktūros tyrimai),
meteorologijoje ir okeanografijoje (poveikis srovių ir jūros lygiui),
medicinoje ir biologijoje (tyrimai mikrogravitacijos sąlygomis).

Santrauka: gravitacijos pagreitis Žemės paviršiuje įprastai imamas kaip 9,80665 m/s² (standartinė konvencija), tačiau reali reikšmė priklauso nuo geografinės padėties, aukščio, Žemės formos ir vietinių geologinių sąlygų. Matavimo tikslumas ir pagreičio profilis yra svarbūs tiek mokslo, tiek praktiniuose uždaviniuose.

Kodėl sunkesni daiktai nekrenta greičiau nei lengvesni

Izaokas Niutonas nustatė, kad rezultatinė jėga lygi masės ir pagreičio sandaugai, arba simboliais: F = m a {\displaystyle F=ma} $F=ma$ . Tai galima pertvarkyti taip: a = F m {\displaystyle a={{\frac {F}{m}}}\ } $a={\frac {F}{m}}\$ . Kuo didesnė krintančio objekto masė, tuo didesnė gravitacinės traukos jėga traukia jį į Žemę. Pirmiau pateiktoje lygtyje ši jėga yra F {\displaystyle F} . Tačiau kiek kartų jėga padidėja arba sumažėja, tiek kartų masė padidėja arba sumažėja, o santykis išlieka pastovus. Visais atvejais F m {\displaystyle {\frac {F}{m}}} ${\frac {F}{m}}\$ panaikinama iki vienodo pagreičio, kuris yra maždaug 9,8 m/s² . Tai reiškia, kad nepriklausomai nuo jų masės visi laisvai krintantys objektai greitėja vienodai.

Panagrinėkite šiuos pavyzdžius:

a = 49 N 5 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}\ =9,8\,\mathrm {N/kg} =9,8\,\mathrm {m/s^{2}} } $a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}}$

a = 147 N 15 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}\ =9,8\,\mathrm {N/kg} =9,8\,\mathrm {m/s^{2}} } $a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}}$

Paviršiaus pagreitis

Priklausomai nuo vietos, objektas Žemės paviršiuje krenta su pagreičiu nuo 9,76 iki 9,83 m/s² (nuo 32,0 iki 32,3 pėdų/s² ).

Žemė nėra tiksliai rutulio formos. Ji panaši į "sugniuždytą" rutulį, kurio spindulys ties ekvatoriumi yra šiek tiek didesnis už spindulį ties ašigaliais. Dėl to šiek tiek padidėja gravitacinis pagreitis ašigaliuose (nes esame arti Žemės centro, o gravitacinė jėga priklauso nuo atstumo) ir šiek tiek sumažėja ekvatoriuje. Be to, dėl įcentrinio pagreičio gravitacijos pagreitis ties ekvatoriumi yra šiek tiek mažesnis nei ties ašigaliais. Po žeme esančių uolienų tankio pokyčiai arba netoliese esantys kalnai gali šiek tiek paveikti gravitacinį pagreitį.

Aukštis

Objekto pagreitis kinta priklausomai nuo aukščio. Gravitacinio pagreičio kitimas priklausomai nuo atstumo nuo Žemės centro vyksta pagal atvirkštinio kvadrato dėsnį. Tai reiškia, kad gravitacinis pagreitis atvirkščiai proporcingas atstumo iki Žemės centro kvadratui. Padvigubinus atstumą, gravitacinis pagreitis sumažėja 4 kartus, patrigubinus atstumą, gravitacinis pagreitis sumažėja 9 kartus ir t. t.

gravitacinis pagreitis ∝ 1 atstumas 2 {\displaystyle {\mbox{gravitacinis pagreitis}}} \\propto \ {\frac {1}{{{\mbox{atstumas}}^{2}}}}}} } ${\mbox{gravitational acceleration}}\ \propto \ {\frac {1}{{\mbox{distance}}^{2}}}\$

gravitacinis pagreitis × atstumas 2 = k {\displaystyle {\mbox{gravitacinis pagreitis}} \\ kartus {{\mbox{atstumas}}}^{2}}\ ={k}} ${\mbox{gravitational acceleration}}\ \times {{\mbox{distance}}^{2}}\ ={k}$

Žemės paviršiuje gravitacijos pagreitis yra maždaug 9,8 m/s² (32 pėdų/s² ). Vidutinis atstumas iki Žemės centro yra 6 371 km (3 959 mylios).

k = 9,8 × 6371 2 {\displaystyle {k}={\mbox{9,8}} \ kartus {{\mbox{6371}}^{2}}} ${k}={\mbox{9.8}}\ \times {{\mbox{6371}}^{2}}$

Naudojant konstantą k {\displaystyle k} galime apskaičiuoti gravitacinį pagreitį tam tikrame aukštyje.

gravitacinis pagreitis = k atstumas 2 {\displaystyle {\mbox{gravitacinis pagreitis}} ={\frac {k}{{{\mbox{atstumas}}}^{2}}}}}\ } ${\mbox{gravitational acceleration}}\ ={\frac {k}{{\mbox{distance}}^{2}}}\$

Pavyzdys: Raskite gravitacijos pagreitį 1000 km (620 mylių) aukštyje virš Žemės paviršiaus.

6371 + 1000 = 7371 {\displaystyle 6371+1000=7371} $6371+1000=7371$

∴ Atstumas nuo Žemės centro - 7 371 km.

gravitacinis pagreitis = 9,8 × 6371 2 7371 2 ≈ 7,3 {\displaystyle {\mbox{gravitacinis pagreitis}}} ={\frac {{\mbox{9,8}}} \\ kartus {{\mbox{6371}}^{2}}}}{{{\mbox{7371}}^{2}}}}\\\aprox 7,3} ${\mbox{gravitational acceleration}}\ ={\frac {{\mbox{9.8}}\ \times {{\mbox{6371}}^{2}}}{{\mbox{7371}}^{2}}}\ \approx 7.3$

∴ Pagreitis dėl gravitacijos 1000 km (620 mylių) aukštyje virš Žemės paviršiaus yra 7,3 m/s² (24 pėdų/s² ).

Gravitacinis pagreitis ties Karmano linija - riba tarp Žemės atmosferos ir kosmoso, esančia 100 km (62 mylių) aukštyje, yra tik apie 3 % mažesnis nei jūros lygyje.

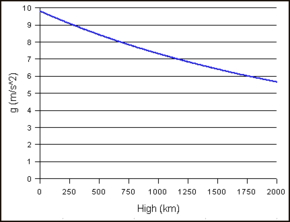
Gravitacinio pagreičio kitimas priklausomai nuo objekto aukščio

Klausimai ir atsakymai

K: Kas yra sunkio jėgos pagreitis?

Atsakymas: Pagreitis dėl gravitacijos - tai pagreitis, kurį objektas įgyja dėl gravitacinės jėgos.

K: Koks yra sunkio jėgos pagreičio SI vienetas?

A: Gravitacijos pagreičio SI vienetas yra m/s2.

K: Ar gravitacijos pagreitis yra skaliaras, ar vektorius?

Atsakymas: Gravitacijos pagreitis yra vektorius, nes jis turi ir dydį, ir kryptį.

K: Koks simbolis naudojamas gravitacijos pagreičiui Žemės paviršiuje išreikšti?

Atsakymas: Žemės paviršiuje gravitacijos pagreičiui išreikšti naudojamas simbolis g.

K: Kokia yra standartinė Žemės paviršiaus sunkio jėgos pagreičio vertė?

A: Standartinė sunkio jėgos pagreičio Žemės paviršiuje vertė yra 9,80665 m/s2 (32,1740 ft/s2).

K: Ar laisvai krintančio kūno tikrasis pagreitis kinta priklausomai nuo vietos?

A: Taip, tikrasis laisvojo kritimo kūno pagreitis kinta priklausomai nuo vietos.

K: Koks yra gravitacijos pagreičio apibrėžimas?

Atsakymas: Gravitacijos pagreitis - tai pagreitis, kurį objektas įgyja dėl gravitacinės jėgos ir kuris žymimas raide g, o jo standartinė vertė Žemės paviršiuje yra 9,80665 m/s2 , nors tikrasis pagreitis gali skirtis priklausomai nuo vietos.