Visatos forma
Visatos formos negalima aptarti kasdieniniais terminais, nes visi terminai turi būti Einšteino reliatyvumo terminai. Todėl Visatos geometrija nėra įprastinė Euklido geometrija, kokia yra mūsų kasdienybėje.
Pagal specialiąją reliatyvumo teoriją neįmanoma pasakyti, ar du skirtingi įvykiai įvyksta tuo pačiu metu, jei tie įvykiai yra atskirti erdvėje. Specialiosios reliatyvumo teorijos požiūriu kalbėti apie "visatos formą (tam tikru laiko momentu)" yra naivu. Dėl vienalaikiškumo reliatyvumo negalime kalbėti apie skirtingus erdvės taškus kaip "esančius tame pačiame laiko taške" ir todėl negalime kalbėti apie "visatos formą laiko taške".
Astrofizikai klausia, ar tam tikras visatos modelis atitinka tai, kas žinoma stebint ir matuojant visatą. Jei stebima visata yra mažesnė už visą visatą (kai kuriuose modeliuose ji yra daug eilių mažesnė ar net be galo maža), stebėjimas apsiriboja visumos dalimi.
Svarstymus apie visatos formą galima suskirstyti į dvi dalis:
- vietinė geometrija, kuri ypač susijusi su visatos kreivumu, ypač stebimoje visatoje, ir
- visuotinė geometrija, susijusi su visos visatos topologija, kurios išmatuoti gali būti neįmanoma.
Stebima visata yra bet kokio visatos modelio tikrinimo pagrindas. Tai sferinis tūris (rutulys), kurio centre yra stebėtojas, nepriklausomai nuo visos visatos formos. Kiekviena visatos vieta turi savo stebimąją visatą, kuri gali sutapti arba nesutapti su ta, kurios centras yra Žemėje.
Naujausi matavimai leido NASA pareikšti: "Dabar mes žinome, kad visata yra plokščia tik su 0,4 % paklaida". Viename iš modelių, FLRW modelyje, šiuo metu populiariausia Visatos forma, kuri, kaip nustatyta, atitinka stebėjimų duomenis, yra begalinės plokštumos modelis. Yra ir kitų modelių, kurie taip pat atitinka duomenis.
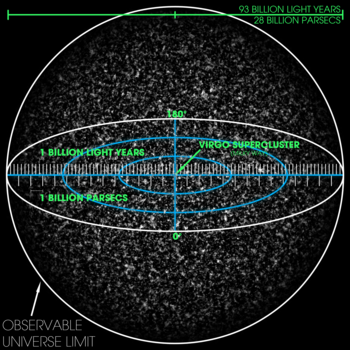
93 milijardų šviesmečių (arba 28 milijardų parsekų) trimatės stebimos visatos vizualizacija. Mastelis toks, kad smulkūs grūdeliai vaizduoja daugybės superklasterių rinkinius. Centre pažymėtas Mergelės superklasteris, kuriame gyvena Pieno kelias, tačiau jis per mažas, kad būtų matomas paveikslėlyje.
Klausimai ir atsakymai
K: Kokia visatos forma, remiantis dabartiniais stebėjimais?
A: Remiantis naujausiais matavimais, NASA teigė, kad visata yra plokščia tik su 0,4 % paklaida.
K: Kaip specialusis reliatyvumas veikia mūsų supratimą apie visatos formą?
A: Dėl vienalaikiškumo reliatyvumo neįmanoma pasakyti, ar du skirtingi įvykiai įvyksta tuo pačiu metu, jei tie įvykiai yra atskirti erdvėje. Tai reiškia, kad negalime kalbėti apie skirtingus erdvės taškus kaip "esančius tame pačiame laiko taške" ir todėl negalime kalbėti apie "visatos formą tam tikru laiko momentu".
Klausimas: Kokią geometriją naudoja astrofizikai, kalbėdami apie Visatos formą?
Atsakymas: Astrofizikai naudoja Einšteino reliatyvumo geometriją aptardami ir tikrindami Visatos aprašymo ir prognozavimo modelius. Jie taip pat atsižvelgia į vietinę geometriją, kuri ypač susijusi su kreivumu, ir į visuotinę geometriją, kuri susijusi su topologija.
Klausimas: Ar kiekviena Visatos vieta yra stebimos Visatos dalis?
Atsakymas: Taip, kiekviena Visatos vieta turi savo stebimą visatą, kuri gali sutapti arba nesutapti su Žemėje esančia visata.
K: Ką reiškia "plokščias", kai kalbama apie modelį, skirtą Visatos aspektams aprašyti ir (arba) prognozuoti?
A: Viename iš modelių, vadinamame FLRW (Friedmann-Lemaître-Robertson-Walker), "plokščias" reiškia begalinį plokščią modelį, kuris, kaip nustatyta, geriausiai atitinka stebėjimo duomenis. Tai reiškia, kad erdvė atrodo vienoda, kad ir kur žiūrėtum, ir šiame modelyje nėra jokių kreivių ar vingių.
Klausimas: Ar yra kitų modelių, kurie, be FLRW begalinio plokščiojo modelio, atitinka stebėjimų duomenis?
A: Taip, be FLRW begalinio plokščio modelio, yra ir kitų modelių, kurie atitinka stebėjimo duomenis.
