Venno diagrama: apibrėžimas, istorija ir taikymai

Sužinokite Venno diagramų apibrėžimą, istoriją ir praktinius taikymus matematikos, logikos, statistikos ir informatikos užduotims — aiškiai, suprantamai ir naudingai.

Venno diagrama - tai diagrama, kuri parodo loginį ryšį tarp rinkinių. Jas 1880–1881 m. išpopuliarino Johnas Vennas ir dabar jos plačiai naudojamos. Venno diagramose aibėms vaizduoti plokštumoje nubrėžiamos uždaros kreivės — dažniausiai apskritimai arba elipsės — kurių sankirtos atitinka aibių bendras dalis. Venno diagramų paprastumas ir vaizdingumas leidžia greitai suprasti sąryšius tarp aibių ir iliustruoti logines bei aibių operacijas.

Pagrindinės sąvokos ir operacijos

Venno diagramose paprastai sutinkamos šios sąvokos:

• Aibė (rinkinis) — vaizduojama viena kreive arba sritimi.
• Visuminė aibė — viskas, kas nagrinėjama (kartais pažymima stačiakampiu fonu).
• Sankirta (intersection) A ∩ B — regionas, kuriame susiduria dvi ar daugiau aibių.
• Unija (union) A ∪ B — visos sritys, priklausančios bent vienai iš aibių.
• Komplementas A^c — viskas, kas priklauso visumai, bet ne aibei A.
• Skirtumas A \ B — ta dalis A, kuri nėra B dalis.
• Disjunktinės aibės — neturinčios bendrų elementų aibės (diagramoje jų kreivės nesikerta).

Pavyzdžiai (skaitymas ir skaičiavimai)

Venno diagramose lengva matyti ir rašyti formules. Pavyzdžiui, dviejų aibių atveju galioja:

• P(A ∪ B) = P(A) + P(B) − P(A ∩ B) — tai dažnai naudojama tikimybių užduotyse.
• A \ B grafiškai atitinka A sritį, iš kurios pašalinta sankirta su B.

Trijų aibių (A, B, C) diagramoje įprastai pažymimos 7 arba 8 atskiros sritys (trijų dvigubų sankirtų sritys, viena trijų aibių sankirta ir trys tik vienos aibės sritys), kas leidžia aiškiai suskaičiuoti elementų pasiskirstymą ir spręsti uždavinius su keliomis sąlygomis.

Trumpa istorija

Panašios idėjos buvo siūlytos ir anksčiau nei Vennas. Panašias idėjas 1712 m. pateikė Christianas Weise (Nucleus Logicoe Wiesianoe) ir 1768 m. Leonhardas Euleris (Laiškai vokiečių princesei). Šią idėją išpopuliarino Johnas Vennas savo knygoje Simbolinė logika, V skyriuje „Diagramatinis vaizdavimas“, 1881 m., kur jis pateikė sistemingą Venn diagramų naudojimą aibių teorijoje ir logikoje.

Venno ir Eulerio diagramų skirtumai

Nors Venno ir Eulerio diagramos atrodo panašiai, jos skiriasi tikslais:

• Venno diagrama vaizduoja visas galimas aibių sankirtas, net jei kai kurios iš jų tuščios; ji naudinga teigti apie visus galimus ryšius tarp aibių.
• Eulerio diagrama rodo tik tas sankirtas, kurios iš tikrųjų egzistuoja; ji paprastai yra aiškesnė, kai tarp aibių nėra visų galimų sąveikų.

Taikymai

Venno diagramų panaudojimas yra labai platus:

• Mokymas ir vizualizacija: pradinių koncepcijų, tokių kaip junginiai, sankirtos ir komplementai, aiškinimas mokykloje.
• Tikimybė ir statistika: sąlyginių ir bendrųjų tikimybių iliustravimas, duomenų pasiskirstymo demonstravimas.
• Logika ir Boolean algebra: loginiai santykiai, taisyklių jungtys ir paprasti įrodymai.
• Informatika ir duomenų bazės: užklausų sąlygų vaizdavimas, duomenų filtravimas, kryžio taškų analizė.
• Lingvistika, medicinos diagnostika, teisė ir verslas: bendrų požymių arba kriterijų nustatymas ir analizė (pvz., simptomų sankirtos pacientų grupėse).
• Infografika ir komunikacija: paprastas būdas perteikti santykius platesnei auditorijai.

Kaip braižyti ir žymėti

Keletas praktinių patarimų:

• Pradėkite nuo visuminės aibės pažymėjimo (pvz., stačiakampis fonas), tada nubrėžkite apskritimus ar elipses kiekvienai aibei.
• Žymėkite aibes raidėmis (A, B, C) ir, jei reikia, skaičiais pažymėkite atskiras sritis, kad būtų lengva nuoroda sprendžiant uždavinius.
• Naudokite spalvas arba užpildymą (shading) paženklinti tam tikras sritis — tai ypač naudinga pristatymuose ir mokomojoje medžiagoje.
• Skaičiavimo uždaviniams aiškiai pažymėkite elementų skaičius arba tikimybes kiekvienoje srityje.

Apribojimai ir išplėtimai

Nors Venno diagramos yra labai naudingos, jos turi ribas: vaizduoti daugiau nei 3–4 aibes aiškiai tampa sudėtinga. Yra specialios konstrukcijos simetriškoms Venn diagramoms kelių aibių atveju, taip pat naudojamos programinės priemonės (pvz., statistikos paketai ar braižymo įrankiai), kurios padeda kurti ir skaičiuoti regionus. Taip pat egzistuoja proporcinės Venn diagramų versijos, kur sričių plotai atitinka aibių dydžius, tačiau jas braižyti reikalauja papildomų skaičiavimų.

Venno diagramų paprastumas ir vaizdingumas daro jas nepakeičiamu įrankiu tiek mokyme, tiek praktikoje — jos padeda aiškiai matyti ryšius, aptikti persidengimus ir pagrįstai priimti sprendimus remiantis vizualizuotais duomenimis.

Pavyzdys

Toliau pateiktame pavyzdyje naudojami du rinkiniai A ir B, kurie čia pavaizduoti spalvotais apskritimais. Oranžiniu apskritimu, A rinkiniu, žymimi visi dvikojai gyvi padarai. Mėlynas apskritimas, rinkinys B, vaizduoja gyvus padarus, kurie gali skraidyti. Kiekvieną atskirą būtybių rūšį galima įsivaizduoti kaip tašką kurioje nors diagramos vietoje. Gyvi padarai, kurie gali ir skraidyti, ir turi dvi kojas, pavyzdžiui, papūgos, yra abiejose aibėse, todėl jie atitinka taškus toje srityje, kur mėlynas ir oranžinis apskritimai persidengia. Toje srityje yra visi tokie ir tik tokie gyvi padarai.

Žmonės ir pingvinai yra dvirankiai, todėl jie yra oranžinės spalvos apskritime, bet kadangi jie negali skraidyti, jie yra kairėje oranžinės spalvos apskritimo dalyje, kuri nesutampa su mėlynos spalvos apskritimu. Uodai turi šešias kojas ir skraido, todėl uodų taškas yra mėlynojo apskritimo dalyje, kuri nesutampa su oranžiniu apskritimu. Būtybės, kurios neturi dviejų kojų ir negali skraidyti (pvz., banginiai ir vorai), būtų vaizduojamos taškais, esančiais už abiejų apskritimų ribų.

Bendra aibių A ir B sritis vadinama A ir B sąjunga, žymima A ∪ B. Šiuo atveju sąjungoje yra visi gyvi padarai, kurie yra arba dvikojai, arba gali skraidyti (arba ir viena, ir kita). A ir B sritis, kurioje abi aibės persidengia, vadinama A ir B sankirta, žymima A ∩ B. Pavyzdžiui, abiejų aibių sankirta nėra tuščia, nes yra taškų, kurie vaizduoja būtybes, esančias ir oranžiniame, ir mėlyname apskritime.

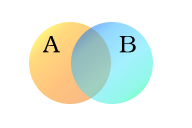
A (dvikojės būtybės) ir B (skraidančios būtybės) rinkiniai

Klausimai ir atsakymai

K: Kas yra Venno diagrama?

K: Kas išpopuliarino Venno diagramas?

K: Kam jos naudojamos?

K: Kas pasiūlė panašias idėjas prieš Džoną Venną?

K: Kada Džonas Vennas paskelbė "Simbolinę logiką"?

K: Kuriame "Simbolinės logikos" skyriuje Džonas Vennas išpopuliarino Venno diagramos idėją?

K: Kaip šios idėjos buvo vaizduojamos prieš išrandant šiuolaikinę V enno diagramos versiją?

Paieška pagal raidę