Cilindras: apibrėžimas, rūšys, paviršiaus plotas ir tūris
Cilindras: sužinokite apibrėžimą, rūšis (apvalus, elipsinis, parabolinis), ir kaip apskaičiuoti paviršiaus plotą bei tūrį – aiškios formulės ir praktiniai pavyzdžiai.
Cilindras — tai geometrinė figūra, sudaroma visų taškų, esančių fiksuotu atstumu nuo tam tikros tiesės atkarpos, vadinamos cilindro ašimi. Kitaip tariant, cilindro paviršių sudaro generatričių (tų pačių krypties tiesių) šeima, kurios kiekvienas taškas yra vienodo atstumo nuo ašies. Tokią figūrą galima įsivaizduoti kaip apskritą arba kitokio kontūro prizmę, kur pagrindai yra lygiagrečios plokštumos, o šoninis paviršius sudarytas iš tiesių, lygiagrečių ašiai. Ir paviršių, ir viduje esantį kietąjį kūną dažnai vadina tiesiog cilindru. Istoriškai cilindro paviršiaus plotas ir tūris buvo skaičiuojami jau senovėje.
Dažniausiai nagrinėjamas specialus atvejis — statmenas (arba stačiakampis) apskritas cilindras, kai pagrindai yra apskritimai. Tokiame cilindre yra du svarbūs parametrai: spindulys r (apskritimo spindulys) ir aukštis h (perpendiculari atstumas tarp pagrindų). Formulės yra paprastos:
- Vieno pagrindo ploto formulė: A = π r².
- Volis: V = A · h = π r² h — tūris lygus pagrindo ploto ir aukščio sandaugai.
- Šoninis (išlinkęs) paviršius: Sš = 2 π r h — tai apskritimo ilgis (2 π r) kartojasi per aukštį.
- Bendras paviršiaus plotas: St = Sš + 2 A = 2 π r h + 2 π r² = 2 π r (r + h).
Svarbu pažymėti, kad tūris nepriklauso nuo to, ar cilindras yra statmenas ar pasviręs — tūris visada lygus pagrindo ploto ir dviejų pagrindų tiesinės atskirties (perpendikulinio aukščio) sandaugai. Tuo tarpu šoninis paviršius pasvirusiame cilindre skaičiuojamas kaip pagrindo perimetro ir generatričių (slantinės) ilgio sandauga — tai gali skirtis nuo 2 π r h, jei generatričių ilgis skiriasi nuo statmens aukščio.
Cilindrų rūšys ir pavyzdžiai:
- Stačiakampis apskritas cilindras (dažniausias mokyklinis atvejis) — pagrindai apskritimai, generatričiai statmenys pagrindų plokštumoms.
- Pasviręs (iškrypęs) cilindras — generatričiai nėra statmeni pagrindams; tūris tas pats, bet šoninis paviršius skaičiuojamas pagal generatričių ilgį.
- Elipsinis cilindras — jei cilindro skerspjūvis yra elipsė, pagrindo plotas A = π a b (a ir b — elipsės puspagrindžiai), todėl tūris V = π a b h.
- Parabolinis ir hiperbolinis cilindrai
- Diferencialinėje geometrijoje cilindras apibrėžiamas plačiau — tai bet koks valdomas paviršius, kurį dengia vieno parametro lygiagrečių tiesių šeima. Tokie cilindrai, kurių skerspjūvis yra elipsė, parabolė arba hiperbolė, vadinami atitinkamai elipsiniu, paraboliniu arba hiperboliniu cilindru. Šie paviršiai gali būti naudojami analizuoti trajektorijoms, architektūrai, inžinerijoje ir kt.
Praktiniai pastebėjimai:
- Matavimo vienetai: tūris matuojamas kubiniais vienetais (pvz., m³), o paviršiaus plotas — kvadratiniais (pvz., m²).
- Tūris nepriklauso nuo to, ar cilindras yra pasviręs — svarbus tik pagrindo plotas ir perpendikulinis aukštis.
- Realioje inžinerijoje cilindrai dažnai naudojami rezervuarams, vamzdžiams, ritinėliams; žinant paviršiaus plotą galima apskaičiuoti reikiamą medžiagą arba dažų kiekį, o tūris svarbus laikymui ar srautų apskaičiavimui.
Trumpai: cilindras — tai paviršius (ar kietasis kūnas), sudarytas lygiagrečių tiesių šeimos aplink ašį; pagrindai gali būti įvairių formų (apskritimai, elipsės ir kt.), todėl bendros formulės tūriui (A pagrindo · h) ir šoninio paviršiaus apibrėžimas pagal pagrindo perimetrą bei generatričių ilgį yra plačiai taikomi.
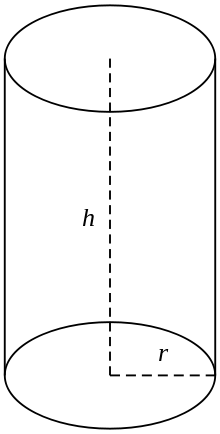
Dešinysis apskritas cilindras
Bendras naudojimas
Įprastai cilindras reiškia baigtinį dešiniojo apskrito cilindro pjūvį, t. y. cilindrą, kurio generuojančios linijos yra statmenos pagrindams, o jo galai yra uždari ir sudaro du apskritus paviršius, kaip parodyta paveikslėlyje (dešinėje). Jei cilindro spindulys r, o ilgis (aukštis) h, tai jo tūris yra lygus:
V = πrh2
o jo paviršiaus plotas yra:
- viršaus plotas (πr2) +
- dugno plotas (πr2) +
- šono plotas (2πrh).
Todėl be viršaus ir apačios (šoninio ploto) paviršiaus plotas yra:
A = 2πrh.
Viršuje ir apačioje paviršiaus plotas yra:
A = 2πr2 + 2πrh = 2πr(r + h).
Tam tikro tūrio cilindro, kurio paviršiaus plotas yra mažiausias, h = 2r. Esant duotam paviršiaus plotui, didžiausio tūrio cilindro h = 2r, t. y. cilindras telpa į kubą (aukštis = skersmuo).
tomas
Dešinysis apskritas cilindras, kurio aukštis yra h vienetų, o pagrindas - r vienetų spindulio, kurio koordinačių ašys parinktos taip, kad pradžia būtų vieno pagrindo centre, o aukštis matuojamas išilgai teigiamos x ašies. Plokščiosios atkarpos, esančios x vienetų atstumu nuo pradžios, plotas yra A(x) kvadratinių vienetų, kur
A ( x ) = π r {\displaystyle2 A(x)=\pi r^{2}}
arba
A ( y ) = π r {\displaystyle2 A(y)=\pi r^{2}}
Tūrio elementas yra dešinysis cilindras, kurio pagrindo plotas Awi kvadratinių vienetų, o storis Δxi vienetų. Taigi, jei V kubinių vienetų yra dešiniojo apvalaus cilindro tūris, pagal Riemanno sumas,
K i l i n d e r o v i s = lim | | Δ → |0 | ∑ i = n 1A ( w i ) Δ i x {\displaystyle \mathrm {Tūris\;iš\;cilindro} =\lim _{||\Delta \to 0|||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x}
= ∫0 h A ( y ) d2 y {\displaystyle =\int _{0}^{h}A(y)^{2}\,dy}
= ∫ 0h π r d 2y {\displaystyle =\int _{0}^{h}\pi r^{2}\,dy}
= π r h 2{\displaystyle =\pi \,r^{2}\,h\,}
Naudojant cilindrines koordinates, tūrį galima apskaičiuoti integruojant per
= ∫ 0h0 ∫ 2π ∫ 0r s d s d ϕ d z {\displaystyle =\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s,\,ds\,d\phi \,dz}
= π r h 2{\displaystyle =\pi \,r^{2}\,h\,}
Cilindrinis pjūvis
Cilindriniai pjūviai - tai cilindrų susikirtimai su plokštumomis. Dešiniojo apskrito cilindro atveju yra keturios galimybės. Plokštuma, liečianti cilindrą, su juo susikerta viena tiesia linija. Lygiagrečiai su savimi judanti plokštuma arba nekerta cilindro, arba kerta jį dviem lygiagrečiomis tiesėmis. Visos kitos plokštumos kerta cilindrą elipse arba, kai jos statmenos cilindro ašiai, apskritimu.
Kiti cilindrų tipai
Elipsinis cilindras, arba cilindroidas, yra keturkampis paviršius, kurio lygtis Dekarto koordinatėse yra tokia:
( x a ) + 2( y b ) =21 . {\displaystyle \left({\frac {x}{a}}}\right)^{2}+\left({\frac {y}{b}}}\right)^{2}=1.}
Ši lygtis skirta elipsiniam cilindrui, kuris yra įprasto apskrito cilindro (a = b) apibendrinimas. Dar bendresnis yra apibendrintasis cilindras: jo skerspjūvis gali būti bet kokia kreivė.
Cilindras yra išsigimęs kvadrikas, nes bent viena jo koordinatė (šiuo atveju z) lygtyje nefigūruoja.
Pasvirusio cilindro viršutinis ir apatinis paviršiai yra pasislinkę vienas nuo kito.
Yra ir kitų neįprastų cilindrų tipų. Tai įsivaizduojami elipsiniai cilindrai:
( x a ) + 2( y b ) =2 - 1{\displaystyle \left({\frac {x}{a}}}\right)^{2}+\left({\frac {y}{b}}}\right)^{2}=-1}
hiperbolinis cilindras:
( x a )2 - ( y b ) = 2{\displaystyle1 \left({\frac {x}{a}}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1}
ir parabolinis cilindras:
x +2 a 2y =0 . {\displaystyle x^{2}+2ay=0.\,}

Elipsinis cilindras

Projektyvinėje geometrijoje cilindras yra tiesiog kūgis, kurio viršūnė yra begalybėje, o tai vizualiai atitinka cilindrą, kuris perspektyvoje atrodo kaip kūgis, nukreiptas į dangų.
Projektyvinė geometrija
Projektyvinėje geometrijoje cilindras yra tiesiog kūgis, kurio viršūnė yra begalybėje.
Tai naudinga apibrėžiant degeneruotus kūgius, kai reikia atsižvelgti į cilindrinius kūgius.
Klausimai ir atsakymai
Klausimas: Kas yra cilindras?
A: Cilindras yra trimatė geometrinė figūra, kurios paviršių sudaro taškai, esantys fiksuotu atstumu nuo tam tikros tiesės atkarpos, vadinamos cilindro ašimi. Jį galima įsivaizduoti kaip apskritą prizmę, o cilindru galima vadinti ir paviršių, ir viduje sukurtą kietąją formą.
Klausimas: Kiek laiko žmonės žino apie cilindrų paviršiaus plotą ir tūrį?
A: Cilindrų paviršiaus plotas ir tūris žinomi nuo seniausių laikų.
K: Kas yra elipsiniai, paraboliniai ir hiperboliniai cilindrai?
A: Elipsiniai, paraboliniai ir hiperboliniai cilindrai - tai cilindrai, kurių skerspjūvis yra atitinkamai elipsė, parabolė arba hiperbolė.
K: Kaip diferencialinėje geometrijoje apibrėžiamas cilindras?
Atsakymas: Diferencialinėje geometrijoje cilindras apibrėžiamas plačiau - kaip valdomas paviršius, kurį dengia vieno parametro lygiagrečiųjų tiesių šeima.
K: Ką reiškia, kad kažkas yra "valdoma"?
Atsakymas: "Valdomas" reiškia, kad ant jo vienaip ar kitaip nubrėžtos tiesės.
K: Ar yra tik viena cilindro rūšis?
Atsakymas: Ne, yra daugybė skirtingų cilindrų tipų, pavyzdžiui, elipsiniai, paraboliniai ir hiperboliniai cilindrai, kurių visi turi skirtingus skerspjūvius.
Ieškoti










