Impedansas
Elektrinė varža - tai grandinės pasipriešinimas srovės ar įtampos pokyčiams.
Yra du pagrindiniai būdai, kaip užrašyti varžą: (žr. 2-ąjį paveikslėlį "kompleksinė impedanso plokštuma")
- su varža "R" (realioji dalis) ir reaktyvumu "X" (įsivaizduojamoji dalis), pavyzdžiui, Z = 1 + 1 j {\displaystyle Z=1+1j}
- su dydžiu ir faze (dydis | Z | {\displaystyle \left\vert Z\right\vert }
ir kampas ∠ θ {\displaystyle \angle \theta }) 
), pavyzdžiui, Z = 1,4 ∠ 45 ∘ {\displaystyle Z=1,4\angle 45^{\circ }} 
(1,4 omo 45 laipsnių kampu)
Impedansas ir varža yra gana panašūs:
Varžos atveju rezistorius priešinasi bet kokiai per jį tekančiai srovei. Kuo didesnė varža, tuo didesnė įtampa reikalinga tam tikrai srovei pasiekti. Formulė yra tokia:
V = R ∗ I {\displaystyle V=R*I}
, kur V - įtampa, R - varža, I - srovė.
Impedanso atveju induktorius priešinasi srovės pokyčiams, o kondensatorius - įtampos pokyčiams.
Pagrindinis skirtumas tarp varžos ir impedanso yra žodis "pokytis", nes pokyčio greitis turi įtakos impedansui. Paprastai "pokytis" išreiškiamas dažniu, t. y. kiek kartų per sekundę srovės ar įtampos kryptis pasikeičia. Formulės yra tokios:
Induktorius: Z = j 2 π f L {\displaystyle Z=j2\pi fL\,} 
Dėl kondensatoriaus: Z = 1 j 2 π f C {\displaystyle Z={\frac {1}{j2\pi fC}}} 
Kur Z yra impedanso simbolis, j yra įsivaizduojamasis skaičius - 1 {\displaystyle {\sqrt {-1}}} 
, π {\displaystyle \pi }
- konstanta pi, f - dažnis, L - induktyvumas, C - talpa. Varžos ir varžos matavimo vienetai yra tie patys - omas su simboliu Ω {\displaystyle \Omega}. 
(didžioji omega).
Kaip nurodyta pirmiau pateiktose formulėse, varža kinta priklausomai nuo dažnio, pavyzdžiui, esant nuliui hercų arba nuolatinei srovei, induktoriaus varža yra lygi nuliui, t. y. trumpoji grandinė, o kondensatoriaus varža yra begalinė, t. y. atvira grandinė. Dauguma signalų yra daugelio sinusinių bangų suma įvairiais dažniais (daugiau informacijos žr. Furjė transformaciją), ir kiekviena iš jų turi skirtingą impedansą.
Panašiai kaip ir varžos atveju, kuo didesnė varža, tuo didesnė įtampa reikalinga tam tikrai srovei pasiekti. Formulė yra tokia:
V = Z ∗ I {\displaystyle V=Z*I}
, kur V - įtampa, Z - varža, o I - srovė.
Fiziniame lygmenyje daug ką supaprastiname:
- varža atsiranda dėl elektronų susidūrimų su atomais rezistorių viduje.
- kondensatoriaus impedanciją lemia elektrinio lauko sukūrimas.
- induktoriaus varžą sukelia magnetinio lauko sukūrimas.
Vienas svarbus skirtumas tarp varžos ir varžos yra tas, kad rezistorius išsklaido energiją, įkaista, o induktorius ir kondensatorius kaupia energiją ir gali ją grąžinti į šaltinį, kai šis sumažėja.
Jei šaltinio, kabelio ir apkrovos varža nėra vienoda, dalis signalo atsispindi atgal į šaltinį, todėl eikvojama energija ir atsiranda trukdžių. Atspindžio santykį galima apskaičiuoti naudojant:
Γ = Z L - Z S Z L + Z S {\displaystyle \Gamma ={Z_{L}-Z_{S} \over Z_{L}+Z_{S}}}}}
, kur Γ {\displaystyle \Gamma } 
(kapitalinė gama) yra atspindžio koeficientas, Z S {\displaystyle Z_{S}}
- šaltinio varža, Z L {\displaystyle Z_{L}}
- apkrovos varža.
Bet kokia terpė, kurioje gali sklisti banga, turi banginį impedansą, net tuščia erdvė (šviesa yra elektromagnetinė banga ir gali sklisti erdvėje) turi maždaug 377 Ω {\displaystyle \Omega } impedansą. .
Signalas iš dalies atsispindi atgal, kai pakinta varža.
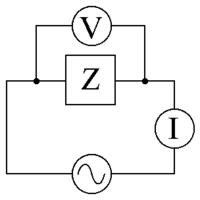
Kintamosios srovės šaltinis, kuriame yra įtampa V {\displaystyle \scriptstyle V} 
per impedanso Z {\displaystyle \scriptstyle Z}, per impedanso Z {\displaystyle \scriptstyle Z}. 
, kuriuo teka srovė I {\displaystyle \scriptstyle I}
.
Kompleksinės varžos plokštumos grafinis vaizdavimas
Fazė
Per rezistorių tiek įtampa, tiek srovė didėja ir mažėja tuo pačiu metu, todėl sakoma, kad jie yra fazėje, tačiau su varža yra kitaip, įtampa pasislenka 1/4 bangos ilgio už srovę kondensatoriuje ir į priekį induktoriuje.
1/4 bangos ilgio paprastai vaizduojamas įsivaizduojamuoju skaičiumi "j", kuris taip pat atitinka 90 laipsnių poslinkį.
Naudojant įsivaizduojamąjį skaičių "j" matematika yra daug paprastesnė, nes jis leidžia apskaičiuoti bendrąją varžą taip pat, kaip tai daroma su rezistoriais, pavyzdžiui, nuoseklusis rezistorius ir varža yra R+Z, o lygiagretusis - (R*Z)/(R+Z).
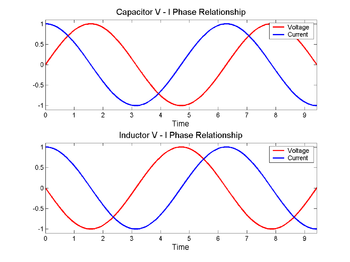
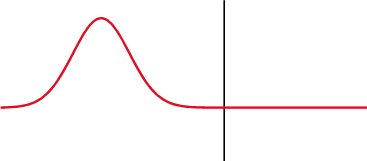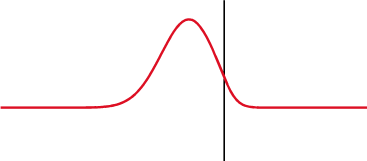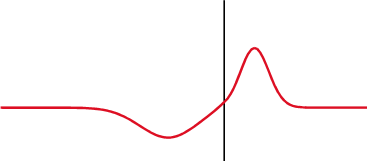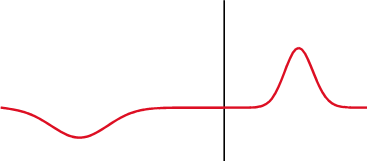
Kondensatoriuje (viršuje) įtampa (raudona) keičiasi po srovės (mėlyna), o induktoriuje (apačioje) - prieš tai. Įtampos ir srovės fazių skirtumas yra 1/4 bangos ilgio.
Klausimai ir atsakymai
K: Kas yra elektrinė varža?
A: Elektrinė varža - tai grandinės pasipriešinimas srovės ar įtampos pokyčiams.
K: Kaip galima užrašyti elektrinę varžą?
A: Elektrinė varža gali būti užrašoma su varža "R" (realioji dalis) ir reaktyvumu "X" (įsivaizduojamoji dalis), taip pat su dydžiu, faze, dydžiu ir kampu.
K: Koks skirtumas tarp varžos ir impedanso?
A: Pagrindinis skirtumas tarp varžos ir impedanso yra žodis "pokytis"; kitaip tariant, pokyčio greitis turi įtakos impedansui. Varža priešinasi bet kokiai per ją tekančiai srovei, tuo tarpu induktorius priešinasi srovės pokyčiams, o kondensatorius - įtampos pokyčiams.
K: Kokios formulės susijusios su varža ir varža?
A: Varža: V=R*I, kur V - įtampa, R - varža, I - srovė; induktoriai: Z=j2πfL; kondensatoriai: Z=1/j2πfC; kur Z - varža, j - įsivaizduojamas skaičius -1 , π - konstanta pi, f - dažnis, L - induktyvumas, C - talpa.
K: Kokie yra fizikiniai varžos ir varžos santykio paaiškinimai?
A: Varža atsiranda dėl elektronų susidūrimo su atomais rezistorių viduje, tuo tarpu induktoriaus impedancija atsiranda dėl elektrinio lauko sukūrimo, o kondensatoriaus - dėl magnetinio lauko sukūrimo. Be to, rezistoriai išsklaido energiją, o induktoriai ir kondensatoriai kaupia energiją, kurią galima grąžinti į šaltinį, kai ji sumažėja.
K: Kaip apskaičiuoti atspindžio koeficientą?
A: Atspindžio koeficientą galima apskaičiuoti naudojant Γ=(ZL-ZS)/(ZL+ZS), kur Γ (didžioji gama) reiškia atspindžio koeficientą; ZS reiškia šaltinio impedanciją; ZL reiškia apkrovos impedanciją.
