Standartinis nuokrypis
Standartinis nuokrypis - tai skaičius, kuris parodo, kaip grupės matavimai skiriasi nuo vidurkio arba tikėtinos vertės. Mažas standartinis nuokrypis reiškia, kad dauguma skaičių yra artimi vidurkiui. Didelis standartinis nuokrypis reiškia, kad skaičiai yra labiau išsibarstę.
Pranešama paklaida paprastai yra du kartus didesnė už standartinį nuokrypį. Mokslininkai paprastai nurodo skaičių standartinį nuokrypį nuo eksperimentų metu gauto skaičiaus vidurkio. Jie dažnai nusprendžia, kad svarbūs tik tie skirtumai, kurie yra didesni nei du ar trys standartinio nuokrypio dydžiai. Standartinis nuokrypis naudingas ir pinigų srityje, kur uždirbtų palūkanų standartinis nuokrypis parodo, kiek vieno asmens uždirbtos palūkanos gali skirtis nuo vidurkio.
Daugeliu atvejų galima išmatuoti tik imtį arba grupės dalį. Tada skaičių, artimą visos grupės standartiniam nuokrypiui, galima rasti pagal šiek tiek kitokią lygtį, vadinamą imties standartiniu nuokrypiu, paaiškintą toliau.
Normaliojo pasiskirstymo (arba varpo kreivės) grafikas. Kiekviena spalvota juosta yra vieno standartinio nuokrypio pločio.
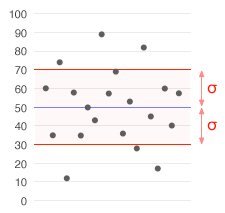
Duomenų rinkinys, kurio vidurkis yra 50 (pavaizduotas mėlynai), o standartinis nuokrypis (σ) - 20.
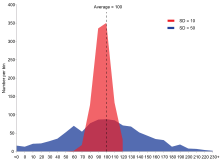
Dviejų imčių populiacijų, turinčių vienodą vidurkį ir skirtingus standartinius nuokrypius, pavyzdys. Raudonosios populiacijos vidurkis yra 100, o SD 10; mėlynosios populiacijos vidurkis yra 100, o SD 50.
Pagrindinis pavyzdys
Panagrinėkime grupę, kurią sudaro šie aštuoni skaičiai:
2 , ,4 ,4 ,4 , 5, , , 5, 7{\displaystyle9 2,\ 4,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9} 
Šių aštuonių skaičių vidurkis yra 5:
2 + +4 +4 + +4 + + 5+ + 5+ 7= 98{\displaystyle5 {\frac {2+4+4+4+4+5+5+7+9}{8}}}=5} 
Norėdami apskaičiuoti populiacijos standartinį nuokrypį, pirmiausia raskite kiekvieno sąrašo skaičiaus skirtumą nuo vidurkio. Tada kiekvieną skirtumą pakelkite kvadratu:
( 2-5 ) =2 ( - 3) =2 (95 - 5) =2 = 02( 04-5 ) =2 ( - 1) = (15 - ) = ( - 25) =2 = 02( 04-5 ) =2 ( - 1) =2 (17 - ) = ( - 5) = 222( 44-5 ) = 2( -1 ) = 2( 19- 5) = = 2= 42{\displaystyle16 {\begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}} 
Tada suraskite šių reikšmių vidurkį (sumą padalykite iš skaičių skaičiaus). Galiausiai išveskite kvadratinę šaknį:
( +9 +1 + +11 + + 0+ + 0+ 4) 16= 8{\displaystyle2 {\sqrt {\frac {(9+1+1+1+1+0+0+0+4+16)}{8}}}=2} 
Atsakymas - populiacijos standartinis nuokrypis. Formulė teisinga tik tuo atveju, jei aštuoni skaičiai, nuo kurių pradėjome, yra visa grupė. Jei jie yra tik atsitiktinai parinkta grupės dalis, tuomet priešpaskutinio žingsnio apačioje (vardiklyje) turėtume naudoti 7 (kuris yra n - 1), o ne 8 (kuris yra n). Tada atsakymas yra imties standartinis nuokrypis. Tai vadinama Besselio pataisa.
Daugiau pavyzdžių
Šiek tiek sunkesnis pavyzdys iš realaus gyvenimo: Vidutinis suaugusių vyrų ūgis Jungtinėse Amerikos Valstijose yra 70 cm, o standartinis nuokrypis - 3 cm. Standartinis 3 colių nuokrypis reiškia, kad daugumos vyrų (maždaug 68 %, jei darytume prielaidą, kad pasiskirstymas normalus) ūgis yra nuo 3 colių aukštesnis iki 3 colių žemesnis už vidutinį (67-73 colių) - tai yra vienas standartinis nuokrypis. Beveik visų vyrų (apie 95 %) ūgis yra nuo 6 cm aukštesnis iki 6 cm žemesnis už vidutinį (64-76 cm) - du standartiniai nuokrypiai. Trys standartiniai nuokrypiai apima visus 99,7 % tiriamos populiacijos imties skaičių. Tai teisinga, jei pasiskirstymas yra normalus (varpo formos).
Jei standartinis nuokrypis būtų lygus nuliui, visi vyrai būtų lygiai 70 cm ūgio. Jei standartinis nuokrypis būtų 20 cm, kai kurie vyrai būtų daug aukštesni arba daug žemesni už vidutinį ūgį, o tipinis diapazonas būtų apie 50-90 cm.
Kitas pavyzdys: kiekvienos iš trijų grupių {0, 0, 14, 14}, {0, 6, 8, 14} ir {6, 6, 8, 8} vidurkis (mean) yra 7. Tačiau jų standartiniai nuokrypiai yra 7, 5 ir 1. Trečiosios grupės standartinis nuokrypis daug mažesnis nei kitų dviejų, nes visi jos skaičiai yra artimi 7. Pagrindinė idėja yra ta, kad standartinis nuokrypis parodo, kaip toli nuo vidurkio yra likusieji skaičiai. Jis turės tuos pačius vienetus kaip ir patys skaičiai. Pavyzdžiui, jei grupė {0, 6, 8, 14} yra keturių brolių grupės amžius metais, tai vidurkis yra 7 metai, o standartinis nuokrypis - 5 metai.
Standartinis nuokrypis gali būti naudojamas kaip neapibrėžtumo matas. Pavyzdžiui, moksle pasikartojančių matavimų grupės standartinis nuokrypis padeda mokslininkams sužinoti, kiek jie yra tikri dėl vidutinio skaičiaus. Sprendžiant, ar eksperimento metu atlikti matavimai sutampa su prognoze, šių matavimų standartinis nuokrypis yra labai svarbus. Jei eksperimentų metu gautas vidutinis skaičius yra per daug nutolęs nuo prognozuojamo skaičiaus (atstumas matuojamas standartiniais nuokrypiais), tuomet tikrinama teorija gali būti neteisinga. Žr. prognozuojamą intervalą.
Taikymo pavyzdžiai
Standartinio nuokrypio reikšmių aibės supratimas padeda sužinoti, kokio didelio skirtumo nuo "vidurkio" (vidurkio) galima tikėtis.
Orai
Kaip paprastą pavyzdį galima pateikti dviejų miestų, esančių šalies gilumoje ir prie vandenyno, vidutinę aukštą paros temperatūrą. Naudinga suprasti, kad netoli vandenyno esančiuose miestuose vidutinė dienos temperatūra yra mažesnė nei miestuose, esančiuose šalies gilumoje. Šių dviejų miestų vidutinė aukšta paros temperatūra gali būti vienoda. Tačiau pakrantės miesto aukštosios paros temperatūros standartinis nuokrypis bus mažesnis nei miesto, esančio šalies gilumoje, standartinis nuokrypis .
Sportas
Kitas būdas tai pamatyti - pažvelgti į sporto komandas. Bet kurioje sporto šakoje yra komandų, kurioms vieni dalykai sekasi, o kiti - ne. Komandos, kurios užima aukščiausias vietas, nepasižymės dideliais gebėjimų skirtumais. Joms gerai sekasi daugumoje kategorijų. Kuo mažesnis jų gebėjimų standartinis nuokrypis kiekvienoje kategorijoje, tuo labiau subalansuotos ir nuoseklesnės jos yra. Tačiau komandos, kurių standartinis nuokrypis didesnis, bus mažiau nuspėjamos. Komandos, kuri paprastai blogai pasirodo daugumoje kategorijų, standartinis nuokrypis bus mažas. Komandos, kuri paprastai yra gera daugumoje kategorijų, standartinis nuokrypis taip pat bus mažas. Tačiau komanda, kurios standartinis nuokrypis didelis, gali būti iš tų, kurios pelno daug taškų (stiprus puolimas), bet taip pat leidžia kitai komandai pelnyti daug taškų (silpna gynyba).
Norint iš anksto sužinoti, kuri komanda laimės, galima pažvelgti į įvairių komandų "statistikos" standartinius nuokrypius. Skaičiai, kurie skiriasi nuo tikėtinų, gali atitikti stipriąsias ir silpnąsias puses ir parodyti, kokios priežastys gali būti svarbiausios, norint sužinoti, kuri komanda laimės.
Lenktynėse matuojamas laikas, per kurį vairuotojas įveikia kiekvieną ratą aplink trasą. Vairuotojas, kurio rato įveikimo laiko standartinis nuokrypis yra mažas, yra pastovesnis už vairuotoją, kurio standartinis nuokrypis yra didesnis. Ši informacija gali būti naudojama siekiant suprasti, kaip vairuotojas gali sutrumpinti rato įveikimo laiką.
Pinigai
Pinigų srityje standartinis nuokrypis gali reikšti riziką, kad kaina (akcijų, obligacijų, nekilnojamojo turto ir kt.) kils arba kris. Jis taip pat gali reikšti riziką, kad kainų grupė kils arba kris (aktyviai valdomi investiciniai fondai, indekso investiciniai fondai arba ETF). Rizika yra viena iš priežasčių, kodėl reikia priimti sprendimus, ką pirkti. Rizika - tai skaičius, kurį žmonės gali naudoti norėdami sužinoti, kiek pinigų jie gali uždirbti arba prarasti. Kai rizika didėja, investicijų grąža gali būti didesnė, nei tikimasi ("plius" standartinis nuokrypis). Tačiau investicija taip pat gali prarasti daugiau pinigų, nei tikėtasi ("minus" standartinis nuokrypis).
Pavyzdžiui, asmuo turėjo pasirinkti vieną iš dviejų akcijų. Akcijos A vidutinė grąža per pastaruosius 20 metų buvo 10 proc., o standartinis nuokrypis - 20 procentinių punktų (pp). Akcijų B vidutinė grąža per pastaruosius 20 metų buvo 12 procentų, tačiau standartinis nuokrypis buvo didesnis - 30 procentinių punktų. Pagalvojęs apie riziką, asmuo gali nuspręsti, kad akcija A yra saugesnis pasirinkimas. Nors jie gali neuždirbti tiek daug pinigų, tačiau tikriausiai ir nepraras daug pinigų. Asmuo gali manyti, kad 2 procentiniais punktais didesnis B akcijos vidurkis nėra vertas papildomo 10 p. p. standartinio nuokrypio (didesnės rizikos arba tikėtinos grąžos neapibrėžtumo).
Normaliai pasiskirsčiusių skaičių taisyklės
Daugumoje matematinių standartinio nuokrypio lygčių daroma prielaida, kad skaičiai pasiskirstę normaliai. Tai reiškia, kad skaičiai pasiskirstę tam tikru būdu abiejose vidurkio pusėse. Normalusis skirstinys dar vadinamas Gauso skirstiniu, nes jį atrado Carlas Friedrichas Gaussas. Jis dažnai vadinamas varpo kreive, nes skaičiai pasiskirsto taip, kad grafike sudaro varpo formą.
Skaičiai nėra normaliai pasiskirstę, jei jie sugrupuoti vienoje ar kitoje vidutinės reikšmės pusėje. Skaičiai gali būti pasiskirstę ir vis tiek būti normaliai pasiskirstę. Standartinis nuokrypis parodo, kaip plačiai skaičiai pasiskirstę.
Tamsiai mėlyna spalva yra mažesnis nei vienas standartinis nuokrypis nuo vidurkio. Normalaus pasiskirstymo atveju tai apima 68,27 proc. skaičių, du standartiniai nuokrypiai nuo vidurkio (vidutinė ir tamsiai mėlyna) apima 95,45 proc. skaičių, trys standartiniai nuokrypiai (šviesiai, vidutiniškai ir tamsiai mėlyna) apima 99,73 proc. skaičių, o keturi standartiniai nuokrypiai - 99,994 proc. skaičių.
Vidutinio (vidurkio) ir standartinio nuokrypio santykis
Duomenų aibės vidurkis ir standartinis nuokrypis paprastai rašomi kartu. Tada žmogus gali suprasti, koks yra vidutinis skaičius ir kaip plačiai grupėje pasiskirstę kiti skaičiai.
Skaičių grupės pasiskirstymą taip pat gali parodyti variacijos koeficientas, kuris yra standartinio nuokrypio ir vidurkio santykis. Tai beasmenis skaičius. Variacijos koeficientas dažnai dauginamas iš 100 % ir rašomas procentais.
Istorija
Terminą standartinis nuokrypis pirmą kartą raštu pavartojo Karlas Pearsonas 1894 m., panaudojęs jį paskaitose. Jis pakeitė ankstesnius tos pačios idėjos pavadinimus: pavyzdžiui, Gausas naudojo vidutinę paklaidą.
Susiję puslapiai
- Tikslumas ir preciziškumas
- Imties dydis
Klausimai ir atsakymai
K: Kas yra standartinis nuokrypis?
A: Standartinis nuokrypis - tai skaičius, naudojamas pasakyti, kaip grupės matavimai skiriasi nuo vidurkio (vidurkio arba tikėtinos vertės).
K: Ką reiškia mažas standartinis nuokrypis?
A: Mažas standartinis nuokrypis reiškia, kad dauguma skaičių yra artimi vidurkiui.
K: Ką reiškia didelis standartinis nuokrypis?
A: Didelis standartinis nuokrypis reiškia, kad skaičiai yra labiau išsibarstę.
K: Kaip standartinis nuokrypis naudojamas piniguose?
A: Pinigų srityje uždirbtų palūkanų standartinis nuokrypis parodo, kiek vieno asmens uždirbtos palūkanos gali skirtis nuo vidurkio.
K: Kada galima matuoti tik dalį grupės?
A: Daugeliu atvejų galima išmatuoti tik imtį arba grupės dalį.
K: Kaip vaizduojamas visos grupės standartinis nuokrypis?
A: Visos grupės standartinis nuokrypis žymimas graikiška raide َ {\displaystyle \sigma } .
K: Kaip vaizduojamas imties standartinis nuokrypis?
A: Imties standartinis nuokrypis žymimas raide s {\displaystyle s} .
