Magnetinis momentas: kas tai, formulė, vienetai ir pritaikymas
Sužinokite, kas yra magnetinis momentas, kaip apskaičiuoti (formulė, vienetai) ir kur pritaikomas — aiškus paaiškinimas, pavyzdžiai ir praktiniai taikymai fizikoje bei technologijose.
Magneto magnetinis momentas - tai dydis, nuo kurio priklauso jėga, kuria magnetas gali veikti elektros srovę, ir sukimo momentas, kuriuo magnetinis laukas jį veikia. Elektros srovės kilpa, strypinis magnetas, elektronas, molekulė ir planeta turi magnetinį momentą.
Tiek magnetinis momentas, tiek magnetinis laukas gali būti laikomi vektoriais, turinčiais dydį ir kryptį. Magnetinio momento kryptis nukreipta nuo magneto pietų į šiaurės ašigalį. Magneto kuriamas magnetinis laukas taip pat proporcingas jo magnetiniam momentui. Tiksliau, magnetinio momento sąvoka paprastai reiškia sistemos magnetinį dipolinį momentą, kuris yra pirmasis bendrojo magnetinio lauko daugiamačio plėtinio narys. Objekto magnetinio lauko dipolinė komponentė yra simetriška jo magnetinio dipolinio momento krypties atžvilgiu ir mažėja kaip atvirkštinis atstumo nuo objekto kubas.
Formulė ir fizikinis paaiškinimas
Magnetinį dipolinį momentą paprastai žymima μ (miu). Pagrindinės formulės:
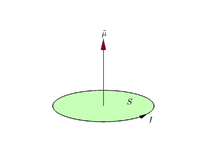
- Elektros srovės kilpai: μ = I·A (vektoriškai μ = I·A n), kur I – srovė, A – kilpos ploto vektorius, kurio kryptis nustatoma dešinės rankos taisykle (ploto vektorius nukreiptas pagal nykščio kryptį, jei pirštai eina srovės kryptimi).
- N ritinių apvijų kilpai: μ = N·I·A.
- Klasikinis ryšys su impulsu (uždara elektroninė orbita): μ = (q/2m)·L, kur q – dalelės krūvis, m – masė, L – orbitalinis momentas.
- Elektrono spinui (kvantinė išraiška): μ_s = -g (e/2m_e) S, kur g – Landé faktorius (elektronui g≈2.0023), e – elektrodo dydis, m_e – elektronų masė, S – spininis momento operatorius.
SI vienetas: ampérų kvadratiniai metrai (A·m²). Tas pats dydis išreiškiamas ir J/T (džuliais per teslą): 1 A·m² = 1 J/T. Cgs sistemoje naudojamas erg/G.
Momenčio poveikis magnetiniam laukui ir energijos sąvokos
- Sukimo momentas (tau): τ = μ × B. Magnetinis momentas patiria sukimo momentą magnetiniame lauke, dėl kurio jis linkęs susilyginti su lauko kryptimi.
- Potencialo energija: U = -μ · B. Sistema turi mažiausią energiją kai μ yra lygiagretus laukui B.
- Nutolusio dipolio laukas: dideliu atstumu B(r) ≈ (μ0/4π) [3(μ·r̂) r̂ - μ]/r³ (SI), t. y. dipolinė lauko dalis mažėja kaip 1/r³.
Skaičiai ir konstantos
- Magnetinis momentas vienos kilpos: tipinė vertė priklauso nuo srovės ir ploto; pvz., I=1 A ir A=1 m² duoda μ=1 A·m².
- Boerio magnetonas: μB = eħ/(2m_e) ≈ 9.274 × 10^−24 A·m². Tai natūralus elektronų magnetinių momentų mastas atominiuose procesuose.
- Žemės magnetinis dipolinis momentas: apie 8 × 10^22 A·m² (orentuotas taip, kad Žemė elgiasi kaip didelis strypinis magnetas).
- Magnetinė konstanta μ0 = 4π·10^−7 T·m/A (SI).
Matrica ir matavimo būdai
Magnetinį momentą galima matuoti keliais būdais:
- Sukimo momentometras: matuoja sukimo momentą, kurį lauke patiria žinoma mėginio magnetizacija.
- SQUID (Superconducting Quantum Interference Device): itin jautrus prietaisas mažiems magnetiniams momentams (atomams, molekulėms).
- Stern–Gerlach eksperimentas: atskiria daleles pagal jų magnetinius momentus (spiną), naudojamas atomų magnetinių momentų tyrimams.
Magnetinio momento pritaikymas ir reikšmė
Magnetinis momentas yra fundamentali savybė, svarbi daugelyje sričių:
- Varikliai ir generatoriai: sukimo momentas nuo magnetinių momentų ir laukų leidžia sukurti mechaninį darbą.
- Atminties ir duomenų saugojimas: magnetinės laikmenos (kietieji diskai, MRAM) naudoja lokalizuotus magnetinius momentus informacijai saugoti.
- MRI (magnetinio rezonanso tomografija): branduolių magnetiniai momentai (spinas) sąveikauja su išoriniais B laukais, leidžia gauti vaizdus ir cheminę informaciją.
- Magnetinė rezonansinė spektroskopija (NMR, ESR): analizuoja molekulinius ir elektroninius magnetinius momentus, svarbi chemijoje ir medžiagų fizikoje.
- Astrofizika ir geofizika: planetų ir žvaigždžių magnetiniai momentai lemia magnetosferas, žvaigždžių vėjo ir kosminių dalelių elgesį.
- Spintronika: elektronų spino magnetiniai momentai naudojami naujos kartos elektronikos įrenginiuose.
Svarbios pastabos ir santrauka
Magnetinis momentas yra vektorinė savybė, kuri apibūdina, kaip stipriai ir kokia kryptimi objektas sąveikauja su magnetiniu lauku. Jis susijęs tiek su srovėmis, tiek su kvantiniais dalelių spinais ir orbitaliniu judesiu. Praktikoje magnetinis momentas lemia sukimo momentą, potencialo energiją lauke ir tolimąjį lauko pasiskirstymą (dipolinę dalį), todėl supratimas ir matavimas yra svarbūs nuo inžinerinių prietaisų iki fundamentalių fizikinių tyrimų.
Du momento apibrėžimai
Vadovėliuose magnetiniams momentams apibrėžti naudojami du vienas kitą papildantys požiūriai. Iki 1930 m. vadovėliuose jie buvo apibrėžiami naudojant magnetinius polius. Naujausiuose vadovėliuose jie apibrėžiami Ampero srovėmis.
Magnetinio poliaus apibrėžimas
Fizikai magnetinių momentų šaltinius medžiagose vaizduoja kaip polius. Šiaurės ir Pietų poliai yra teigiamo ir neigiamo krūvio elektrostatikoje analogija. Panagrinėkime strypinį magnetą, kurio magnetiniai poliai yra vienodo didumo, bet priešingo poliškumo. Kiekvienas polius yra magnetinės jėgos, kuri silpnėja su atstumu, šaltinis. Kadangi magnetiniai poliai visada būna poromis, jų jėgos iš dalies panaikina viena kitą, nes vienas polius traukia, o kitas atstumia. Šis panaikinimas yra didžiausias, kai poliai yra arti vienas kito, t. y. kai strypinis magnetas yra trumpas. Todėl strypinio magneto sukuriama magnetinė jėga tam tikrame erdvės taške priklauso nuo dviejų veiksnių: nuo jo polių stiprumo p {\displaystyle p}

m = p l . {\displaystyle \mathbf {m} =p\mathbf {l} . }
Jis rodo kryptį iš pietų į šiaurės ašigalį. Analogijos su elektriniais dipoliais nereikėtų per daug suprasti, nes magnetiniai dipoliai yra susiję su kampiniu momentu (žr. Magnetinis momentas ir kampinis momentas). Nepaisant to, magnetiniai poliai yra labai naudingi magnetostatiniams skaičiavimams, ypač taikant juos feromagnetais. Praktikai, naudojantys magnetinių polių metodą, paprastai magnetinį lauką vaizduoja iracijos lauku H {\displaystyle \mathbf {H} } 

Srovės kilpos apibrėžimas
Tarkime, kad plokščia uždara kilpa teka elektros srovė I {\displaystyle I}








m = I S . {\displaystyle \mathbf {m} =I\mathbf {S} . }
Pagal susitarimą vektoriaus srities kryptis nustatoma pagal dešinės rankos suėmimo taisyklę (dešinės rankos pirštų sukimas srovės kryptimi aplink kilpą, kai delnas "liečia" išorinį kilpos kraštą, o tiesus nykštys rodo vektoriaus srities, taigi ir magnetinio momento, kryptį).
Jei kilpa nėra plokščia, momentas gaunamas kaip
m = I2 ∫ r × d r . {\displaystyle \mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} . }
Pačiu bendriausiu atveju, kai erdvėje pasiskirsčiusi srovė yra savavališka, tokio pasiskirstymo magnetinį momentą galima rasti pagal šią lygtį:
m = 12∫ r × J d V , {\displaystyle \mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}V,}
kur r {\displaystyle \mathbf {r} }

Pirmiau pateiktą lygtį galima naudoti bet kokio judančių krūvininkų junginio, pavyzdžiui, besisukančio kietojo kūno su krūviu, magnetiniam momentui apskaičiuoti pakeičiant
J = ρ v , {\displaystyle \mathbf {J} =\rho \mathbf {v} , }
kur ρ {\displaystyle \rho }

Pavyzdžiui, magnetinis momentas, kurį sukuria apskritiminiu keliu judantis elektros krūvis, yra
m = q 12r × v {\displaystyle \mathbf {m} ={\frac {1}{2}}\,q\,\mathbf {r} \times \mathbf {v} } 
kur r {\displaystyle \mathbf {r} }


Praktikai, naudojantys srovės kilpos modelį, paprastai magnetinį lauką vaizduoja solenoidiniu lauku B {\displaystyle \mathbf {B} } 

Solenoido magnetinis momentas
Apibendrinta pirmiau minėto srovės kontūro versija yra kelių apsukų ritė arba solenoidas. Jos momentas yra atskirų vijų momentų vektorinė suma. Jei solenoidą sudaro N {\displaystyle N} 
m = N I S . {\displaystyle \mathbf {m} =NI\mathbf {S} . }
.svg.png)
3-D solenoido vaizdas.
Momentas m {\displaystyle \mathbf {m} }


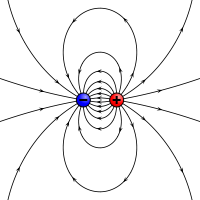
Elektrostatinis magnetinio momento analogas: du priešingi krūviai, kuriuos skiria baigtinis atstumas.
Vienetai
Magnetinio momento vienetas nėra bazinis Tarptautinės vienetų sistemos (SI) vienetas ir gali būti išreikštas daugiau nei vienu būdu. Pavyzdžiui, srovės kilpos apibrėžime plotas matuojamas kvadratiniais metrais, o I {\displaystyle I}


A m = 2N.m T -1 . {\displaystyle \,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}. }
CGS sistemoje yra keli skirtingi elektromagnetinių vienetų rinkiniai, iš kurių pagrindiniai yra ESU, Gauso ir EMU. Tarp jų CGS sistemoje yra du alternatyvūs (nelygiaverčiai) magnetinio dipolinio momento vienetai:
(ESU CGS) 1 statA-cm² = 3,33564095×10-14 (m-A2 arba N.m/T)
ir (dažniau naudojamas)
(EMU CGS ir Gauso CGS) 1 erg/G = 1 abA-cm² = 10-3 (m-A2 arba N.m/T).
Šių dviejų nelygiaverčių CGS vienetų santykis (EMU/ESU) yra lygiai lygus šviesos greičiui laisvoje erdvėje, išreikštam cm/s.
Visos šiame straipsnyje pateiktos formulės yra teisingos SI vienetais, tačiau kitose vienetų sistemose formules gali tekti keisti. Pavyzdžiui, SI vienetais srovės kilpa, kurios srovė I, o plotas A, turi magnetinį momentą I×A (žr. toliau), tačiau Gauso vienetais magnetinis momentas yra I×A/c.
| Kai kurių elementariųjų dalelių vidiniai magnetiniai momentai ir sukiniai | ||
| Dalelės | Magnetinis dipolio momentas SI vienetais (10 −27J/T) | Sukinio kvantinis skaičius (be dimensijos) |
| -9284.764 | 1/2 | |
| protonų | 14.106067 | 1/2 |
| neutronų | -9.66236 | 1/2 |
| miuonai | -44.904478 | 1/2 |
| deuteronas | 4.3307346 | 1 |
| tritonas | 15.046094 | 1/2 |
Magnetinio momento ir įmagnetinimo sąvokų santykį žr.
Klausimai ir atsakymai
K: Kas yra magneto magnetinis momentas?
A: Magneto magnetinis momentas yra dydis, kuris lemia jėgą, kuria magnetas gali veikti elektros srovę, ir sukimo momentą, kuriuo magnetinis laukas jį veikia.
K: Kokie objektai turi magnetinį momentą?
A: Magnetinį momentą turi elektros srovės kilpa, strypinis magnetas, elektronas, molekulė ir planeta.
K: Kaip galima nagrinėti ir magnetinį momentą, ir magnetinį lauką?
A: Ir magnetinis momentas, ir magnetinis laukas gali būti laikomi vektoriais, turinčiais dydį ir kryptį.
K: Kuria kryptimi magnetas nukreipia magnetinį momentą?
Atsakymas: Magnetinio momento kryptis yra nuo magneto pietinio iki šiaurinio poliaus.
K: Koks ryšys tarp magneto magnetinio momento ir magnetinio lauko?
A: Magneto sukuriamas magnetinis laukas yra proporcingas jo magnetiniam momentui.
K: Ką paprastai reiškia sąvoka magnetinis momentas?
A: Tiksliau, magnetinis momentas paprastai reiškia sistemos magnetinį dipolinį momentą, kuris yra pirmasis bendrojo magnetinio lauko daugiamačio plėtinio narys.
K: Kaip objekto magnetinio lauko dipolinė komponentė elgiasi didėjant atstumui nuo objekto?
A: Objekto magnetinio lauko dipolinė komponentė yra simetriška jo magnetinio dipolinio momento krypties atžvilgiu ir mažėja kaip atvirkštinis atstumo iki objekto kubas.
Ieškoti