Taškinė sandauga

Matematikoje taškinė sandauga - tai operacija, kai įvestis yra du vektoriai, o išvestis - skaliarinis skaičius. Grąžinamas skaičius priklauso nuo abiejų vektorių ilgio ir kampo tarp jų. Pavadinimas kilęs iš centruoto taško "-", kuris dažnai naudojamas šiai operacijai žymėti; alternatyvus pavadinimas skaliarinė sandauga pabrėžia skaliarinį (o ne vektorinį) rezultato pobūdį.

Taškinė sandauga (trimatėje erdvėje) skiriasi nuo kryžminės sandaugos, kurios rezultatas yra vektorius.

Apibrėžimas

Dviejų vektorių a = [a₁ , a₂ , ..., a_n ] ir b = [b₁ , b₂ , ..., b_n ] taškinė sandauga apibrėžiama taip:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}} $\mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$

kur Σ reiškia sumavimo užrašą (visų narių suma), o n - vektorinės erdvės matmuo.

2 matmens vektorių [a,b] ir [c,d] taškinė sandauga yra ac + bd. Taip pat 3 matmenyje vektorių [a,b,c] ir [d,e,f] taškinė sandauga yra ad + be + cf. Pavyzdžiui, dviejų trijų matmenų vektorių [1, 3, -5] ir [4, -2, -1] taškinė sandauga yra

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.} $[1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.$

Geometrinė interpretacija

Euklidinėje geometrijoje taškinė sandauga, ilgis ir kampas yra susiję. Vektoriui a taškinė sandauga a - a yra a ilgio kvadratas, arba

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}} ${\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}$

kur ||a|| reiškia a ilgį (dydį). Apskritai, jei b yra kitas vektorius

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\|\cos \theta \,} $\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,$

kur ||a|| ir ||b| žymi a ir b ilgius, o θ - kampą tarp jų.

Šią formulę galima pertvarkyti ir nustatyti kampo tarp dviejų nenulinių vektorių dydį:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta = \arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}}\right\|\left\|{\mathbf {b}}\\right\|}\right)} $\theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)$

Vektorius taip pat galima iš pradžių paversti vienetiniais vektoriais dalijant iš jų dydžio:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}}\right\|}}}} ${\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}$

tada kampas θ yra lygus

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}}cdot {\boldsymbol {\hat {b}}})} $\theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})$

Kadangi 90° kosinusas lygus nuliui, dviejų statmenų vektorių taškinė sandauga visada lygi nuliui. Be to, du vektoriai gali būti laikomi ortogonaliais tada ir tik tada, kai jų taškinė sandauga lygi nuliui ir kai jų abiejų ilgis nenulinis. Ši savybė suteikia paprastą metodą ortogonalumo sąlygai patikrinti.

Kartais šios savybės taip pat naudojamos taškinei sandaugai apibrėžti, ypač 2 ir 3 matmenų atveju; šis apibrėžimas yra lygiavertis pirmiau pateiktam. Aukštesniuose matmenyse formulę galima naudoti kampo sąvokai apibrėžti.

Geometrinės savybės priklauso nuo to, ar pagrindas yra ortonormalus, t. y. sudarytas iš porų statmenų vektorių, kurių ilgis yra vienetas.

Skalarinė projekcija

Jei a ir b ilgis lygus vienetui (t. y. jie yra vienetiniai vektoriai), jų taškinė sandauga yra tiesiog jų tarpusavio kampo kosinusas.

Jei tik b yra vienetinis vektorius, tuomet taškinė sandauga a - b duoda |a| cos(θ), t. y. a projekcijos į b kryptį dydį su minuso ženklu, jei kryptis yra priešinga. Tai vadinama skaliarine a projekcija į b arba skaliarine a komponente b kryptimi (žr. paveikslą). Ši taškinės sandaugos savybė turi keletą naudingų pritaikymų (pvz., žr. kitą skyrių).

Jei nei a, nei b nėra vienetinis vektorius, tuomet, pavyzdžiui, a projekcijos b kryptimi dydis būtų a - (b / |b|), nes vienetinis vektorius b kryptimi yra b / |b|.

Sukimasis

Ortonormaliosios bazės, pagal kurią atvaizduojamas vektorius a, sukimas gaunamas dauginant a iš sukimo matricos R. Ši matricos daugyba yra tik kompaktiškas taškinių sandaugų sekos atvaizdavimas.

Pavyzdžiui, tegul

B₁ = {x, y, z} ir B₂ = {u, v, w} yra dvi skirtingos tos pačios erdvės R³ ortonormaliosios bazės, o B₂ gaunama tiesiog pasukus B₁ ,
a₁ = (a_x , a_y , a_z ) reiškia vektorių a, išreikštą B₁ ,
a₂ = (a_u , a_v , a_w ) vaizduoja tą patį vektorių, išreikštą pasukto pagrindo B₂ terminais,
u₁ , v₁ , w₁ - pasukti baziniai vektoriai u, v, w, išreikšti B₁ .

Tada sukimas iš B₁ į B₂ atliekamas taip:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\{\{\mathbf {w}}_{1}\cdot {\mathbf {a}}}_{1}\end{bmatrix}}}={\begin{bmatrix}a_{u}\a_{v}\a_{w}\end{bmatrix}}}. } ${\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}.$

Atkreipkite dėmesį, kad pasukimo matrica R sudaroma naudojant pasuktus bazinius vektorius u₁ , v₁ , w₁ kaip eilutes, o šie vektoriai yra vienetiniai vektoriai. Pagal apibrėžtį Ra₁ sudaro taškinių sandaugų seka tarp kiekvienos iš trijų R eilučių ir vektoriaus a₁ . Kiekviena iš šių taškinių sandaugų nustato skaliarinę a komponentę pasukto bazinio vektoriaus kryptimi (žr. ankstesnį skyrių).

Jei₁ yra eilutės, o ne stulpelio vektorius, tuomet R turi būti sukti baziniai vektoriai jo stulpeliuose, o po to turi būti padaugintas iš₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. } ${\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.$

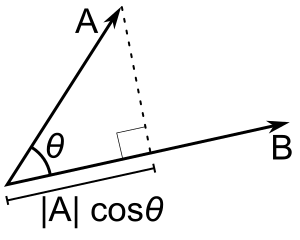
A - B = |A| |B| cos(θ). |A| cos(θ) yra A skaliarinė projekcija į B.

Fizika

Fizikoje dydis yra skaliaras fizikine prasme, t. y. fizikinis dydis, nepriklausantis nuo koordinačių sistemos, išreiškiamas ne tik skaičiumi, bet ir skaitinės vertės ir fizikinio vieneto sandauga. Taškinė sandauga šia prasme taip pat yra skaliaras, išreikštas formule ir nepriklausantis nuo koordinačių sistemos. Pavyzdys:

Mechaninis darbas yra jėgos ir poslinkio vektorių taškinė sandauga.
Magnetinis srautas yra magnetinio lauko ir ploto vektorių taškinė sandauga.
Tūrinis debitas yra skysčio greičio ir ploto vektorių taškinė sandauga.

Savybės

Jei a, b ir c yra realieji vektoriai, o r yra skaliaras, galioja šios savybės.

Taškinė sandauga yra komutacinė:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . } $\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} .$

Taškinė sandauga yra distributyvioji vektorių sudėties atžvilgiu:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . } $\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .$

Taškinė sandauga yra dvinarė:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). } $\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).$

Dauginant iš skaliarinės vertės, taškinė sandauga tenkina:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )} $(c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )$

(paskutinės dvi savybės išplaukia iš pirmųjų dviejų).

Du nenuliniai vektoriai a ir b yra statmeni tada ir tik tada, kai a - b = 0.

Skirtingai nei paprastųjų skaičių daugyba, kai jei ab = ac, tai b visada yra lygus c, nebent a yra nulis, taškinė sandauga nepaklūsta panaikinimo dėsniui:

Jei a - b = a - c ir a ≠ 0, tai pagal skirstinio dėsnį galime užrašyti: a - (b - c) = 0; pirmiau pateiktas rezultatas sako, kad tai reiškia, jog a yra statmena (b - c), todėl (b - c) ≠ 0, taigi b ≠ c.

Jei pagrindas yra ortonormalus, taškinė sandauga nekinta izometriškai keičiant pagrindą: pasukant, atspindint ir derinant, išlaikant fiksuotą pradžią. Pirmiau minėta geometrinė interpretacija remiasi šia savybe. Kitaip tariant, bet kokio matmenų skaičiaus ortonormalioje erdvėje taškinė sandauga yra invariantiška koordinačių transformacijai, pagrįstai ortogonaliąja matrica. Tai atitinka šias dvi sąlygas:

Naujasis pagrindas vėl yra ortonormalus (t. y. jis yra ortonormalus, išreikštas senuoju pagrindu).
Naujieji baziniai vektoriai yra tokio pat ilgio kaip ir senieji (t. y. vieneto ilgio pagal senąjį pagrindą).

Jei a ir b yra funkcijos, tai a - b išvestinė yra a' - b + a - b'

Trigubo produkto išplėtimas

Tai labai naudinga tapatybė (dar vadinama Lagranžo formule), apimanti taškinę ir kryžminę sandaugas. Ji užrašoma taip

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )} $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )$

kurį lengviau įsiminti kaip "BAC minus CAB", nepamirštant, kurie vektoriai yra sujungti taškais. Ši formulė paprastai naudojama siekiant supaprastinti vektorių skaičiavimus fizikoje.

Geometrinės interpretacijos įrodymas

Panagrinėkime elementą R ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + ... + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,} $\mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,$

Pakartotinai pritaikius Pitagoro teoremą, jos ilgis |v|

| v | 2 = v 1 2 + v 2 2 + ... + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,} $|\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,$

Tačiau tai yra tas pats, kas

v ⋅ v = v 1 2 + v 2 2 + ... + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,} $\mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,$

todėl darome išvadą, kad vektoriaus v taškinę sandaugą su pačiu savimi gauname vektoriaus ilgio kvadratą.

1 lema

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,} $\mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,$

Dabar panagrinėkime du vektorius a ir b, einančius iš pradžios, kuriuos skiria kampas θ. Trečiąjį vektorių c galima apibrėžti taip

c = d e f a - b . {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\\\\mathbf {a} -\mathbf {b} .\,} $\mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,$

sudaro trikampį, kurio kraštinės a, b ir c. Pagal kosinuso dėsnį turime

| c | 2 = | a | 2 + | b | 2 - 2 | a | | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $|\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Pagal 1 lemą pakeitę kvadratinių ilgių taškines sandaugas, gauname

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$ (1)

Bet kadangi c ≡ a - b, tai taip pat turime

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} $\mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,$ ,

kuris pagal skirstinio dėsnį išsiplečia iki

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,$ (2)

Sujungę dvi c - c lygtis (1) ir (2), gauname

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Iš abiejų pusių atėmus a - a + b - b ir padalijus iš -2 gaunama

a ⋅ b = | a | | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Q.E.D.

Apibendrinimas

Vidinė sandauga apibendrina taškinę sandaugą abstrakčioms vektorių erdvėms ir paprastai žymima ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle } $\langle \mathbf {a} \,,\mathbf {b} \rangle$ . Dėl geometrinės taškinės sandaugos interpretacijos vektoriaus a norma ||a|| tokioje vidinės sandaugos erdvėje apibrėžiama taip

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={{\sqrt {\langle \\mathbf {a} \,,\mathbf {a} \rangle }}} $\|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}$

taip, kad jis apibendrina ilgį, o kampas θ tarp dviejų vektorių a ir b pagal

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}. } $\cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}.$

Du vektoriai laikomi ortogonališkais, jei jų vidinė sandauga lygi nuliui.

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \angle =0.} $\langle \mathbf {a} \,,\mathbf {b} \rangle =0.$

Vektoriams su kompleksiniais įrašais, naudojant pateiktą taškinės sandaugos apibrėžtį, būtų gaunamos visai kitokios geometrinės savybės. Pavyzdžiui, vektoriaus taškinė sandauga su pačiu savimi gali būti bet koks kompleksinis skaičius ir gali būti lygi nuliui, jei vektorius nėra nulinis vektorius; tai savo ruožtu turėtų rimtų pasekmių tokioms sąvokoms kaip ilgis ir kampas. Daugelį geometrinių savybių galima išgelbėti, tačiau atsisakant simetrinių ir bilinearinių skaliarinės sandaugos savybių, alternatyviai apibrėžiant

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}} $\mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}$

kur b_i yra b _ikompleksinis konjugatas. Tada bet kurio vektoriaus skaliarinė sandauga su pačiu savimi yra neneigiamas realusis skaičius, ir jis yra nenulinis, išskyrus nulinį vektorių. Tačiau ši skaliarinė sandauga nėra tiesinė b (o greičiau konjuguota tiesinė), be to, skalarinė sandauga nėra simetrinė, nes

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}} $\mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}$ .

Vis dėlto tokio tipo skaliarinė sandauga yra gana naudinga ir padeda sukurti hermitinės formos ir bendrųjų vidinių sandaugų erdvių sąvokas.

Frobenijaus vidinė sandauga apibendrina taškinę sandaugą matricoms. Ji apibrėžiama kaip dviejų vienodo dydžio matricų atitinkamų komponenčių sandaugų suma.

Apibendrinimas tenzoriams

Taškinė n eilės tenzoriaus ir m eilės tenzoriaus sandauga yra n+m-2 eilės tenzorius. Taškinė sandauga apskaičiuojama dauginant ir sumuojant abiejų tenzorių vieną indeksą. Jei A {\displaystyle \mathbf {A} } $\mathbf {A}$ ir B {\displaystyle \mathbf {B} } $\mathbf {B}$ yra du tenzoriai, kurių elementų atvaizdavimas A i j ... k ℓ ... {\displaystyle A_{{ij\dots }^{k\ell\dots }} $A_{ij\dots }^{k\ell \dots }$ ir B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}} $B_{mn\dots }^{p{\dots }i}$ yra taškinės sandaugos A ⋅ B {\displaystyle \mathbf {A} elementai. \cdot \mathbf {B} } $\mathbf {A} \cdot \mathbf {B}$ yra duoti taip

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}} $A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}$

Šis apibrėžimas natūraliai redukuojamas į standartinę vektorių taškinę sandaugą, kai jis taikomas vektoriams, ir matricų daugybą, kai jis taikomas matricoms.

Dviguba taškinė sandauga kartais naudojama norint parodyti dviejų indeksų dauginimą ir sumavimą. Dviguba taškinė sandauga tarp dviejų 2 eilės tenzorių yra skaliaras.

Susiję puslapiai

Cauchy-Schwarz nelygybė
Kryžminis produktas
Matricų daugyba
Fizika

Klausimai ir atsakymai

K: Kas matematikoje yra taškinė sandauga?

A: Taškinė sandauga yra veiksmas, kai įvesties metu imami du vektoriai, o išvesties metu grąžinamas skaliarinis skaičius.

K: Nuo ko priklauso taškinė sandauga?

A: Taškinė sandauga priklauso nuo abiejų vektorių ilgio ir kampo tarp jų.

K: Kodėl taškinės sandaugos pavadinimas kilęs iš centruoto taško "-"?

A: Pavadinimas kilęs iš centruoto taško "-", kuris dažnai naudojamas šiai operacijai žymėti.

K: Koks yra alternatyvus taškinės sandaugos pavadinimas?

A: Alternatyvus pavadinimas yra skaliarinė sandauga, kuriuo pabrėžiamas skaliarinis (o ne vektorinis) rezultato pobūdis.

K: Kuo skiriasi taškinė ir kryžminė sandauga trimatėje erdvėje?

A: Taškinės sandaugos rezultatas yra skaliarinis skaičius, o kryžminės sandaugos rezultatas yra vektorius.

K: Kam matematikoje naudojama taškinė sandauga?

A: Taškinė sandauga gali būti naudojama norint nustatyti, ar du vektoriai yra statmeni (sudaro 90 laipsnių kampą), ir projektuojant vieną vektorių į kitą.

K: Ar taškinė sandauga gali būti naudojama didesnių matmenų erdvėse?

A: Taip, taškinę sandaugą galima taikyti didesnių matmenų erdvėse, apibendrinant apibrėžimą.