Harmoninė eilutė (matematika)

Matematikoje harmoninė eilutė yra diverguojanti begalinė eilutė:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}}=1+{\frac {1}{2}}}+{\frac {1}{3}}+{\frac {1}{4}}}+{\frac {1}{5}}}+\cdots } $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Divergentiškumas reiškia, kad pridėjus daugiau narių suma niekada nenustoja didėti. Ji nesiekia vienos baigtinės vertės.

Begalinis reiškia, kad visada galite pridėti kitą terminą. Galutinio serijos nario nėra.

Pavadinimas kilęs iš harmonikos idėjos muzikoje: virpančios stygos obertonų bangos ilgis yra 1/2, 1/3, 1/4 ir t. t. pagrindinės stygos bangos ilgio. Išskyrus pirmąjį narį, kiekvienas eilės narys yra harmoninis vidurkis, lygus priešais jį esančių narių vidurkiui. Frazė harmoninis vidurkis taip pat kilusi iš muzikos.

Istorija

Tai, kad harmoninė eilutė diverguoja, pirmą kartą XIV a. įrodė Nikolas Oresmas, tačiau tai buvo pamiršta. XVII a. įrodymus pateikė Pietro Mengoli, Johannas Bernoulli ir Jacobas Bernoulli.

Harmonines sekas naudojo architektai. Baroko laikotarpiu architektai jas naudojo bažnyčių ir rūmų aukštų planų, aukštų proporcijoms ir architektūrinių detalių santykiams.

Divergencija

Yra keletas gerai žinomų harmoninių eilučių divergencijos įrodymų. Keletas iš jų pateikiami toliau.

Lyginamasis testas

Vienas iš būdų įrodyti divergenciją - palyginti harmoninę eilutę su kita divergentine eilute, kurioje kiekvienas vardiklis pakeičiamas kita didžiąja dviejų galūne:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}}+{\frac {1}{6}}+{\frac {1}{7}}}+{\frac {1}{8}}}+{\frac {1}{9}}}+\cdots \\[12pt]\geq {}&1+{{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{{\frac {1}{\color {red}{\mathbf {8}} }}}+{{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}} ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

Kiekvienas harmoninės eilės narys yra didesnis arba lygus atitinkamam antrosios eilės nariui, todėl harmoninės eilės suma turi būti didesnė arba lygi antrosios eilės sumai. Tačiau antrosios eilės suma yra begalinė:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}}\right)+\left({\frac {1}{4}}}\!+\!{\frac {1}{4}}}\right)+\left({\frac {1}{8}}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}}į dešinę)+\left({\frac {1}{16}}}\!+\!\cdots \!+\!{\frac {1}{16}}} dešinėje)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}} ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

Vadinasi (atlikus palyginimo testą), harmoninių eilučių suma taip pat turi būti begalinė. Tiksliau, pirmiau pateiktas palyginimas įrodo, kad

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

kiekvienam teigiamam sveikam skaičiui $k$ .

Šis įrodymas, kurį apie 1350 m. pasiūlė Nicole'as Oresme'as, laikomas viduramžių matematikos viršūne. Jis ir šiandien yra standartinis matematikos pamokose dėstomas įrodymas.

Integralusis bandymas

Galima įrodyti, kad harmoninė eilutė diverguoja, palyginus jos sumą su netinkamu integralu. Panagrinėkime dešinėje esančiame paveikslėlyje pavaizduotą stačiakampių išsidėstymą. Kiekvienas stačiakampis yra 1 vieneto pločio ir 1/n vienetų aukščio, todėl bendras begalinio skaičiaus stačiakampių plotas yra harmoninės eilės suma:

stačiakampių plotas = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{plotas}}}\\{\text{tiesiakampių}}\{end{array}}=1+{{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}}+\cdots } ${\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Visą plotą po kreive $y =$ 1/x nuo 1 iki begalybės nusako divergentinis netinkamas integralas:

plotas po kreive = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{plotas po}}}\\{\text{krivulė}}}end{array}}}=\int _{1}^{\infty }{\frac {1}{x}}},dx=\infty . } ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

Kadangi visas šis plotas yra stačiakampiuose, bendras stačiakampių plotas taip pat turi būti begalinis. Tai įrodo, kad

∑ n = 1 k 1 n > ∫ 1 k + 1 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}},dx=\ln(k+1). } $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

Šio argumento apibendrinimas vadinamas integraliniu testu.

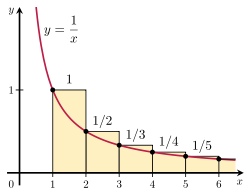
Integralinio testo iliustracija.

Divergencijos greitis

Harmoninė eilutė skiriasi labai lėtai. Pavyzdžiui, pirmųjų 1043 narių suma yra mažesnė nei 100. Taip yra todėl, kad eilės dalinėms sumoms būdingas logaritminis augimas. Konkrečiai,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gama +\varepsilon _{k}\leq (\ln k)+1}} $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

kur $γ$ yra Eulerio-Mascheronio konstanta, o $εk ~$ 1/2k, kuri artėja prie 0, kai $k$ eina į begalybę. Leonhardas Euleris įrodė ir tai, ir tai, kad suma, į kurią įeina tik atvirkštinės pirminių skaičių sumos, taip pat diverguoja, t. y:

∑ p pirminis 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}}+{\frac {1}{17}}}+\cdots =\infty . } $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

Dalinės sumos

Pirmieji trisdešimt harmoninių skaičių
$n$	Harmoninių eilučių dalinė suma, $Hn$
$n$	išreikšta kaip frakcija		dešimtainė	santykinis dydis
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Galutinės dalinės diverguojančių harmoninių eilučių sumos,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}},} $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

vadinami harmoniniais skaičiais.

Skirtumas tarp $Hn$ ir $ln n$ konverguoja prie Eulerio-Mascheronio konstantos. Skirtumas tarp bet kurių dviejų harmoninių skaičių niekada nėra sveikasis skaičius. Nė vienas harmoninis skaičius nėra sveikasis skaičius, išskyrus $H1 = 1$ .

Susijusios serijos

Kintamosios harmoninės eilės

Serija

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}}=1-{\frac {1}{2}}}+{\frac {1}{3}}}-{\frac {1}{4}}}+{\frac {1}{5}}}-\cdots } $\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots$

vadinama kintamąja harmonine eilute. Ši eilutė konverguoja pagal kintamosios eilės testą. Visų pirma, suma yra lygi natūraliojo logaritmo 2 vertei:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.} $1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$

Nors kintamoji harmoninė eilutė yra sąlygiškai konverguojanti, ji nėra absoliučiai konverguojanti: jei eilutės nariai sistemingai pertvarkomi, paprastai suma tampa kitokia ir, priklausomai nuo pertvarkymo, galbūt net begalinė.

Kintamosios harmoninės eilės formulė yra Merkatoriaus eilės, Tayloro natūraliojo logaritmo eilės, specialus atvejis.

Susijusią eilutę galima išvesti iš arktangento Teiloro eilės:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}}{2n+1}}}=1-{\frac {1}{3}}+{\frac {1}{5}}}-{\frac {1}{7}}}+\cdots ={\frac {\pi }{4}}. } $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

Tai vadinama Leibnico eilute.

Bendrosios harmoninės serijos

Bendroji harmoninė eilutė yra tokios formos

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},} $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

kur $a \neq 0$ ir $b$ yra realieji skaičiai, o b/a nėra nulis arba neigiamas sveikasis skaičius.

Atlikus ribinio palyginimo su harmoninėmis eilutėmis testą, visos bendrosios harmoninės eilutės taip pat skiriasi.

$p serijos$

Harmoninių eilučių apibendrinimas yra $p eilutė$ (arba hiperharmoninė eilutė), apibrėžiama taip

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

Kai $p = 1, p- eilutė$ yra harmoninė eilutė, kuri diverguoja. Arba integralinis testas, arba Kaušio kondensacijos testas rodo, kad $p eilutė$ konverguoja visiems $p > 1 (tokiu$ atveju ji vadinama perharmonine eilute) ir diverguoja visiems p $\leq 1.$ Jei $p > 1,$ tai p eilučių suma yra ζ( $p), t. y.$ Rymano zeta funkcija, įvertinta ties p.

Problema, kaip rasti sumą, kai $p = 2,$ vadinama Bazelio problema; Leonhardas Euleris parodė, kad ji yra $π2/6$ . Suma $p = 3$ vadinama Apyrio konstanta, nes Rodžeris Apyris įrodė, kad tai iracionalusis skaičius.

ln serija

Su $p eilute$ susijusi ln eilutė, apibrėžiama taip

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}} $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

bet kuriam teigiamam realiajam skaičiui $p.$ Tai galima įrodyti integraliniu bandymu, nes $p \leq 1$ atveju ji diverguoja, bet $p > 1$ atveju konverguoja.

$φ serijos$

Bet kokiai išgaubtai realiajai funkcijai $φ$ , tokiai, kad

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}}\right)}{\varphi (u)}}<{\frac {1}{2}},}} $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

serija

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}}\right)} $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

yra konverguojantis. ^[]

Atsitiktinės harmoninės serijos

Atsitiktinė harmoninė eilutė

∑ n = 1 ∞ s n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},} $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

kur $sn$ yra nepriklausomi, vienodai pasiskirstę atsitiktiniai kintamieji, įgyjantys reikšmes +1 ir -1 su vienoda tikimybe 1/2, yra gerai žinomas tikimybių teorijos pavyzdys, kai atsitiktinių kintamųjų eilutė konverguoja su tikimybe 1. Šis konvergavimo faktas yra paprasta Kolmogorovo trijų eilučių teoremos arba glaudžiai susijusios Kolmogorovo maksimalios nelygybės pasekmė. Byronas Schmulandas iš Albertos universiteto toliau nagrinėjo atsitiktinių harmoninių eilučių savybes ir parodė, kad konverguojanti eilutė yra atsitiktinis kintamasis, pasižymintis kai kuriomis įdomiomis savybėmis. Visų pirma šio atsitiktinio kintamojo tikimybės tankio funkcija, įvertinta esant +2 arba -2, įgyja reikšmę 0,12499999999999999999999999999999764..., kuri nuo 1/8 skiriasi mažiau nei 10-42. Šmulando straipsnyje paaiškinama, kodėl ši tikimybė yra tokia artima 1/8, bet ne visai lygi jai. Tikslią šios tikimybės vertę nusako begalinės kosinuso sandaugos integralas $C2,$ padalytas iš $π$ .

Išsemtos harmoninių eilės

Galima įrodyti, kad išskaidyta harmoninė eilutė, iš kurios pašalinami visi nariai, kurių vardiklyje bet kur yra skaitmuo 9, konverguoja ir jos vertė yra mažesnė už 80. Tiesą sakant, kai pašalinami visi nariai, kuriuose yra bet kuri konkreti skaitmenų eilutė (bet kuriame pagrinde), eilutė konverguoja.

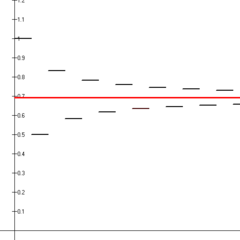
Parodyta keturiolika pirmųjų kintamųjų harmoninių eilučių dalinių sumų (juodos linijos atkarpos), konverguojančių prie natūraliojo logaritmo 2 (raudona linija).

Programos

Harmoninė eilutė gali būti nelogiška. Taip yra todėl, kad tai yra divergentinė eilutė, nors jos nariai mažėja ir artėja prie nulio. Harmoninės eilutės divergencija yra kai kurių paradoksų šaltinis.

"Kirminas ant gumytės". Tarkime, kad kirminas šliaužia be galo elastinga vieno metro ilgio gumine juosta tuo pačiu metu, kai ši juosta yra tolygiai ištempta. Jei sliekas per minutę nueina 1 centimetrą, o juosta per minutę išsitempia 1 metrą, ar sliekas kada nors pasieks gumytės galą? Atsakymas, priešingai nei įprasta, yra "taip", nes po $n$ minučių sliekas įveiks tokį atstumą, kad jo nueito kelio ir viso gumytės ilgio santykis bus

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}. } ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Kadangi, didėjant $n$ , eilutė darosi vis didesnė, galiausiai šis santykis turi viršyti 1, o tai reiškia, kad kirminas pasiekia gumytės galą. Tačiau $n$ reikšmė, kuriai esant tai įvyksta, turi būti labai didelė: maždaug e100, t. y. skaičius, viršijantis 1043 minutes (1037 metus). Nors harmoninė eilutė ir skiriasi, tačiau tai vyksta labai lėtai.

Džipo uždavinyje klausiama, kiek iš viso degalų reikia, kad ribotos talpos automobilis įveiktų dykumą, pakeliui palikdamas degalų lašelius. Atstumas, kurį automobilis gali nuvažiuoti su tam tikru degalų kiekiu, yra susijęs su harmoninių eilučių dalinėmis sumomis, kurios auga logaritmiškai. Taigi degalų poreikis didėja eksponentiškai, didėjant norimam atstumui.

Blokų sudėjimo problema: turint vienodų domino kaladėlių rinkinį, galima jas sudėti prie stalo krašto taip, kad jos kabotų virš stalo krašto ir nenukristų. Priešingas intuicijai rezultatas yra tas, kad juos galima sukrauti taip, kad iškyša būtų tokia didelė, kokios tik norite. Tai yra, jei domino kauliukų yra pakankamai.

Plaukikas, kuris plaukia greičiau kiekvieną kartą, kai paliečia baseino sienelę. Plaukikas pradeda plaukti per 10 m ilgio baseiną 2 m/s greičiu, o kaskart plaukdamas dar 2 m/s greičiu. Teoriškai plaukiko greitis yra neribotas, tačiau norint pasiekti tokį greitį, reikia labai daug kartų perplaukti baseiną; pavyzdžiui, kad pasiektų šviesos greitį (neatsižvelgiant į specialųjį reliatyvumą), plaukikas turi perplaukti baseiną 150 milijonų kartų. Priešingai šiam dideliam skaičiui, laikas, kurio reikia tam tikram greičiui pasiekti, priklauso nuo eilučių sumos bet kuriuo konkrečiu baseino kirtimų skaičiumi:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}. } ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Apskaičiavus sumą paaiškėja, kad šviesos greičiui pasiekti reikia tik 97 sekundžių.

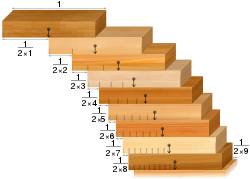
Blokų sudėjimo problema: blokai, išdėstyti pagal harmoninę eilutę, jungia bet kokio pločio skeveldras.

Susiję puslapiai

Harmoninė progresija
Abipusių sumų sąrašas

Klausimai ir atsakymai

K: Kas yra harmonijos serija?

Atsakymas: Harmoninė eilutė yra begalinė divergentinė eilutė, kurioje kiekvienas narys lygus 1, padalytam iš jo vietos sekoje.

K: Ką reiškia, kad eilutė yra divergentiška?

Atsakymas: Divergentinė reiškia, kad, pridedant daugiau narių, suma niekada nenustoja didėti ir nesiekia vienos baigtinės vertės.

K: Ką reiškia, kai eilutė yra begalinė?

A: Begalinė reiškia, kad visada galima pridėti dar vieną narį ir kad eilutė neturi galutinio nario.

K: Iš kur kilo šios serijos pavadinimas?

Atsakymas: Šios serijos pavadinimas kilo iš harmonikų idėjos muzikoje, kai obertonų bangos ilgis yra 1/2, 1/3, 1/4 ir t. t. stygos pagrindinės bangos ilgio.

K: Ką reiškia harmoninė?

A: Harmoninis vidurkis yra tada, kai kiekvienas sekos narys yra lygus gretimų narių harmoniniam vidurkiui. Ši frazė taip pat kilusi iš muzikos.

K: Kaip apskaičiuoti kiekvieną šios sekos narį?

A: Kiekvieną šios sekos narį galima apskaičiuoti padalijus vienetą iš jo padėties sekoje (1/n).